
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интеграл Лебега для простых функций. Интеграл Лебега для произвольных функций. Интегрируемость измеримых ограниченных функцийСодержание книги
Поиск на нашем сайте
1. Интеграл Лебега для простых функций
Пусть
назовем Определение. Интегралом Лебега
Для
Корректность определения интеграла (независимость от выбора представления Лемма 7.1. Если
Доказательство. Вследствие аддитивности
Поэтому достаточно установить, что от записи
Индукция по
Функция
Лемма доказана. Из определения интеграла легко вытекает следующая лемма, устанавливающая его свойства. Лемма 7.2. Пусть 1) 2) 3) если
4) для любых попарно непересекающихся множеств
5)
2. Интеграл Лебега для произвольных функций
В дальнейшем будем рассматривать Определение. Функция 1) 2) В случае выполнения этих условий
Интеграл (7.4) называют абстрактным интегралом Лебега (по мере Проверим корректность определения интеграла (7.4). Лемма 7.3. В (7.4) предел существует. Доказательство. Существование предела следует из фундаментальности последовательности
Лемма 7.4. Если последовательность
Доказательство. Пусть
Для
Итак, для Лемма 7.5. Интеграл (7.4) не зависит от выбора последовательности Доказательство. Пусть
Для
Следовательно, по лемме 7.4
Лемма доказана. Интеграл по множеству
3. Интегрируемость измеримых ограниченных функций
Теорема 7.1. Пусть Доказательство. В случае ограниченной измеримой функции
Следствие 7.1. Пусть Утверждение следует из теоремы 7.1, если перейти к пространству с мерой Теорема 7.2. Если функция
Доказательство. Пусть Пусть
Тогда для
Теорема доказана.
ЛЕКЦИЯ 11
|
||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.40.53 (0.006 с.) |

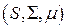 — пространство с полной
— пространство с полной  -конечной мерой. Простую функцию
-конечной мерой. Простую функцию 
 (7.1)
(7.1) -простой, если
-простой, если  ,
,  .
. -простой функции
-простой функции 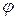 (7.1) на
(7.1) на  называется число
называется число .
. интеграл от
интеграл от  есть величина
есть величина .
. —
—  -простая функция, то
-простая функция, то .
. , утверждение очевидно, если каждое из семейств
, утверждение очевидно, если каждое из семейств  ,
,  состоит из попарно непересекающихся множеств. Если
состоит из попарно непересекающихся множеств. Если  , то
, то  на
на  . Отсюда, вследствие аддитивности меры
. Отсюда, вследствие аддитивности меры  ,
,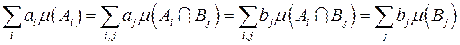 .
. можно перейти к
можно перейти к  , где
, где  — конечное семейство попарно непересекающихся множеств из
— конечное семейство попарно непересекающихся множеств из  , и при этом
, и при этом .
. . Для
. Для  высказывание верно. Пусть оно верно для
высказывание верно. Пусть оно верно для 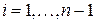 . Докажем его для
. Докажем его для  . По индуктивному предположению
. По индуктивному предположению

 —
—  -простые функции,
-простые функции, 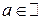 . Тогда
. Тогда ,
, ,
, ,
,  , то
, то ,
,
 ,
, .
.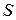
 ,
,  -п.в. конечная на
-п.в. конечная на  -простых функций
-простых функций  , что
, что для
для  , (7.2)
, (7.2) . (7.3)
. (7.3) . (7.4)
. (7.4) .
. :
: .
. -простых функций
-простых функций  .
. . Существует такой номер
. Существует такой номер  , что для всех
, что для всех  ,
,  . Выберем
. Выберем  ,
,  ,
,  . Очевидно, что для
. Очевидно, что для 
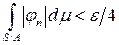 . Если
. Если  , то по теореме 6.1, найдется такое
, то по теореме 6.1, найдется такое  , что
, что  и на
и на 
 равномерно сходится к нулю. Возьмем такое
равномерно сходится к нулю. Возьмем такое  , что при
, что при  ,
,  . Пусть
. Пусть  ;
; . (7.5)
. (7.5) первый интеграл в правой части (7.5) меньше
первый интеграл в правой части (7.5) меньше  . Для другого интеграла при достаточно малом
. Для другого интеграла при достаточно малом 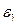

 . Лемма доказана.
. Лемма доказана. и
и  — две последовательности
— две последовательности  ,
,  выбрано так, что
выбрано так, что .
.
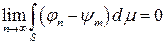 , поэтому
, поэтому 
 .
.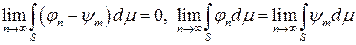 .
. определяем соотношением
определяем соотношением .
.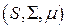 — пространство с полной конечной мерой. Если
— пространство с полной конечной мерой. Если  — измеримая ограниченная на
— измеримая ограниченная на  по следствию 5.2 существует последовательность
по следствию 5.2 существует последовательность  , равномерно сходящаяся к
, равномерно сходящаяся к  .
. — измеримое множество конечной меры на пространстве с полной мерой
— измеримое множество конечной меры на пространстве с полной мерой  , то f интегрируема на
, то f интегрируема на  .
. .
. . Если последовательность
. Если последовательность  -простых функций
-простых функций  найдется
найдется  такое, что для всех
такое, что для всех 
 .
. достаточно рассмотреть последовательность
достаточно рассмотреть последовательность  где
где  ,
,  такое, что для
такое, что для 
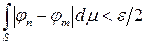 . Из интегрируемости
. Из интегрируемости  на
на  существует
существует  такое, что
такое, что .
. .
.


