
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двухатомная молекула как жесткий ротатор.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одной из самых простых моделей двухатомной молекулы является модель жесткого ротатора:
где Используя уравнение Шредингера, можно показать, что разрешенные уровни вращательной энергии жесткой двухатомной молекулы даются выражением
Энергия молекулы, выраженная в см-1, называется термом:
Или сокращенно
где
Ясно, что при J=0 eJ = 0. Значению J=1 соответствует энергия e1 =2B и т.д. Формально можно продолжать вычисления eJ до бесконечности, и величина этой энергии будет все время возрастать. В действительности же конечно наступает такой момент, когда центробежная сила в быстровращающейся молекуле превысит силу связи, и молекула разрушится, но при обычных температурах до этого дело не доходит.
Для рассмотрения спектра важны не сами энергии уровней, а их разности. Пусть J=0, т.е. молекула находится в основном вращательном состоянии. Тогда, поглощая падающее на нее излучение, молекула может перейти в возбужденное вращательное состояние J=1. Поглощенная при этом энергия равна
Волновое число поглощенного при этом кванта излучения в соответствии с (4.4) n01 = Озвучивается это следующим образом: волновое число спектральной линии равно разности двух термов. Объединяя эти две формулы, получим
Иными словами, линия поглощения появится при 2B (см-1). Может ли произойти переход 0 ®2? Нет – такой переход запрещен правилами отбора. Из уравнения Шредингера следует, что для рассматриваемой молекулы имеют место лишь те переходы, для которых соблюдено: DJ=±1 правила отбора (4.13) Т.е. для жесткого ротатора разрешены переходы только между соседними уровнями. Все остальные переходы запрещены. В общем случае для перехода из состояния J в состояние J+1 имеем:
или
или сокращенно
Такое “ступеньчатое” возрастание энергии вращательных переходов приводит к тому, что спектр поглощения состоит из линий при 2В, 4B, 6B…(см-1):
Спектр излучения будет идентичен и соответствует тем же стрелкам, но только сверху вниз.
Нежесткий ротатор. Спектральные линии в спектре жесткого ротатора должны отстоять друг от друга на расстояние 2B. Однако в реальных спектрах расстояния между соседними линиями, а, следовательно, и эффективные значения B монотонно уменьшаются с ростом J. Причина этого уменьшения заключается в том, что с ростом скорости вращения двухатомной молекулы (т.е. с увеличением J) увеличивается центробежная сила, растягивающая связь и приводящая к увеличению ее длины. Таким образом, допущение о жесткости связи в модели жесткого ротатора является всего лишь приближенным: в действительности все связи до некоторых пределов упруги (см. § 4.5.2). Остановимся кратко на двух следствиях этого свойства химических связей. Во-первых, если связь упруга, молекула может обладать колебательной энергией – энергией периодического растяжения и сжатия связи с определенной частотой, зависящей от масс атомов и от упругости (или силовой постоянной) связи. Ясно, что зависимость B от J должна определяться этой силовой постоянной: чем слабее связь, тем сильнее она деформируется под действием центробежных сил. Вторым следствием упругости связи является то, что при колебаниях величины r и B меняются. При вращении за время одного оборота успевают произойти сотни колебаний связи, и, следовательно, измеренная микроволновыми методами величина r является усредненной. Из определения B следует
Для реальной связи r > re. Поэтому приходится определять несколько наборов значений B и r. Равновесному расстоянию между ядрами re соответствует вращательная постоянная Be – жесткая связь – модель жесткого ротатора. Основное колебательное состояние характеризуется средним межъядерным расстоянием ro, которому соответствует вращательная постоянная Bo. В общем случае, если двухатомная молекула обладает колебательной энергией Ev, то она будет характеризоваться соответствующими значениями rv и Bv (v – колебательное квантовое число). Иногда можно пренебречь малыми различиями между Be, Bo и Bv. Далее в настоящем параграфе мы сделаем это и будем обозначать вращательную постоянную просто B.
Из уравнения Шредингера для двухатомной молекулы как нежесткого ротатора разрешены следующие энергетические состояния (термы): eJ = B•J•(J+1) - D•J2•(J+1)2 где D – постоянная центробежного растяжения. Значение D меньше значения B на несколько порядков, и поэтому при малых J поправочный член D•J2•(J+1)2 можно не учитывать, но при J>10 центробежное растяжение сказывается сильно и его необходимо учитывать. На рис. На стр.38 схематически изображено понижение уровней вращательной энергии при переходе от жестких к нежестким молекулам, а также вызванное этим изменение спектров. Отметим, что, по прежнему, правила отбора DJ = ± 1. Выражение для волнового числа спектральных линий nJ = eJ+1 - eJ = B(J+1)(J+2) – D(J+1)2(J+2)2 – BJ(J+1) + DJ2(J+1)2 = = 2B(J+1) – 4D(J+1)3 (см-1) Из этого аналитического выражения видно, что спектр упругого ротатора похож на спектр жесткого ротатора, за исключением того, что в нем каждая линия несколько смещена в область низких частот, причем смещение возрастает пропорционально (J+1)3:
Э нергетические уровни Жесткий ротатор Упругий ротатор
Спектры
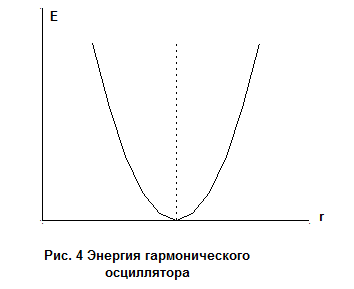
Колебательные состояния. Гармонический осциллятор.
где f-сила упругости, k-силовая постоянная, r - межъядерное расстояние.
Упругая связь, подобно пружине, имеет определенную частоту колебаний, зависящую от массы системы и силовой постоянной, но не от величины деформации:
или
Разрешенные уровни колебательной энергии могут быть найдены из уравнения Шредингера для гармонического осциллятора
или
Отсюда видно, что наименьшая колебательная энергия при v = 0 равна
или
это означает, что колебательная энергия двухатомной (а в действительности и любой другой) молекулы никогда не может равняться нулю, т.е. атомы никогда не могут быть полностью неподвижны относительно друг друга. Наличие нулевой энергии является отражением основного различия между квантово-механическим и классическим описаниями молекулярных колебаний. Согласно классической механике, молекула может перестать колебаться вообще, в то время как квантовая механика настаивает на том, что какие-то колебания всегда должны иметь место. Существование нулевых колебаний подтверждено экспериментально. Значения энергии, вычисленные по формуле (4.15) приведены на рис.5.
Dv = ±1 (4.17)
К этому добавляется условие, что при колебании должен изменяться дипольный момент молекулы (см. «Спектральные области»). Следовательно, колебательные спектры могут наблюдаться только для гетероядерных двухатомных молекул, т.к. гомоядерные молекулы не имеют электрического дипольного момента.
Используя правила отбора, найдем волновые числа спектральных линий гармонического осциллятора:
Мы получили, что волновое число спектральной линии не зависит от v и всегда равно частоте колебаний. Этот простой результат очевиден из рис.5 – так как колебательные уровни гармонического осциллятора эквидистантны, то переходы между любыми соседними уровнями должны приводить к одинаковому изменению энергии. Следовательно, спектр гармонического осциллятора состоит всего из одной спектральной линии.
Ангармонический осциллятор. Реальные молекулы не являются строго гармоническими осцилляторами: реальные связи хотя и упруги, но закон Гука точно не выполняется. Если, например, достаточно сильно растягивать связь, то она, в конце концов, разорвется и молекула диссоциирует на атомы. Для небольших сжатий и растяжений (до 10% длины связи) связь еще можно считать совершенно упругой (то есть подчиняющейся закону Гука), для бóльших же амплитуд энергетическая зависимость становится более сложной, чем парабола. На рис.6 схематически представлена энергетическая зависимость двухатомной молекулы.
Так как кривая Морзе слева от re идет круче, чем парабола, а слева от re – положе, то отсюда вытекает, что реальная химическая связь легче растягивается, чем сжимается.
Зависимость на рис.6 описывается эмпирической формулой - потенциалом Морзе где b - постоянная, характерная для данной молекулы, De - энергия диссоциации этой молекулы. Если в уравнение Шредингера вместо
где we-равновесная частота колебаний (см-1) wexe- постоянная ангaрмoничности (см-1)
Отметим, что реальная молекула имеет наименьшую энергию Eo – энергию основного колебательного состояния:
поэтому в действительности энергия диссоциации равна Do, а не De.
Перепишем формулу (4.19) в виде
и сравним с уровнями энергии гармонического осциллятора
по аналогии можно записать
Другими словами, ангармонический осциллятор ведет себя подобно гармоническому осциллятору, частота которого постоянно уменьшается с ростом v.
Правила отбора для переходов ангармонического осциллятора
Dv = ±1, ±2, ±3… (4.21)
Таким образом, по сравнению с гармоническим осциллятором здесь возможны переходы с большим, чем 1, изменением v. Однако вероятность перехода сильно убывает с увеличением Dv. Сколько-нибудь заметной интенсивностью обладают лишь линии с Dv = ±1, ±2, ±3. Более того, можно показать (см.§4.2 Статистическое распределение молекул по энергетическим состояниям), что заселенность состояния v=1 при комнатной температуре составляет всего
Спектральная линия называется основной линией поглощения.
2) 0®2 слабый переход (4.22) De = e2 - e0 = 2wе - 6wеxе см-1 Спектральная линия называется первым обертоном 3) 0 ®3 очень слабый De = e3 - e0 = 3wе - 12wеxe см-1 Спектральная линия называется вторым обертоном
Так как wеxe мало, то спектральные линии, соответствующие этим переходам расположены около we, 2we, и 3we.
Например, в ИК спектре молекулы HCl наблюдается очень интенсивная линия поглощения при 2886 см-1, слабая - 5668 см-1 и очень слабая - 8347 см-1. Из приведенных данных можно найти равновесную частоту we и коэффициент ангармоничности wexe, для чего нужно решить любые 2 из 3-х уравнений: we - 2wexe = 2886 2we - 6wexe = 5668 3we - 12wexe = 8347 что дает we=2990см-1, wexe=52. Отсюда видно, что в отличие от идеального гармонического осциллятора, для которого спектральное поглощение имело место точно на равновесной частоте колебаний, для реальных ангармонических молекул наблюдаемая основная частота поглощения и равновесная частота могут значительно отличаться. Зная we и приведенную массу m, можно найти силовую постоянную. Используя формулу (4.14) k = 4p2we2c2m (H•м-1) (4.23)
Хотя мы и пренебрегли переходами из v = 1 в более высокие состояния, нужно отметить, что при повышенной температуре или для более низкочастотных колебаний населенность состояния v = 1 может быть заметной и тогда интенсивность спектральных линий, соответствующих переходам с этого уровня, повышается. Переход 1 – 2 D v = + 1 обычно очень слабый переход D e = we - 4wexe см-1 Таким образом, когда это слабое поглощение возникает, оно появляется вблизи линии основного поглощения при несколько мéньшем значении волнового числа (т.к. xe > 0 и мало). Такие слабые линии поглощения называются горячими полосами, т.к. главным их признаком является увеличение интенсивности с ростом температуры образца.
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 2787; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.85.123 (0.013 с.) |

 Атомы связаны жестким стержнем (связью) длиной r0. Концы молекулы вращаются вокруг точки С - центра тяжести. Момент инерции относительно точки С
Атомы связаны жестким стержнем (связью) длиной r0. Концы молекулы вращаются вокруг точки С - центра тяжести. Момент инерции относительно точки С
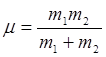 - приведенная масса
- приведенная масса (Дж) J=0,1,2… (4.8)
(Дж) J=0,1,2… (4.8) (cм-1) J=0,1,2… (4.9)
(cм-1) J=0,1,2… (4.9) (см-1) (4.10)
(см-1) (4.10) (см-1) - вращательная постоянная (4.11)
(см-1) - вращательная постоянная (4.11) Последовательность разрешенных энергетических уровней, определяемых соотношением (4.10), показана на рис.2.
Последовательность разрешенных энергетических уровней, определяемых соотношением (4.10), показана на рис.2. (см-1)
(см-1)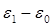 (4.12)
(4.12) (см-1)
(см-1)
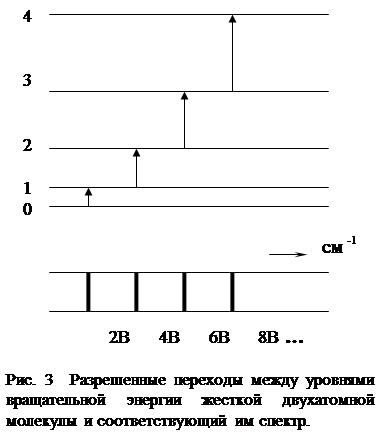

 (см –1) (4.13)
(см –1) (4.13) или B ~ r -2
или B ~ r -2



 Существование устойчивой двухатомной молекулы можно считать следствием равновесия двух сил. С одной стороны, имеется отталкивание между положительно заряженными ядрами обоих атомов и между отрицательно заряженными электронными облаками, с другой - притяжение между ядром одного атома и электронами другого, и наоборот. Два атома располагаются на таком межъядерном расстоянии, при котором эти силы точно уравновешены и энергия молекулы минимальна. Это расстояние называется равновесным re или длиной связи. Поведение связи при сжатии и растяжении можно сравнить с поведением пружины и предположить, что связь, подобно пружине, подчиняется закону Гука:
Существование устойчивой двухатомной молекулы можно считать следствием равновесия двух сил. С одной стороны, имеется отталкивание между положительно заряженными ядрами обоих атомов и между отрицательно заряженными электронными облаками, с другой - притяжение между ядром одного атома и электронами другого, и наоборот. Два атома располагаются на таком межъядерном расстоянии, при котором эти силы точно уравновешены и энергия молекулы минимальна. Это расстояние называется равновесным re или длиной связи. Поведение связи при сжатии и растяжении можно сравнить с поведением пружины и предположить, что связь, подобно пружине, подчиняется закону Гука:

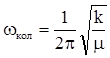 (Гц) (4.14)
(Гц) (4.14) (см-1)
(см-1) (Дж) v=0,1,2… (4.15)
(Дж) v=0,1,2… (4.15) (см-1)
(см-1) (Дж) (4.16)
(Дж) (4.16) (см-1)
(см-1) Из уравнения Шредингера для гармонического осциллятора вытекают правила отбора
Из уравнения Шредингера для гармонического осциллятора вытекают правила отбора

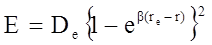 (4.18)
(4.18)
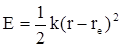 (гармонический осциллятор) подставить выражение (4.18), то разрешенные колебательные энергии описываются выражением:
(гармонический осциллятор) подставить выражение (4.18), то разрешенные колебательные энергии описываются выражением: (см-1)
(см-1)  (4.19)
(4.19) wexe << we, поэтому с ростом v колебательные уровни все более тесно сближаются друг с другом:
wexe << we, поэтому с ростом v колебательные уровни все более тесно сближаются друг с другом: (4.20)
(4.20)



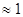 % от населенности основного состояния (для v>1). Поэтому с достаточно хорошей точностью можно пренебречь всеми переходами с уровней v³1 и ограничиться тремя:
% от населенности основного состояния (для v>1). Поэтому с достаточно хорошей точностью можно пренебречь всеми переходами с уровней v³1 и ограничиться тремя: 1) 0®1
1) 0®1  сильный переход.
сильный переход. (см-1)
(см-1)
 , получим
, получим


