
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колебательно – вращательные переходы в двухатомной молекуле.Содержание книги
Поиск на нашем сайте
Если учесть, что каждый колебательный уровень имеет вращательные подуровни (рис.1), то каждая линия в колебательном спектре на самом деле состоит из множества линий, которые становятся видны при бóльшем разрешении спектрального прибора. Рассмотрим структуру колебательно-вращательного спектра. Расстояние между вращательными энергетическими уровнями для типичной двухатомной молекулы составляет 1 – 10 см-1, а между колебательными»3000 см-1. Так как энергии двух этих форм движения столь различны, то в первом приближении можно считать, что двухатомная молекула совершает вращение и колебания совершенно независимо. Это равносильно допущению, что колебательно-вращательная энергия есть сумма eкол-вращ = eвращ + eкол (см-1) или eJ,v = eJ + ev Подставим значения eJ (нежесткий ротатор) и ev (ангармонический осциллятор): eJ,v = B•J•(J+1) - D•J2•(J+1)2 + we•(v+ Пренебрежем малой константой центробежного растяжения D: eJ,v = B•J•(J+1) + we•(v+ Конечно, пренебрегать величиной D не очень логично, так как это означает, что молекула считается жесткой и в то же время колеблющейся! Но учет D приводит лишь к слабым изменениям спектра молекулы.
Правила отбора для переходов молекулы из одного колебательно-вращательного состояния в другое Dv = ±1, ±2, ±3... DJ = ±1 На рисунке изображены некоторые переходы с основного колебательного состояния в первое возбужденное колебательное состояние, а внизу приведены соответствующие этим переходам спектральные линии. Поскольку нижние вращательные уровни J” имеют разную заселенность (см.§4.2), то спектральные линии имеют разную интенсивность, что отражено их высотой.
Рассчитаем положение этих спектральных линий в колебательно-вращательном спектре на примере основной линии поглощения. Во-первых, на рисунке нет спектральной линии с волновым числом, равным nо =wе - 2wеxе, т.е. линии, вызванной переходом из состояния v = 0, J’’ = 0 в состояние v = 1, J’ = 0. Это связано с тем, что хотя разрешено Dv = +1, но запрещено DJ = 0. Место этой несуществующей спектральной линии на рисунке изображено пунктиром.
Во-вторых, по правилам отбора DJ = ±1 и поэтому осуществляются две серии переходов между вращательными состояниями разных колебательных уровней. Соответственно, в спектре наблюдаются две серии линий, которые называются ветвями полос: R-ветвями, если DJ = +1 и P-ветвями, если DJ = -1. Найдем аналитическое выражение для положения спектральных линий в R- и P- ветвях основной линии поглощения:
Для R-ветви DJ = J’ – J” = +1, т.е. J’ = J”+1 DeJ,v = B•J’•(J’+1) + we•(v+1+ –wexe(v+ где J”=0,1,2… Задание на дом: выполнить промежуточные вычисления. Для P-ветви
Для удобства две ветви можно описать одной формулой
где m = 1,2,3… для R-ветви m= m = -1,-2,-3… для P-ветви m=
Таким образом, каждая спектральная линия в колебательном спектре молекулы состоит из большого количества близко расположенных спектральных вращательных линий, которые при малом разрешении спектрометра сливаются в одну линию.
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 1025; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.009 с.) |

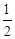 ) - we•xe(v+
) - we•xe(v+  )2
)2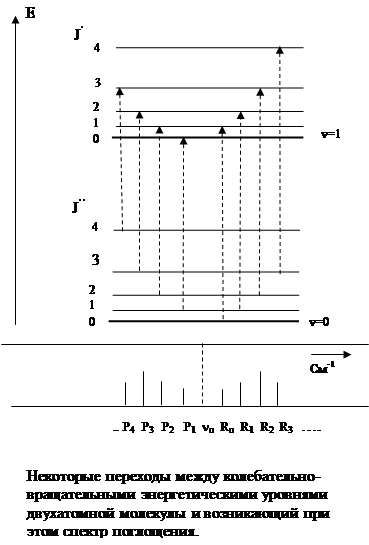 Уровни энергии двухатомной молекулы, рассчитанные по формуле (4.27), изображены на рисунке. Масштаб здесь не соблюден: вращательные уровни, конечно, лежат гораздо ближе друг к другу, так как в действительности расстояние между вращательными уровнями в ~1000 раз меньше, чем между колебательными. Вращательные квантовые числа в состоянии v = 0 обозначены J”, в состоянии v = 1 как J’. Такое обозначение принято в спектроскопии.
Уровни энергии двухатомной молекулы, рассчитанные по формуле (4.27), изображены на рисунке. Масштаб здесь не соблюден: вращательные уровни, конечно, лежат гораздо ближе друг к другу, так как в действительности расстояние между вращательными уровнями в ~1000 раз меньше, чем между колебательными. Вращательные квантовые числа в состоянии v = 0 обозначены J”, в состоянии v = 1 как J’. Такое обозначение принято в спектроскопии.
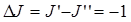 т.е.
т.е. 
 J,v = n0 - 2B(
J,v = n0 - 2B(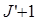 )
) 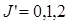 …
…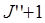 и
и


