
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Строение вещества. Конспект лекций по дисциплине «строение вещества» предназначен для студентов 2-курса химического факультетаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
СТРОЕНИЕ ВЕЩЕСТВА Конспект лекций В.М. Янборисов Конспект лекций по дисциплине «Строение вещества» предназначен для студентов 2-курса химического факультета
Содержание Введение............................................................................................................................................. 3 Классическая и квантово-механическая теории строения молекул......................................... 3 Тема 1. Классическая модель молекулы..................................................................................... 4 1.1 Основные понятия................................................................................................................... 4 1.2 Координаты атомов (ядер) молекулы.................................................................................... 5 1.3 Равновесная геометрическая конфигурация молекулы....................................................... 5 1.4 Межъядерные расстояния, валентные углы, углы внутреннего вращения....................... 6 1.5 Отталкивание электронных пар............................................................................................. 8 1.5.1 Молекулы с s-связями..................................................................................................... 8 1.5.2 Молекулы с p-связями.................................................................................................... 10 1.6 Закономерности в геометрической конфигурации молекул............................................ 11 1.6.1 Закономерности в равновесных значениях длин связей............................................ 11 1.6.2 Закономерности в валентных углах............................................................................. 12 1.6.3 Закономерности в углах внутреннего вращения, конформеры................................. 13 1.6.4 Внутреннее вращение в 1,2-дихлорэтане..................................................................... 15 Тема 2. Симметрия молекул........................................................................................................ 17 Тема 3. Электрические свойства молекул................................................................................ 20 3.1 Дипольные моменты молекул.............................................................................................. 20 3.1.1 Электрический дипольный момент в классической теории...................................... 20 3.1.2 Полярные и неполярные молекулы. Дипольный момент и симметрия молекул.... 22 3.1.3 Дипольный момент и изомерия молекул..................................................................... 24
3.3 Связь электрических свойств молекул с электрическими свойствами вещества.......... 26 3.3.1 Поляризация диэлектриков........................................................................................... 26 3.3.2 Поляризация диэлектрика в переменном поле............................................................ 28
3.3.3 Мольная рефракция........................................................................................................ 28 Тема 4. Электронно-колебательно-вращательные состояния молекул............................. 29 4.1 Энергетические состояния двухатомной молекулы.......................................................... 29 4.2 Статистическое распределение молекул по энергетическим состояниям...................... 32 4.3 Спектральные области.......................................................................................................... 33 4.4 Вращательные состояния молекул....................................................................................... 36 4.4.1 Двухатомная молекула как жесткий ротатор............................................................... 37 4.4.2 Нежесткий ротатор......................................................................................................... 39 4.5 Колебательные состояния..................................................................................................... 41 4.5.1 Гармонический осциллятор........................................................................................... 41 4.5.2 Ангармонический осциллятор...................................................................................... 43 4.5.3 Колебательно – вращательные переходы в двухатомной молекуле......................... 46 4.5.4. Взаимодействие вращений и колебаний..................................................................... 48 4.6 Спектроскопия комбинационного рассеяния..................................................................... 49 4.6.1 Квантовый подход к КР................................................................................................. 49 4.6.2 Вращательные спектры комбинационного рассеяния линейных молекул.............. 50 4.6.3. Колебательные спектры КР.......................................................................................... 51 4.7 Электронные спектры двухатомных молекул.................................................................... 53 5.7.1 Интенсивность электронно-колебательных спектров: принцип.............................. 54 Франка-Кондона...................................................................................................................... 54 ЛИТЕРАТУРА:.............................................................................................................................. 57
Введение. Тема 1. Классическая модель молекулы. Основные понятия. Важно, что в классической модели атома или молекулы электроны никогда явным образом не рассматриваются. В классической теории молекула рассматривается как совокупность «эффективных атомов»: молекула существует как единое целое благодаря взаимодействиям между эффективными атомами – главными и дополнительными. Слово «эффективный» употребляется для того, чтобы подчеркнуть, что атом в составе молекулы отличается от свободного атома. Если ядро у эффективного и свободного атомов одно и то же, то электронные оболочки существенно различаются по своей форме, а иногда и по количеству электронов. Таким образом, у каждого эффективного атома существует положительно заряженное ядро, массу эффективного атома можно считать сосредоточенной в ядре и принять это ядро за центр эффективного атома.
В дальнейшем для краткости вместо термина «эффективный атом» будем использовать «атом».
Молекулы с s-связями. Во многих случаях можно предсказать форму ковалентных молекул исходя из простого предположения, что электронные пары валентных орбиталей стремятся расположиться возможно дальше друг от друга. Например, в ряду хлоридов: BeCl2 (в газовой фазе), BCl3 и CCl4 атом хлора присоединен к бериллию, бору и углероду простой 2-х электронной связью. Тогда взаимное отталкивание этих электронных пар должно придать молекулам линейную, плоскую тригональную и тетраэдрическую формы соответственно (атомы хлора не изображены):
линейнаяплоская тригональнаятетраэдрическая
В приведенных молекулах в образовании связи участвуют все валентные электроны центрального атома. Однако в общем случае необходимо учитывать и те валентные электроны, которые не образуют связи. Поясним это на примере ряда гидридов: CH4, NH3 и H2O. Экспериментальные значения валентных углов в этих молекулах соответственно равны 109,5, 107,1 и 104,5о. Следует ожидать, что метан будет иметь правильную тетраэдрическую форму с одинаковыми углами HCH, так как все 4 валентных электронов углерода участвуют в образовании связей С-Н, и при этом 4 связывающие пары электронов будут расположены максимально далеко друг от друга.
Аналогичен подход и к молекуле воды. Из шести валентных электронов атома кислорода два электрона участвуют в образовании двух связей O-H, образуя две связывающие пары с электронами атомов водорода. Четыре оставшихся электрона образуют две неподеленные пары. Неподеленные пары здесь также будут занимать больше места, чем связывающие, следствием чего будет сближение двух связей О-Н и уменьшение угла до 104,5о.
Итак, уменьшение угла между связями в ряду молекул CH4, NH3 и H2O можно объяснить, предположив, что отталкивание между электронными парами увеличивается в последовательности: связывающая пара – связывающая пара, связывающая пара – неподеленная пара, неподеленная пара - неподеленная пара. Изложенное выше справедливо, разумеется, не только для гидридов. Все ковалентные соединения углерода, азота, кислорода и фтора, которые содержат только s-связи, можно рассматривать, исходя из тетраэдрического расположения связывающих и неподеленных пар электронов. Бериллий и бор используют все свои электроны для образования связей, так что нет необходимости заботиться о неподеленных парах электронов. Следовательно, молекулы BeX2 и BX3 принимают, соответственно, линейную и плоскую тригональную конфигурации. Однако, у Be и B существует заметное стремление достичь более высокой тетраэдрической симметрии, приобретая добавочные электронные пары за счет других молекул. Например, BF3 действует как акцептор электронов (кислота Льюиса) и принимает электронную пару от подходящих доноров (оснований по Льюису), таких как молекула аммиака. При этом образуется донорно-акцепторное или координационное соединение
Обратите внимание на средние лепестки.
Когда неподеленная пара электронов аммиака приближается к плоской молекуле BF3, между ней и тремя парами электронов, образующими связи B-F, возникает отталкивание. Это превращает плоскую молекулу BF3 в пирамиду и при образовании связи с атомом азота приводит примерно к тетраэдрическому расположению связей относительно атома бора.
Молекулы с p-связями. До сих пор мы рассматривали только s-связи, однако многие молекулы имеют еще и p-связи. Тем не менее, p-связи не влияют на основные стереохимические закономерности. Особенно хорошо это видно на примере соединений углерода. Для всех насыщенных соединений углерода расположение связей является тетраэдрическим, но если углерод связан меньше чем с четырьмя атомами, то симметрия соединений будет более низкая. Присоединение к углероду только трех атомов, как, скажем, в COCl2 или C2H4, приводит к плоскому тригональному расположению связей относительно атома углерода:
Хотя кратные связи не изменяют плоскую форму молекулы, углы между связями могут заметно отличаться от 120о, поскольку электроны кратной связи занимают большее пространство, чем электроны одинарной связи. Так, угол Cl-C-Cl в COCl2 уменьшен до 111о. Если углерод связан только с двумя атомами, молекула имеет линейную форму с двумя s- и двумя p-связями. При этом она может иметь остов вида =С= или –Сº. Типичными примерами могут служить молекулы CO2 и NCH: O = C = O H – C º N Итак, метод отталкивания электронных пар может с успехом применяться для предсказания конфигурации простых молекул. Обычно этот метод используется для соединений первого и второго периодов Периодической таблицы и в более ограниченной степени для соединений других элементов. Элементы второго периода не могут образовать более четырех ковалентных связей (почему?), а у элементов последующих периодов это число может возрастать до 6-ти и более связей. Поэтому у более тяжелых элементов следует ожидать появления других конфигураций, кроме линейной, плоской тригональной и тетраэдрической.
Тема 2. Симметрия молекул. Представления о симметрии очень важны как в связи с теоретическим, так и экспериментальным изучением атомов и молекул. Основные принципы симметрии применяются в квантовой механике, спектроскопии и для определения структуры при помощи дифракции нейтронов, электронов и рентгеновских лучей. Некоторые расчеты значительно упрощаются, если принимать во внимание симметрию молекулы. Симметрией определяется также, может ли быть молекула оптически активной или иметь дипольный момент. Под операциями симметрии для молекулы подразумеваются операции отражения молекулы в плоскости, поворота молекулы как целого вокруг некоторой оси, отражение в центре, и, наконец, вращение вокруг некоторой оси с последующим отражением в плоскости. Этим операциям симметрии соответствуют элементы симметрии: плоскости симметрии, оси симметрии, центр симметрии и зеркально-поворотные оси симметрии.
Рассмотрим молекулу формальдегида H2CO. Эта молекула имеет две плоскости симметрии, при отражении в которых она не меняется. Первая вертикальная плоскость симметрии sv проходит через ядра всех атомов. Вторая вертикальная плоскость симметрии sv’ перпендикулярна первой и проходит через биссектрису угла HCH. При отражении ядра C и О сохраняют свои положения, а эквивалентные ядра Н меняются местами, что не связано с какими-либо изменениями в строении или свойствах молекулы. Ось симметрии n-го порядка (обозначается Cn ). Осью симметрии n-го порядка называется такая ось, при повороте вокруг которой на угол 360/n молекула не меняется. Рассмотренная выше молекула формальдегида помимо двух плоскостей симметрии имеет ось симметрии второго порядка C2, проходящую через линию пересечения плоскостей. При повороте 360/2=180о вокруг этой оси ядра С и О остаются на своих местах, а ядра Н меняются местами. Молекулы могут иметь ось симметрии следующих порядков: 1,2,3…6 и ∞.
Центр симметрии (обозначается i ).
Зеркально-поворотная ось симметрии n-го порядка (Sn).
Например, цис-конформер этана имеет ось симметрии C3 (она же – зеркально-поворотная ось S3), а также зеркальную плоскость, которая перпендикулярна оси С3 и обозначается sh. Эта плоскость отличается от плоскости для транс-конформера тем, что является зеркальной. Есть ли на этом рисунке центр симметрии?
Для транс-конформера этана имеется зеркально-поворотная ось шестого порядка, при повороте вокруг которой на 60о и последующем отражении в плоскости, изображенной на рисунке, молекула не меняется. Плоскость, изображенная здесь, не является зеркальной. Есть ли на этом рисунке центр симметрии?
Молекула может иметь несколько осей симметрии разных порядков. В этом случае одна из осей наивысшего порядка называется главной осью симметрии. Рисуют молекулу так, чтобы главная ось симметрии была расположена вертикально (см. рисунки). Здесь изображена проекция транс-конформера этана (вид снизу).
Группы симметрии. Все возможные сочетания элементов симметрии (операций симметрии), которые могут встречаться в молекулах, можно подразделить на строго определенное число групп симметрии. Следовательно, каждая молекула в соответствии с ее элементами симметрии, т.е. теми операциями, при которых она не меняется, может быть отнесена к определенной группе симметрии. Как найти группу симметрии какой-либо молекулы?
Во-первых, необходимо знать конфигурацию молекулы и зарисовать ее (лучше в нескольких проекциях).
Во-вторых, нужно найти все элементы симметрии этой молекулы: - начинать следует с поиска осей симметрии и выделения среди них главной оси симметрии; как только главная ось найдена, следует перерисовать молекулу, расположив главную ось вертикально - далее, нужно найти все плоскости симметрии и определить их тип sv, sh, или sd - наконец, отыскать зеркально-поворотные оси и центр симметрии. Следует отметить, что наличие у молекулы некоторых элементов симметрии обусловливает обязательное наличие и других элементов симметрии. Если молекула имеет две взаимно перпендикулярные плоскости симметрии, то линия пересечения этих плоскостей будет осью симметрии С2. Наличие оси С2 и плоскости, ей перпендикулярной, обусловливает наличие центра симметрии и зеркально-поворотной оси S2 и т.п.
В-третьих, по набору найденных элементов симметрии определить группу симметрии, пользуясь следующей таблицей.
Обычные точечные группы Шенфлиса.
Дипольные моменты молекул. Поляризация диэлектриков. Одной из важных электрических характеристик (парообразного) вещества, состоящего из молекул определенного строения, являются его диэлектрическая проницаемость e. Между макроскопической характеристикой вещества - его диэлектрической проницаемостью e, с одной стороны, и микроскопическими характеристиками отдельных молекул этого вещества – поляризуемостью а и собственным дипольным моментом m, с другой стороны, может быть установлена определенная зависимость. Мы рассмотрим этот вопрос на основе классической физики. Именно, мы не будем принимать во внимание ни квантование проекции дипольного момента молекулы, ни квантование вращательной энергии молекулы. Также не будем учитывать различий в дипольных моментах отдельных молекул, находящихся в разных электронных, колебательных и вращательных состояниях. Учет всех этих факторов в случае относительно слабых полей и высоких температур (порядка комнатной и выше) приводит в первом приближении к результатам, аналогичным получающимся на основе классической физики. Рассмотрим изменение состояний отдельных молекул и вещества в целом при помещении его в однородное электрическое поле, например в поле плоского конденсатора. Если в отсутствие диэлектрика напряженность в плоском конденсаторе была Е, то при введении между его обкладками диэлектрика напряженность поля Е/ станет меньше в e раз.
Это уменьшение напряженности происходит потому, что диэлектрик поляризуется, то есть на его поверхностях, обращенных к обкладкам конденсатора, появляются избыточные заряды. Плотность зарядов на единицу поверхности, появляющихся на поверхностях, примыкающих к обкладкам конденсатора, обозначим через Р - поверхностная плотность зарядов.
Поляризация диэлектрика в поле объясняется двумя причинами. Во-первых, при помещении в поле в каждой молекуле индуцируется момент Во-вторых, при помещении в поле молекул, имеющих собственные дипольные моменты
где Рi - поверхностная плотность заряда за счет индуцированного Р0 - за счет ориентации собственных моментов m.. Если выразить Рi и Р0 через микроскопические характеристики а и m и учесть зависимость между Р и e, то можно получить уравнение Ланжевена-Дебая. Уравнение Ланжевена-Дебая для единицы объема вещества.
Где N - число молекул в единице объема, k - постоянная Больцмана, Т - температура,
Если (3.9) умножить на объем одного моля
И учесть, что N1• VM=NA – число Авогадро, то
PM - мольная поляризация.
Уравнение Ланжевена-Дебая для неполярных молекул (m = 0):
Мольная рефракция. Так как в видимой и ультрафиолетовой области спектра проще измерять показатель преломления n, чем диэлектрическую проницаемость e, то, основываясь на соотношении
Значение мольной рефракции Rm обычно измеряют для некоторых частот (длин волн) видимой или УФ-области, которые экспериментально наиболее доступны. В частности, значения показателя преломления n и мольной рефракции часто приводят для D линии натрия (l=5893A0), для отдельных линий спектра ртути и водорода. Спектральные области. Электромагнитное излучение, связанное с переходами между электронно-колебательно-вращательными уровнями энергии молекулы, можно проиллюстрировать следующей таблицей. Для того чтобы падающее излучение могло вызвать эти переходы, они должны сопровождаться изменениями электрических свойств молекулы: либо должен изменяться электрический дипольный момент (см. области спектра излучения в таблице), либо должна изменяться поляризуемость молекулы (спектры комбинационного рассеяния).
1 100 104 106 108
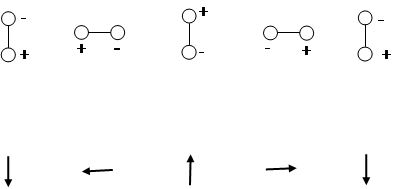
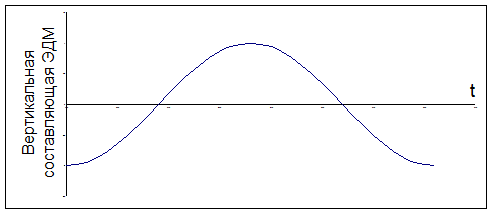
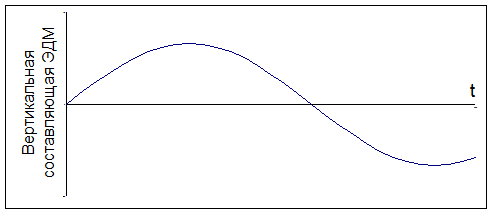
Рассмотрим, каким образом движение (молекулы, атомов или электронов), отраженное в таблице, приводит к изменению электрического дипольного момента. Микроволновая область. В полярной молекуле типа HCl один атом заряжен положительно, а другой отрицательно, т.е. молекула обладает собственным электрическим дипольным моментом. При вращении этой молекулы как целого вокруг собственного центра масс абсолютное значение дипольного момента останется, естественно, неизменным. Однако его направление будет изменяться во время вращения, и составляющая дипольного момента в некотором выделенном направлении будет испытывать регулярные изменения:
Эти изменения подобны изменениям электромагнитного поля: Поэтому благодаря своему вращению молекула будет взаимодействовать с излучением, поглощая или излучая при этом энергию, иными словами возникает вращательный спектр. Обо всех молекулах, имеющих собственный электрический дипольный момент, говорят, что они «активны в микроволновой области». Если же молекула не имеет собственного дипольного момента (H2, Cl2 и т.п.), то она «неактивна в микроволновой области». Таким образом, неполярные молекулы невозможно исследовать с помощью микроволновой спектроскопии. Инфракрасный диапазон (ИК спектры). Здесь изменение дипольного момента вызывается колебаниями атомов. В качестве примера рассмотрим молекулу двуокиси углерода CO2, имеющую линейную форму (почему?).
растянута
в равновесии
сжата Ясно, что в течение всего периода колебаний дипольный момент равен нулю и поэтому симметричное валентное колебание неактивно в ИК области. Однако имеется другое колебание – валентное асимметричное. При возбуждении этого колебания в молекуле CO2 одна связь СО связь сжимается, в то время как другая – растягивается:
Эта же молекула может совершать колебание еще одного типа – деформационное. Оно, как можно видеть, также активно в ИК области.
Сам факт проявления или не проявления в спектре определенных колебательных частот, соответствующих тому или иному типу колебаний, дает ценную информацию о структуре исследуемой молекулы.
Видимая и ультрафиолетовая области. Излучение или поглощение молекулами электромагнитных волн в этой области спектра связано с изменением электрического дипольного момента молекулы при возбуждении валентных электронов. Если же перераспределение электронной плотности происходит в результате возбуждения внутренних электронов, то появляется рентгеновский спектр.
Нежесткий ротатор. Спектральные линии в спектре жесткого ротатора должны отстоять друг от друга на расстояние 2B. Однако в реальных спектрах расстояния между соседними линиями, а, следовательно, и эффективные значения B монотонно уменьшаются с ростом J. Причина этого уменьшения заключается в том, что с ростом скорости вращения двухатомной молекулы (т.е. с увеличением J) увеличивается центробежная сила, растягивающая связь и приводящая к увеличению ее длины. Таким образом, допущение о жесткости связи в модели жесткого ротатора является всего лишь приближенным: в действительности все связи до некоторых пределов упруги (см. § 4.5.2). Остановимся кратко на двух следствиях этого свойства химических связей. Во-первых, если связь упруга, молекула может обладать колебательной энергией – энергией периодического растяжения и сжатия связи с определенной частотой, зависящей от масс атомов и от упругости (или силовой постоянной) связи. Ясно, что зависимость B от J должна определяться этой силовой постоянной: чем слабее связь, тем сильнее она деформируется под действием центробежных сил. Вторым следствием упругости связи является то, что при колебаниях величины r и B меняются. При вращении за время одного оборота успевают произойти сотни колебаний связи, и, следовательно, измеренная микроволновыми методами величина r является усредненной. Из определения B следует
Для реальной связи r > re. Поэтому приходится определять несколько наборов значений B и r. Равновесному расстоянию между ядрами re соответствует вращательная постоянная Be – жесткая связь – модель жесткого ротатора. Основное колебательное состояние характеризуется средним межъядерным расстоянием ro, которому соответствует вращательная постоянная Bo. В общем случае, если двухатомная молекула обладает колебательной энергией Ev, то она будет характеризоваться соответствующими значениями rv и Bv (v – колебательное квантовое число). Иногда можно пренебречь малыми различиями между Be, Bo и Bv. Далее в настоящем параграфе мы сделаем это и будем обозначать вращательную постоянную просто B. Из уравнения Шредингера для двухатомной молекулы как нежесткого ротатора разрешены следующие энергетические состояния (термы): eJ = B•J•(J+1) - D•J2•(J+1)2 где D – постоянная центробежного растяжения. Значение D меньше значения B на несколько порядков, и поэтому при малых J поправочный член D•J2•(J+1)2 можно не учитывать, но при J>10 центробежное растяжение сказывается сильно и его необходимо учитывать. На рис. На стр.38 схематически изображено понижение уровней вращательной энергии при переходе от жестких к нежестким молекулам, а также вызванное этим изменение спектров. Отметим, что, по прежнему, правила отбора DJ = ± 1. Выражение для волнового числа спектральных линий nJ = eJ+1 - eJ = B(J+1)(J+2) – D(J+1)2(J+2)2 – BJ(J+1) + DJ2(J+1)2 = = 2B(J+1) – 4D(J+1)3 (см-1) Из этого аналитического выражения видно, что спектр упругого ротатора похож на спектр жесткого ротатора, за исключением того, что в нем каждая линия несколько смещена в область низких частот, причем смещение возрастает пропорционально (J+1)3:
Э нергетические уровни Жесткий ротатор Упругий ротатор
Спектры
Колебательные состояния. Гармонический осциллятор.
где f-сила упругости, k-силовая постоянная, r - межъядерное расстояние.
Такая модель молекулы называется гармоническим осциллятором. Энергия гармонического осциллятора (Рис. 4) описывается формулой
Упругая связь, подобно пружине, имеет определенную частоту колебаний, зависящую от массы системы и силовой постоянной, но не от величины деформации:
или
Разрешенные уровни колебательной энергии могут быть найдены из уравнения Шредингера для гармонического осциллятора
или
Отсюда видно, что наименьшая колебательная энергия при v = 0 равна
или
это означает, что колебательная энергия двухатомной (а в действительности и любой другой) молекулы никогда не может равняться нулю, т.е. атомы никогда не могут быть полностью неподвижны относительно друг друга. Наличие нулевой энергии является отраж
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 1158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.195.205 (0.014 с.) |

 3.2 Поляризуемость молекулы................................................................................................. 25
3.2 Поляризуемость молекулы................................................................................................. 25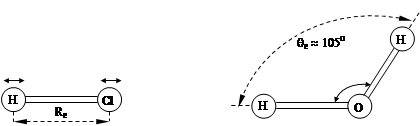 Молекула как целое может
Молекула как целое может  Во-вторых, одни группы эффективных атомов молекулы могут совершать крутильные колебания или вращаться по отношению к другим группам атомов (
Во-вторых, одни группы эффективных атомов молекулы могут совершать крутильные колебания или вращаться по отношению к другим группам атомов ( 2 связывающие пары 3 связывающие пары 4 связывающие пары
2 связывающие пары 3 связывающие пары 4 связывающие пары В молекуле же аммиака только 3 из пяти валентных электронов азота участвуют в образовании связей N-H, а два оставшихся валентных электрона образуют неподеленную пару. Неподеленная пара электронов займет вблизи ядра атома азота несколько больший объем, чем связывающая пара. В результате взаимного отталкивания связывающие пары будут слегка прижаты одна к другой, что приведет к несколько меньшему (107,1о), чем тетраэдрическое (109,5о) значению угла HNH. Таким образом, расположение электронных пар в молекуле аммиака можно назвать псевдотетраэдрическим. Однако форма молекулы аммиака называется
В молекуле же аммиака только 3 из пяти валентных электронов азота участвуют в образовании связей N-H, а два оставшихся валентных электрона образуют неподеленную пару. Неподеленная пара электронов займет вблизи ядра атома азота несколько больший объем, чем связывающая пара. В результате взаимного отталкивания связывающие пары будут слегка прижаты одна к другой, что приведет к несколько меньшему (107,1о), чем тетраэдрическое (109,5о) значению угла HNH. Таким образом, расположение электронных пар в молекуле аммиака можно назвать псевдотетраэдрическим. Однако форма молекулы аммиака называется 


 С∞ - любые углы поворота (линейные молекулы):
С∞ - любые углы поворота (линейные молекулы): Центром симметрии называется такая точка, при отражении в которой молекула не меняется. Например молекула этилена имеет центр симметрии на середине расстояния между ядрами углерода. При отражении в этой точке ядра углерода и ядра водорода (крест накрест) меняются местами, что не приводит к изменению в строении и свойствах молекулы.
Центром симметрии называется такая точка, при отражении в которой молекула не меняется. Например молекула этилена имеет центр симметрии на середине расстояния между ядрами углерода. При отражении в этой точке ядра углерода и ядра водорода (крест накрест) меняются местами, что не приводит к изменению в строении и свойствах молекулы. Это такая ось, при повороте вокруг которой на углы 360/n и последующего отражения в плоскости, перпендикулярной этой оси, молекула не меняется.
Это такая ось, при повороте вокруг которой на углы 360/n и последующего отражения в плоскости, перпендикулярной этой оси, молекула не меняется.
 Например, транс-конформер этана помимо главной оси симметрии C3 имеет еще три оси симметрии С2, изображенные на рисунке непрерывными линиями и проходящие через центр связи С-С. Как следствие, возникает еще одни элемент симметрии –
Например, транс-конформер этана помимо главной оси симметрии C3 имеет еще три оси симметрии С2, изображенные на рисунке непрерывными линиями и проходящие через центр связи С-С. Как следствие, возникает еще одни элемент симметрии – 
 или
или 
 , который при равновероятных произвольных ориентациях молекул в поле оказывается в среднем направлен по полю. Это происходит потому, что ядра каждой молекулы в среднем смещаются по полю, а электронное облако - против поля и таким образом положительные заряды наведенных диполей в среднем оказываются направленными в сторону отрицательной пластины конденсатора.
, который при равновероятных произвольных ориентациях молекул в поле оказывается в среднем направлен по полю. Это происходит потому, что ядра каждой молекулы в среднем смещаются по полю, а электронное облако - против поля и таким образом положительные заряды наведенных диполей в среднем оказываются направленными в сторону отрицательной пластины конденсатора. , молекулы частично ориентируются по полю, в результате средняя составляющая их собственных моментов оказывается направленной по полю. Поэтому поверхностная плотность зарядов складывается из двух частей:
, молекулы частично ориентируются по полю, в результате средняя составляющая их собственных моментов оказывается направленной по полю. Поэтому поверхностная плотность зарядов складывается из двух частей: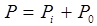 ,
, ,
, (3.9)
(3.9) часто называется удельной поляризацией (на единицу объема)
часто называется удельной поляризацией (на единицу объема)
 (3.10)
(3.10)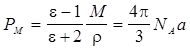 (3.11)
(3.11) , можно ввести n 2 в место e в уравнение (3.11) для Рм. Мольную поляризацию Рм для частот видимой и УФ-области, выраженную через n 2 вместо e, обычно называют мольной рефракцией
, можно ввести n 2 в место e в уравнение (3.11) для Рм. Мольную поляризацию Рм для частот видимой и УФ-области, выраженную через n 2 вместо e, обычно называют мольной рефракцией (3.12)
(3.12)
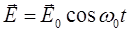 .
.
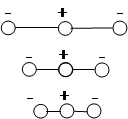 При возбуждении колебания, называемого симметричным валентным, молекула попеременно растягивается и сжимается так, что обе связи С-О изменяются синхронно:
При возбуждении колебания, называемого симметричным валентным, молекула попеременно растягивается и сжимается так, что обе связи С-О изменяются синхронно:
 Валентное асимметричное колебание активно в ИК области.
Валентное асимметричное колебание активно в ИК области.
 или B ~ r -2
или B ~ r -2



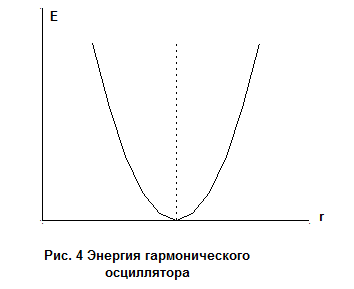 Существование устойчивой двухатомной молекулы можно считать следствием равновесия двух сил. С одной стороны, имеется отталкивание между положительно заряженными ядрами обоих атомов и между отрицательно заряженными электронными облаками, с другой - притяжение между ядром одного атома и электронами другого, и наоборот. Два атома располагаются на таком межъядерном расстоянии, при котором эти силы точно уравновешены и энергия молекулы минимальна. Это расстояние называется равновесным re или длиной связи. Поведение связи при сжатии и растяжении можно сравнить с поведением пружины и предположить, что связь, подобно пружине, подчиняется закону Гука:
Существование устойчивой двухатомной молекулы можно считать следствием равновесия двух сил. С одной стороны, имеется отталкивание между положительно заряженными ядрами обоих атомов и между отрицательно заряженными электронными облаками, с другой - притяжение между ядром одного атома и электронами другого, и наоборот. Два атома располагаются на таком межъядерном расстоянии, при котором эти силы точно уравновешены и энергия молекулы минимальна. Это расстояние называется равновесным re или длиной связи. Поведение связи при сжатии и растяжении можно сравнить с поведением пружины и предположить, что связь, подобно пружине, подчиняется закону Гука:

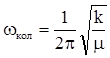 (Гц) (4.14)
(Гц) (4.14) (см-1)
(см-1) (Дж) v=0,1,2… (4.15)
(Дж) v=0,1,2… (4.15) (см-1)
(см-1) (Дж) (4.16)
(Дж) (4.16) (см-1)
(см-1)


