
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутреннее вращение в 1,2-дихлорэтане.Содержание книги
Поиск на нашем сайте
Изобразим энергетически самую выгодную транс-конформацию 1,2-дихлорэтана:
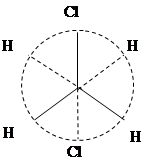 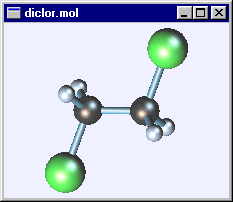 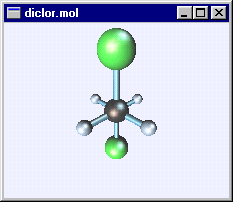
Фронтальный вид Вид справа Проекция Ньюмена
В этой конформации атомы хлора располагаются на максимально возможном расстоянии друг от друга и находятся в транс-положении относительно С-С связи. Поэтому этот конформер называется транс-конформером 1,2-дихлорэтана. Как видно из рисунков, проекция Ньюмена представляет собой схематическое изображение молекулы при взгляде вдоль связи С-С.
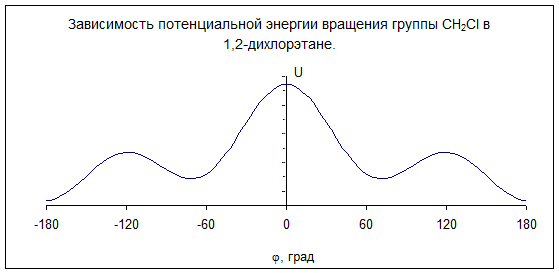
При вращении от 0о до 180о экстремальным точкам на этой зависимости соответствуют конформеры:
0o 60o 120o 180o гош+ (G+) транс (T)
При вращении в обратную сторону:
0o -60o -120o -180o = 180о гош - (G-) транс (T)
Таким образом, трем минимумам потенциальной зависимости U(j) соответствуют три конформера 1,2-дихлорэтана: T, G+ и G-. Когда говорят, что молекула 1,2-дихлорэтана имеет три конформера, то подразумевают именно эти конформеры, соответствующие минимумам зависимости U(j). На самом деле, молекула может принимать конформацию с любым значением угла j. Итак, существует бесконечно много конформеров 1,2-дихлорэтана. Каждый из них имеет некоторую потециальную энергию U(j). Однако, конформеры с мéньшей энергией встречаются в природе чаще, чем конформеры с бόльшей энергией в соответствии с распределением Больцмана. Если приближенно считать, что существуют только конформеры, энергия которых соответствует минимумам зависимости U(j) (дискретное распределение), то можно вычислить их больцмановское относительное распределение по формуле:
где Ni /Nmin – доля конформера с энергией Ui gi – степень вырождения конформера с энергией Ui (количество конформеров с одинаковой энергией U i)
Nmin, gmin, Umin – характеристики конформера с наименьшей энергией R - универсальная газовая постоянная (1,987 кал/моль•0C или 8,314 Дж/ моль•0C) Т – температура
Тема 2. Симметрия молекул. Представления о симметрии очень важны как в связи с теоретическим, так и экспериментальным изучением атомов и молекул. Основные принципы симметрии применяются в квантовой механике, спектроскопии и для определения структуры при помощи дифракции нейтронов, электронов и рентгеновских лучей. Некоторые расчеты значительно упрощаются, если принимать во внимание симметрию молекулы. Симметрией определяется также, может ли быть молекула оптически активной или иметь дипольный момент. Под операциями симметрии для молекулы подразумеваются операции отражения молекулы в плоскости, поворота молекулы как целого вокруг некоторой оси, отражение в центре, и, наконец, вращение вокруг некоторой оси с последующим отражением в плоскости. Этим операциям симметрии соответствуют элементы симметрии: плоскости симметрии, оси симметрии, центр симметрии и зеркально-поворотные оси симметрии.
Рассмотрим молекулу формальдегида H2CO. Эта молекула имеет две плоскости симметрии, при отражении в которых она не меняется. Первая вертикальная плоскость симметрии sv проходит через ядра всех атомов. Вторая вертикальная плоскость симметрии sv’ перпендикулярна первой и проходит через биссектрису угла HCH. При отражении ядра C и О сохраняют свои положения, а эквивалентные ядра Н меняются местами, что не связано с какими-либо изменениями в строении или свойствах молекулы. Ось симметрии n-го порядка (обозначается Cn ). Осью симметрии n-го порядка называется такая ось, при повороте вокруг которой на угол 360/n молекула не меняется. Рассмотренная выше молекула формальдегида помимо двух плоскостей симметрии имеет ось симметрии второго порядка C2, проходящую через линию пересечения плоскостей. При повороте 360/2=180о вокруг этой оси ядра С и О остаются на своих местах, а ядра Н меняются местами. Молекулы могут иметь ось симметрии следующих порядков: 1,2,3…6 и ∞.
Центр симметрии (обозначается i ).
Зеркально-поворотная ось симметрии n-го порядка (Sn).
Например, цис-конформер этана имеет ось симметрии C3 (она же – зеркально-поворотная ось S3), а также зеркальную плоскость, которая перпендикулярна оси С3 и обозначается sh. Эта плоскость отличается от плоскости для транс-конформера тем, что является зеркальной. Есть ли на этом рисунке центр симметрии?
Для транс-конформера этана имеется зеркально-поворотная ось шестого порядка, при повороте вокруг которой на 60о и последующем отражении в плоскости, изображенной на рисунке, молекула не меняется. Плоскость, изображенная здесь, не является зеркальной. Есть ли на этом рисунке центр симметрии?
Молекула может иметь несколько осей симметрии разных порядков. В этом случае одна из осей наивысшего порядка называется главной осью симметрии. Рисуют молекулу так, чтобы главная ось симметрии была расположена вертикально (см. рисунки). Здесь изображена проекция транс-конформера этана (вид снизу).
Группы симметрии. Все возможные сочетания элементов симметрии (операций симметрии), которые могут встречаться в молекулах, можно подразделить на строго определенное число групп симметрии. Следовательно, каждая молекула в соответствии с ее элементами симметрии, т.е. теми операциями, при которых она не меняется, может быть отнесена к определенной группе симметрии. Как найти группу симметрии какой-либо молекулы?
Во-первых, необходимо знать конфигурацию молекулы и зарисовать ее (лучше в нескольких проекциях).
Во-вторых, нужно найти все элементы симметрии этой молекулы: - начинать следует с поиска осей симметрии и выделения среди них главной оси симметрии; как только главная ось найдена, следует перерисовать молекулу, расположив главную ось вертикально - далее, нужно найти все плоскости симметрии и определить их тип sv, sh, или sd - наконец, отыскать зеркально-поворотные оси и центр симметрии. Следует отметить, что наличие у молекулы некоторых элементов симметрии обусловливает обязательное наличие и других элементов симметрии. Если молекула имеет две взаимно перпендикулярные плоскости симметрии, то линия пересечения этих плоскостей будет осью симметрии С2. Наличие оси С2 и плоскости, ей перпендикулярной, обусловливает наличие центра симметрии и зеркально-поворотной оси S2 и т.п.
В-третьих, по набору найденных элементов симметрии определить группу симметрии, пользуясь следующей таблицей.
Обычные точечные группы Шенфлиса.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 1498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.35.147 (0.01 с.) |

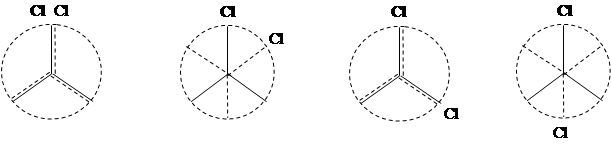
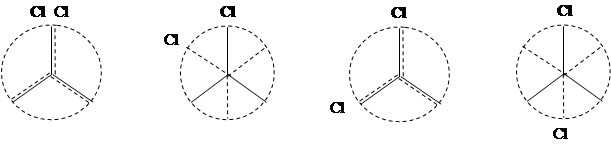
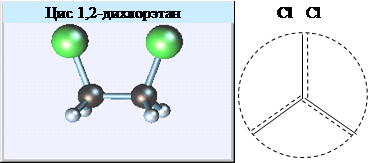 Конформация с максимальной энергией называется цис-конформацией, и, как легко догадаться, в этой конформации расстояние между атомами хлора минимальное. Очевидно, что путем поворота вокруг С-С связи можно прийти из цис-конформации в транс-конформацию. Примем угол поворота одной группы СH2Cl относительно другой за 0о в цис-конформации. Выбрав в качестве исходной цис-конформацию, будем вращать «дальнюю» группу СH2Cl, оставив при этом на месте «ближнюю» группу СH2Cl (атом хлора в ней выделен жирным). Тогда зависимость U(j) будет выглядеть следующим образом.
Конформация с максимальной энергией называется цис-конформацией, и, как легко догадаться, в этой конформации расстояние между атомами хлора минимальное. Очевидно, что путем поворота вокруг С-С связи можно прийти из цис-конформации в транс-конформацию. Примем угол поворота одной группы СH2Cl относительно другой за 0о в цис-конформации. Выбрав в качестве исходной цис-конформацию, будем вращать «дальнюю» группу СH2Cl, оставив при этом на месте «ближнюю» группу СH2Cl (атом хлора в ней выделен жирным). Тогда зависимость U(j) будет выглядеть следующим образом.
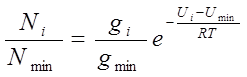 (1.1)
(1.1) Плоскость симметрии (обозначается s ).
Плоскость симметрии (обозначается s ). С∞ - любые углы поворота (линейные молекулы):
С∞ - любые углы поворота (линейные молекулы): Центром симметрии называется такая точка, при отражении в которой молекула не меняется. Например молекула этилена имеет центр симметрии на середине расстояния между ядрами углерода. При отражении в этой точке ядра углерода и ядра водорода (крест накрест) меняются местами, что не приводит к изменению в строении и свойствах молекулы.
Центром симметрии называется такая точка, при отражении в которой молекула не меняется. Например молекула этилена имеет центр симметрии на середине расстояния между ядрами углерода. При отражении в этой точке ядра углерода и ядра водорода (крест накрест) меняются местами, что не приводит к изменению в строении и свойствах молекулы. Это такая ось, при повороте вокруг которой на углы 360/n и последующего отражения в плоскости, перпендикулярной этой оси, молекула не меняется.
Это такая ось, при повороте вокруг которой на углы 360/n и последующего отражения в плоскости, перпендикулярной этой оси, молекула не меняется.
 Например, транс-конформер этана помимо главной оси симметрии C3 имеет еще три оси симметрии С2, изображенные на рисунке непрерывными линиями и проходящие через центр связи С-С. Как следствие, возникает еще одни элемент симметрии – плоскость симметрии sd. sd – это вертикальная плоскость, которая содержит главную ось C3 и делит ось С2 пополам. Таких плоскостей здесь три и они изображены пунктиром.
Например, транс-конформер этана помимо главной оси симметрии C3 имеет еще три оси симметрии С2, изображенные на рисунке непрерывными линиями и проходящие через центр связи С-С. Как следствие, возникает еще одни элемент симметрии – плоскость симметрии sd. sd – это вертикальная плоскость, которая содержит главную ось C3 и делит ось С2 пополам. Таких плоскостей здесь три и они изображены пунктиром.


