Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое распределение молекул по энергетическим состояниямСодержание книги
Поиск на нашем сайте
Молекулы всегда (кроме Т=0) находятся в тепловом движении и при соударениях обмениваются энергией, то есть осуществляется динамическое распределение молекул по всем возможным энергетическим состояниям. В равновесии справедлив статистический закон распределения Больцмана:
где N - общее число молекул Ni - число молекул в данном энергетическом состоянии с энергией E i gi - степень вырождения состояния с энергией E i (количество состояний с одинаковой энергией E i) k - постоянная Больцмана Т - температура Распределение молекул по состояниям обычно рассматривается как заселенность данного состояния по отношению к заселенности основного состояния, тогда абсолютноераспределение (4.5) принимает вид относительного распределения:
Если все состояния не вырождены (то есть все gi=1), то наиболее населены состояния с низкими энергиями. Если в (4.6) подставить (4.1) мы получим распределение молекул по колебательным состояниям. Соответствующая типичная диаграмма теплового распределения молекул по колебательным состояниям будет иметь вид:
Она показывает, как зависит относительная заселенность энергетических уровней от значения колебательного квантового числа v при различных температурах: при комнатной температуре (~300oK) заселенность состояний с v=1,2 и т.д. значительно меньше заселенности основного колебательного состояния (v=0), т.е. практически все молекулы при этой температуре находятся в основном колебательном состоянии. При повышении же температуры заселенность возбужденных колебательных состояний растет.
Если в (4.6) подставить (4.2), получим распределение молекул по вращательным состояниям (учтем, что gJ=2J+1 и g0=1):
Рассчитанное по этой формуле абсолютное распределение (общее число молекул принято за 100%) имеет вид:
Спектральные области. Электромагнитное излучение, связанное с переходами между электронно-колебательно-вращательными уровнями энергии молекулы, можно проиллюстрировать следующей таблицей. Для того чтобы падающее излучение могло вызвать эти переходы, они должны сопровождаться изменениями электрических свойств молекулы: либо должен изменяться электрический дипольный момент (см. области спектра излучения в таблице), либо должна изменяться поляризуемость молекулы (спектры комбинационного рассеяния).
1 100 104 106 108
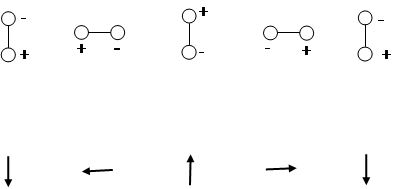
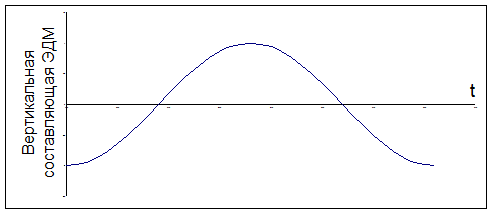
Рассмотрим, каким образом движение (молекулы, атомов или электронов), отраженное в таблице, приводит к изменению электрического дипольного момента. Микроволновая область. В полярной молекуле типа HCl один атом заряжен положительно, а другой отрицательно, т.е. молекула обладает собственным электрическим дипольным моментом. При вращении этой молекулы как целого вокруг собственного центра масс абсолютное значение дипольного момента останется, естественно, неизменным. Однако его направление будет изменяться во время вращения, и составляющая дипольного момента в некотором выделенном направлении будет испытывать регулярные изменения:
Эти изменения подобны изменениям электромагнитного поля: Поэтому благодаря своему вращению молекула будет взаимодействовать с излучением, поглощая или излучая при этом энергию, иными словами возникает вращательный спектр. Обо всех молекулах, имеющих собственный электрический дипольный момент, говорят, что они «активны в микроволновой области». Если же молекула не имеет собственного дипольного момента (H2, Cl2 и т.п.), то она «неактивна в микроволновой области». Таким образом, неполярные молекулы невозможно исследовать с помощью микроволновой спектроскопии. Инфракрасный диапазон (ИК спектры). Здесь изменение дипольного момента вызывается колебаниями атомов. В качестве примера рассмотрим молекулу двуокиси углерода CO2, имеющую линейную форму (почему?).
растянута
в равновесии
сжата Ясно, что в течение всего периода колебаний дипольный момент равен нулю и поэтому симметричное валентное колебание неактивно в ИК области. Однако имеется другое колебание – валентное асимметричное. При возбуждении этого колебания в молекуле CO2 одна связь СО связь сжимается, в то время как другая – растягивается:
Эта же молекула может совершать колебание еще одного типа – деформационное. Оно, как можно видеть, также активно в ИК области.
Сам факт проявления или не проявления в спектре определенных колебательных частот, соответствующих тому или иному типу колебаний, дает ценную информацию о структуре исследуемой молекулы.
Видимая и ультрафиолетовая области. Излучение или поглощение молекулами электромагнитных волн в этой области спектра связано с изменением электрического дипольного момента молекулы при возбуждении валентных электронов. Если же перераспределение электронной плотности происходит в результате возбуждения внутренних электронов, то появляется рентгеновский спектр.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 994; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.108 (0.008 с.) |

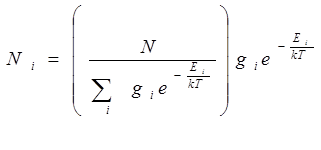 (4.5)
(4.5) (4.6)
(4.6)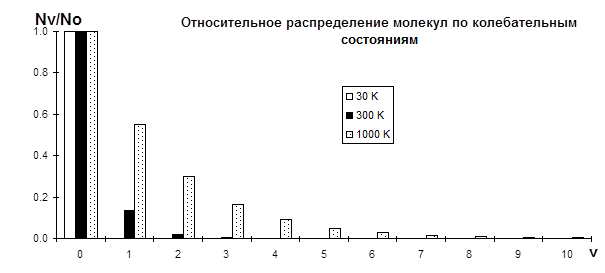
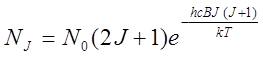 (4.7)
(4.7)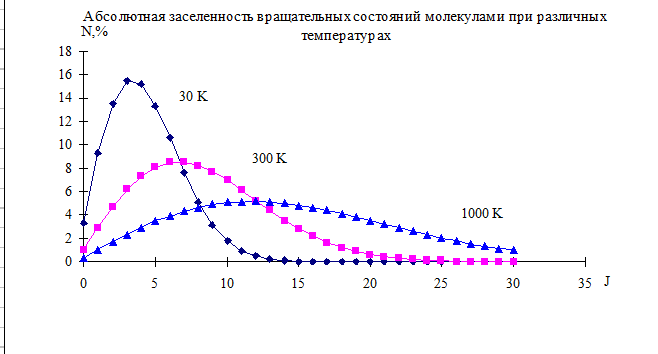 Мы видим, что это распределение имеет максимум. Это связано с тем, что вращательные состояния вырождены - степень вырождения 2J+1. С ростом температуры происходит сдвиг максимума в сторону больших значений вращательного квантового числа J - можно сказать, что происходит «перекачка» молекул из состояний с низкими энергиями в более высокоэнергетические состояния.
Мы видим, что это распределение имеет максимум. Это связано с тем, что вращательные состояния вырождены - степень вырождения 2J+1. С ростом температуры происходит сдвиг максимума в сторону больших значений вращательного квантового числа J - можно сказать, что происходит «перекачка» молекул из состояний с низкими энергиями в более высокоэнергетические состояния.
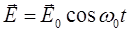 .
.
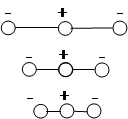 При возбуждении колебания, называемого симметричным валентным, молекула попеременно растягивается и сжимается так, что обе связи С-О изменяются синхронно:
При возбуждении колебания, называемого симметричным валентным, молекула попеременно растягивается и сжимается так, что обе связи С-О изменяются синхронно:
 Валентное асимметричное колебание активно в ИК области.
Валентное асимметричное колебание активно в ИК области.