
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полярные и неполярные молекулы. Дипольный момент и симметрия молекул.Содержание книги
Поиск на нашем сайте
Если центры положительных и отрицательных зарядов (см. предыдущий §) для равновесной конфигурации молекулы не совпадают, то молекула называется полярной и ее собственный дипольный момент отличен от нуля: Если же центры положительных и отрицательных зарядов в равновесной конфигурации молекулы совпадают, то молекула будет неполярной: Для равновесной конфигурации каждой молекулы существует определенная группа операций симметрии, при которых молекула, а, следовательно, и все характеризующие ее величины, не должны меняться. Рассматривая операции симметрии, свойственные той или иной молекуле, можно установить, имеет ли молекула собственный дипольный момент или нет, а если имеет, то куда он может быть направлен.
Если молекула имеет плоскость симметрии s, то при отражении в этой плоскости дипольный момент не должен менять ни абсолютного значения, ни своего направления. Это возможно только в том случае, если дипольный момент лежит в этой плоскости:
Если бы дипольный момент был направлен под углом к плоскости s, то при отражении он изменил бы свое направление в пространстве:
При повороте вокруг этой оси дипольный момент не должен изменить ни своего абсолютного значения, ни направления. Это возможно только тогда, когда дипольный момент направлен вдоль этой оси. Если бы дипольный момент был направлен под углом к оси, то при повороте он бы изменял направление:
Центр симметрии i.
Зеркально-поворотная ось симметрии Sn. Если молекула имеет зеркально-поворотную ось четного порядка, то дипольный момент такой молекулы равен нулю. Применим указанные правила к молекулам различного строения.
Двухатомные и линейные многоатомные молекулы. Эти молекулы имеют ось симметрии С∞, совпадающую с линией, соединяющей ядра. Следовательно, дипольный момент может быть направлен только вдоль линии, соединяющей ядра. Если других элементов симметрии нет, то дипольный момент отличен от нуля. Примеры: HF, H – C ≡ N, H – C ≡ C – Cl. Если линейная молекула имеет плоскость симметрии s, перпендикулярную к оси С∞, то m = 0. Действительно, с одной стороны m должен быть направлен вдоль С∞, а с другой – лежать в плоскости s. Единственное значение дипольного момента, удовлетворяющее обоим требованиям m = 0. Следовательно, линейные молекулы, имеющие оба указанных элемента симметрии, неполярны. Например, H2, O = C = O и т.п. Нелинейные трехатомные молекулы типа
Пирамидальные молекулы.
NH3, PH3... Плоские молекулы строения
BF3, AlCl3. Плоские молекулы строения
H2CO, H2CS.
Тетраэдрические молекулы. Имеют много элементов симметрии, но достаточно учесть четыре оси симметрии С3, направленные вдоль связей. Так как дипольный момент не может быть ориентирован сразу по четырем направлениям, то он равен нулю. CH4, SiF4. Итак, мы рассмотрели, каким дипольным моментом могут обладать молекулы различной симметрии. Однако не менее часто приходится решать обратную задачу: определять возможную симметрию и форму молекулы по измеренному значению дипольного момента. Например, если для молекулы YX3 известно, что ее дипольный момент равен нулю, то, очевидно, что их двух возможных конфигураций (плоской и пирамидальной) данная молекула имеет плоскую форму.
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 1066; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.96.202 (0.008 с.) |

 . Как пример можно привести полярные молекулы HCl, NH3, CH2=CHCl.
. Как пример можно привести полярные молекулы HCl, NH3, CH2=CHCl. . Это такие молекулы, как H2, BF3, CH4. Отсутствие собственного дипольного момента молекулы может быть следствием одной из двух причин: во-первых, обусловлено высокой симметрией молекулы, во-вторых, из-за случайной компенсации отдельных неравномерностей в распределении положительных и отрицательных зарядов в молекуле.
. Это такие молекулы, как H2, BF3, CH4. Отсутствие собственного дипольного момента молекулы может быть следствием одной из двух причин: во-первых, обусловлено высокой симметрией молекулы, во-вторых, из-за случайной компенсации отдельных неравномерностей в распределении положительных и отрицательных зарядов в молекуле. Плоскость симметрии s.
Плоскость симметрии s.

 Ось симметрии Cn.
Ось симметрии Cn. Если молекула имеет центр симметрии, то ее дипольный момент равен нулю. Иначе при отражении через центр симметрии дипольный момент менял бы свое направление на обратное:
Если молекула имеет центр симметрии, то ее дипольный момент равен нулю. Иначе при отражении через центр симметрии дипольный момент менял бы свое направление на обратное: Имеют только одну плоскость симметрии – это плоскость молекулы. Дипольный момент должен быть отличен от нуля, и лежать в плоскости молекулы. Например, FNO, ClNO и др.
Имеют только одну плоскость симметрии – это плоскость молекулы. Дипольный момент должен быть отличен от нуля, и лежать в плоскости молекулы. Например, FNO, ClNO и др.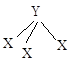 Имеют ось симметрии С3 и 3 плоскости симметрии s, проходящие через эту ось и направления связей. Дипольный момент не равен нулю и направлен вдоль оси С3.
Имеют ось симметрии С3 и 3 плоскости симметрии s, проходящие через эту ось и направления связей. Дипольный момент не равен нулю и направлен вдоль оси С3. Имеют ось симметрии С3 и плоскость симметрии sn, которая перпендикулярна C3. Следовательно,
Имеют ось симметрии С3 и плоскость симметрии sn, которая перпендикулярна C3. Следовательно,  Имеют ось С2 и две плоскости s, проходящие через эту ось. Дипольный момент не равен нулю и направлен вдоль оси.
Имеют ось С2 и две плоскости s, проходящие через эту ось. Дипольный момент не равен нулю и направлен вдоль оси.


