
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Содержательной процедуры «основного массива»Содержание книги
Поиск на нашем сайте Напомним, что выборочную процедуру «основного массива» применяют в тех случаях, когда генеральная совокупность неоднородна по стоимости составляющих ее элементов: в совокупности есть «основной массив» - элементы, стоимость которых превышает уровень существенности, установленный аудитором. Метод состоит в формировании выборки путем отбора этих элементов. Получим выражение для риска необнаружения Для этого проанализируем событие (назовем его событием А), вероятностью наступления которого является риск необнаружения - событие Б – аудитор в ходе проверки «основного массива» не выявил (просмотрел) содержащуюся в нем существенную ошибку; - событие В – аудитор не выявил существенную ошибку, поскольку она оказалась в «неосновном массиве», который аудитор счел возможным не проверять. Вероятность события В определяется объемом выборки (объемом «основного массива») – чем она больше, тем вероятность события В меньше. Поэтому в соответствии с определениями, которые введены федеральным стандартом аудита № 16 «Аудиторская выборка», вероятность события В – это риск, связанный с объемом аудиторской выборки (риск выборки RВ). Получим выражение для риска выборки RВ в нашем случае. Для этого введем следующие обозначения. Пусть N – объем генеральной совокупности (количество документов), N1 – объем «основного массива», N2 – объем «неосновного массива». Тогда N=N1+N2 .. Пусть J – стоимость документов генеральной совокупности (в рублях), J1 – стоимость документов «основного массива», J2 – стоимость документов «неосновного массива». Тогда J=J1+J2. Пусть S – уровень существенности (в рублях), «применяемый» для рассматриваемой генеральной совокупности; s = S/J * 100% - уровень существенности (в процентах). Допустим, что аудитор сформировал выборку объемом N1 и стоимостью J1 («основной массив») и проверил ее. Существенных ошибок в выборке при этом не обнаружено. Как мы указали выше, риск выборки RВ – это вероятность того, что в документах объема N2 может оказаться существенная ошибка, то есть ошибка, превышающая уровень существенности S. Если стоимость документов «неосновного массива» однородна и вариация ее незначительна (коэффициент вариации не превышает 30%), то можно оперировать средней стоимостью документа «неосновного массива» Тогда риск выборки RВ может быть определен, как вероятность следующего события: по крайней мере, М документов, принадлежащих генеральной совокупности N, будут полностью входить в объем N2 генеральной совокупности. Эта вероятность известным образом может быть определена по формуле Пуассона:
где p=M/N; N – объем генеральной совокупности; M – количество ошибок в генеральной совокупности; m – количество ошибок в выборке; n – объем выборки; R – вероятность появления случайной величины m, е=2,718 - основание натурального логарифма. В нашем случае объем выборки n=N1, количество ошибок в выборке m=0, отношение количества ошибок в генеральной совокупности к объему генеральной совокупности
Тогда формула Пуассона (3.32) преобразуется к виду:
Отношение N1/N обозначим n1 (n1=N1/N) – относительный объем «основного массива». Тогда
Графическая зависимость RВ от n1 для различных значений отношения Как видим, риск выборки RВ снижается с ростом объема выборки. При увеличении объема выборки (относительного объема «основного массива» n1) в 2 раза (с n1=0,1 до n1=0,2) риск выборки RВ от 15% (для Проиллюстрируем практическое применение формулы (3.34) на конкретном примере.
Рис.3.13. Зависимость риска выборки от относительного объема «основного массива»
Пример. Пусть аудитор проверяет состав дебиторской задолженности организации. Напомним, что несписанная дебиторская задолженность с истекшим сроком исковой давности или невозможная ко взысканию искажает как сальдо расчетов с дебиторами, так и прибыль от обычной деятельности. Дебетовое сальдо 62 счета составляет 5000 тыс. рублей. Допустимая ошибка S=100 тыс. рублей (s=2%). Данные аналитического учета: доля 10 дебиторов – 4700 тыс. рублей, доля 100 дебиторов – 300 тыс. рублей. Аудитор отбирает 10 дебиторов, задолженность которых составляет «основной массив», и подвергает их сплошной проверке. Существенных ошибок при этом не выявлено. Далее аудитор определяет количественную долю документов «основного массива» в генеральной совокупности n1=N1/N=10/110=0,09 (9%) и среднюю стоимость документа «неосновного массива» По формуле (3.34) для данных параметров генеральной совокупности риск выборки будет равен:
Из полученного результата аудитор может сделать обоснованный вывод, что вероятность появления существенной ошибки в документах «неосновного массива» мала, и их можно не проверять. В другом случае (например, при n1=9%, S=100000 руб. и
Вероятность появления существенной ошибки в «неосновном массиве» значительна, и аудитору следует подвергнуть его проверке.
Теперь получим выражение для риска необнаружения Выше мы определили, что применительно к процедуре «основного массива» риск необнаружения Поскольку события Б и В – несовместны, то в силу теоремы сложения вероятностей несовместных событий:
В силу определений, данных выше, вероятность события В (
Рассмотрим событие Б. Событие Б является результатом совместного появления двух событий (назовем их событиями Б1 и Б2). Событие Б1 – хотя бы один документ, содержащий ошибку, находится в «основном массиве». Событие Б2 – аудитор не обнаружил (просмотрел) находящийся в «основном массиве» документ, содержащий ошибку. Вероятность события Б1 обозначим
Вероятность события Б2 согласно данному выше определению – это риск Поскольку
Получаем выражение для риска необнаружения:
Рассмотрим практическое применение полученного выражения на примере.
Пример. Аудитор проверяет обоснованность предъявления НДС к вычету из бюджета. Объем генеральной совокупности составляет N = 500 счетов-фактур. Объём «основного массива» Средний НДС, приходящийся на один счет-фактуру из «неосновного массива»
Риск выборки:
Риск необнаружения:
Что же касается прочих выборочных процедур, использующих содержательные (нестатистические) методы (например, метод «блочного отбора», метод «ключевых элементов»), то применительно к ним отсутствуют данные, на основании которых можно было бы определить риски
|
||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 применительно к данному методу, то есть будем исходить из предположения, что генеральная совокупность содержит существенную ошибку, которую допустила бухгалтерия и не выявила служба внутреннего контроля.
применительно к данному методу, то есть будем исходить из предположения, что генеральная совокупность содержит существенную ошибку, которую допустила бухгалтерия и не выявила служба внутреннего контроля. , где
, где  , (3.32)
, (3.32)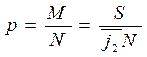 .
. =
=  . (3.33)
. (3.33) =
=  . (3.34)
. (3.34) приведена на рис.3.13.
приведена на рис.3.13. 2%.
2%.
 = exp (-n1 * S /
= exp (-n1 * S /  .. . Событие Б: аудитор не обнаружил существенную ошибку в «основном массиве», поскольку хотя бы один документ, содержащий ошибку находится в «основном массиве». Вероятность этого события обозначим
.. . Событие Б: аудитор не обнаружил существенную ошибку в «основном массиве», поскольку хотя бы один документ, содержащий ошибку находится в «основном массиве». Вероятность этого события обозначим  .
. . (3.35)
. (3.35) . (3.36)
. (3.36) . Поскольку вероятность
. Поскольку вероятность  - это вероятность противоположного события, то:
- это вероятность противоположного события, то: . (3.37)
. (3.37) .
. . (3.38)
. (3.38) . (3.39)
. (3.39) =20 счетов-фактур. Соответственно, объём «неосновного массива»
=20 счетов-фактур. Соответственно, объём «неосновного массива» 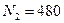 счетов-фактур. Сумма НДС, предъявления к вычету по всем счетам-фактурам, составляющим генеральную совокупность,
счетов-фактур. Сумма НДС, предъявления к вычету по всем счетам-фактурам, составляющим генеральную совокупность, 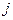 =6 000 000 руб. Сумма НДС по счетам-фактурам «неосновного массива»
=6 000 000 руб. Сумма НДС по счетам-фактурам «неосновного массива»  руб. Уровень существенности установлен аудитором в размере S = 120 000 руб. (2%). Риск
руб. Уровень существенности установлен аудитором в размере S = 120 000 руб. (2%). Риск  руб.
руб. .
.  (5%)
(5%)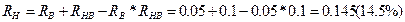
 без выделения его компонентов
без выделения его компонентов 


