
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочная вероятностно-статистическая процедура,
Основанная на биномиальном распределении количества ошибок В выборке Теперь рассмотрим статистический метод, основанный на биномиальном распределении случайной величины – количества ошибок в выборке. Введем следующие обозначения: N (в натуральных единицах) – объем генеральной совокупности; n (также в натуральных единицах) – объем выборки; m (в натуральных единицах) – количество ошибок в выборке (случайная величина); М (в натуральных единицах) – ожидаемая ошибка (ожидаемое количество ошибок в генеральной совокупности). Из теории вероятности известно, что случайная величина m при определенных условиях распределена по биномиальному закону, который может быть описан формулой Пуассона:
где p=M/N; M – количество ошибок в генеральной совокупности; R – вероятность появления случайной величины m; е=2,718 - основание натурального логарифма. Анализ формулы Пуассона показывает, что наиболее вероятное значение величины М для данного значения m определяется из выражения: M = m*N/n. (3.12) Пример. Аудитор проверяет счета-фактуры, полученные от поставщиков. Объем генеральной совокупности N=2500 счетов-фактур. Объем выборки n = 100 счетов- фактур. Количество ошибок (неправильно заполненных счетов-фактур) в выборке m = 2. Определим ожидаемую ошибку генеральной совокупности М.. Ожидаемая ошибка генеральной совокупности: M = m*N/n = 2* 2500/100 = 50 счетов-фактур. Метод, основанный на биномиальном распределении количества ошибок в выборке, безусловно, можно применять в тех случаях, когда аудитора интересует количество документов в генеральной совокупности, не соответствующих какому-либо признаку. Подобные процедуры, как было указано ранее, называют процедурой «на соответствие» (в отличие от процедур «по существу», когда аудитора интересует не количество ошибочных документов, а сумма ошибок в стоимостном выражении). Проверки «на соответствие» имеют место, например, при выявлении нарушений действующих в РФ законодательных и нормативных актов, которые могут и не повлиять на достоверность бухгалтерской отчетности, но которые своими последствиями могут нанести существенный ущерб проверяемому субъекту, государству или третьим лицам; при оценке аудитором надежности системы контроля в организации (контрольного риска); при оценке неотъемлемого риска.
При проверках же «по существу» аудитора интересует не количество ошибочных документов в генеральной совокупности, а денежная сумма ошибок. Метод, основанный на биномиальном распределении, может быть применен и в этом случае, но с определенными ограничениями. Если генеральная совокупность однородна (отсутствуют элементы, стоимость которых резко отличается от средней) и вариация стоимости незначительна (коэффициент вариации не превышает 20 – 30%), то денежная оценка ожидаемой ошибки К генеральной совокупности может быть получена из средней стоимости документа К=М*
Пример. Воспользуемся условиями предыдущей задачи (ожидаемая ошибка генеральной совокупности определена аудитором в размере М = 50 счетов-фактур). Пусть общая стоимость генеральной совокупности счетов-фактур (в части НДС) составляет J = 2 050 000 руб. Средняя стоимость документа (в части НДС)
Значение ожидаемой ошибки в рублях: К = М * Если генеральная совокупность неоднородна, т. е. содержит документы, стоимость которых резко (на порядок и выше) отличается от средней, то совокупность следует стратифицировать. Стратификация в данном случае заключается в отделении подобных документов. В результате этого достигается однородность генеральной совокупности, а выделенные из генеральной совокупности документы могут быть, в свою очередь, подвергнуты выборочной или (если их число невелико) сплошной проверке. Пример. Рассмотрим задачу с теми же исходными данными, что и в предыдущем примере: N = 2500 счетов-фактур стоимостью (в части НДС) — 2 050 000 руб. Генеральная совокупность неоднородна: стоимость 12 счетов-фактур в части НДС – 250 000 руб. (в среднем более 20 000 руб.). Стоимость 2488 счетов-фактур в части НДС — 1 800 000 руб. (в среднем около 700 руб.). Стратифицируем генеральную совокупность (отделяем 12 счетов-фактур с резко отличающейся стоимостью). Подвергаем их сплошной проверке. В результате этого выявляем один неверно оформленный счет-фактуру стоимостью в части НДС — 18 000 руб.
Страту объемом N = 2488 счетов-фактур подвергаем выборочной проверке. Объем выборки n = 100 счетов-фактур. Количество ошибок m = 2. Ожидаемая ошибка стратифицированной совокупности М = m *N/n = 2 * 2488/100 = 50 счетов-фактур. Средняя стоимость документа (в части НДС):
Тогда ожидаемая ошибка генеральной совокупности в рублях составит: К = 50 *· Полученное значение ожидаемой ошибки К аудитор сравнивает с заданным уровнем существенности S. Если К < S, то генеральная совокупность существенных ошибок не содержит . Рассмотренный выше метод может быть применен только в том случае, когда ошибочной является вся учетная сумма, проведенная по документу, что обычно имеет место при формальных ошибках, неправильном или безосновательном отражении операций, отражении незаконных операций и др. В других случаях (ошибки арифметические, пересчетные, в оценке, в расчетах и др.) ошибочная сумма обычно составляет какую-то часть учетной стоимости по документу, или даже может превышать ее. Применение метода, базирующегося на биномиальном распределении, в этом случае не имеет под собой серьезного статистического основания. Очевидно, в подобном случае более оправданным является применение метода, основанного на нормальном распределении размера ошибки. Известно применение рассмотренного выше метода, использующего в качестве элемента генеральной совокупности не натуральную единицу (документ), а денежную (рубль). Этот способ, в котором элементом совокупности является денежная единица (рубль), получил в литературе название «монетарного», практика применения которого изложена в ряде источников [7;21]. Рассмотрим его.
Монетарный» метод «Монетарный» метод основан на биномиальном распределении количества ошибок в выборке и состоит в следующем. Единицей совокупности (и генеральной, и выборочной), как мы уже сказали, в этом методе является рубль. Выборка при этом будет состоять из n рублей (на самом деле выборка будет состоять из n документов, но мы условно считаем, что элементом выборки является не документ, а рубль, входящий в стоимость этого документа[6]). Пусть в выборке, состоящей из n рублей (n «логических элементов»), m «логических элементов» содержат ошибочные суммы. Пусть К=
Пример. Аудитор проверяет авансовые отчеты (850 отчетов). Объем генеральной совокупности — N = 2 682 000 руб.(сумма, проведенная по всем авансовым отчетам). Объем выборки n = 50 руб. (содержатся в пятидесяти «логических элементах» — авансовых отчетах). Обнаруженные в выборке ошибки:
Среднее значение относительной ошибки
Ожидаемая ошибка генеральной совокупности К = Судя по ряду зарубежных источников [1; 4; 7; 21], «монетарный» метод достаточно популярен (во всяком случае, в литературе по аудиту). Между тем, анализ показывает следующее. В случае, когда размер ошибки не связан со стоимостью документа (например, ошибки в авансовых отчетах), применение «монетарного» метода не имеет достаточного статистического основания, поскольку отсутствуют какие-либо данные о характере распределения относительной ошибки В случае, когда размер ошибки связан со стоимостью документа (например, формальные ошибки в обязательных реквизитах счетов-фактур), размер относительной ошибки В заключение следует отметить, что применение статистических методов оправдано в тех случаях, когда генеральные совокупности состоят из элементов одного вида, в противном случае совокупность следует стратифицировать по виду элементов и определять ожидаемую ошибку как сумму ожидаемых ошибок страт (страты — совокупности, образовавшиеся в результате стратификации).
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.12.222 (0.028 с.) |
 , (3.11)
, (3.11) = J/N, где J (руб.) – общая сумма, проведенная по документам, составляющим генеральную совокупность:
= J/N, где J (руб.) – общая сумма, проведенная по документам, составляющим генеральную совокупность:
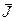 = 1 800 000/2 488 = 723 руб..
= 1 800 000/2 488 = 723 руб.. — стоимость i-го «логического элемента»,
— стоимость i-го «логического элемента»,  — ошибочная сумма в i-м «логическом элементе». Тогда
— ошибочная сумма в i-м «логическом элементе». Тогда  — относительная ошибка в i-м «логическом элементе». Но величину
— относительная ошибка в i-м «логическом элементе». Но величину  можно трактовать и таким образом:
можно трактовать и таким образом:  , по мнению авторов метода можно с помощью формулы (3.12) определить ожидаемую ошибку генеральной совокупности:
, по мнению авторов метода можно с помощью формулы (3.12) определить ожидаемую ошибку генеральной совокупности:
 N
N  (руб.). (3.14)
(руб.). (3.14)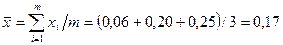 .
.


