
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Качественная оценка аудиторского риска с помощью метода нечетких множеств
Процедуры рассмотренных выше оценок могут быть формализованы применением метода, основанного на теории нечетких множеств. Рассмотрим возможность подобной формализации на примере оценки неотъемлемого риска Полное множество значений риска - низкий риск; - средний риск; - высокий риск. Введем понятие показателя степени риска G, принимающего значения от нуля до единицы. Соответствующее множеству - низкая степень риска; - средняя степень риска; - высокая степень риска. Далее построим классификацию текущего значения g показателя степени риска G, соответствующую разбиению этого множества на подмножества (табл. 3.9).
Таблица 3.9 Классификация текущих значений показателя степени неотъемлемого риска
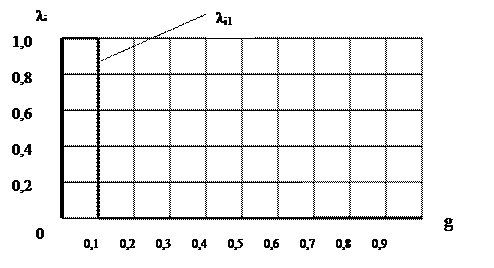
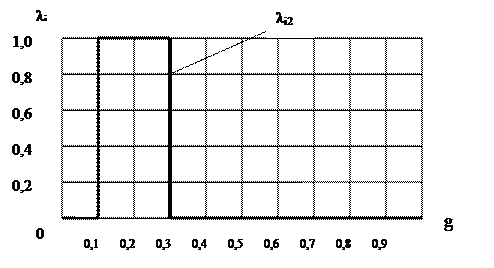
Построение указанной выше классификации осуществляется путем экспертной оценки (оценки аудитора) и в зависимости от его профессионального суждения может отличаться от варианта, предложенного в табл. 3.9. Далее введем следующие обозначения: Xi - анализируемый фактор, определяющий значение степени риска; N - количество факторов; i – текущий номер фактора (1 ≤ i ≤ N). Рассмотрим какой-либо фактор Xi, (например, «опыт и квалификация главного бухгалтера»). Принадлежность элементов нечеткого множества Xi определенному интервалу значений g (низкой, средней или высокой степени риска) установим с помощью функции принадлежности, областью определения которой является носитель g, а областью значений – единичный интервал [0,1]. В теории нечетких множеств обычно используют трапециевидные или треугольные функции принадлежности. В нашем случае целесообразно применение прямоугольных функций принадлежности, представленных на рис. 3.8, где λij - уровень принадлежности фактора Xi нечеткому подмножеству множества G (низкой, средней или высокой степени риска), j – номер подмножества (j = 1; 2; 3).
а)
б)
в)
Рис. 3.8 Функции принадлежности фактора Xi низкому риску – а), среднему риску – б), высокому риску – в)
Далее введем понятие коэффициента значимости каждого фактора, обозначив его ri. Путем экспертной оценки (т.е. на основании профессионального суждения аудитора) определим, равнозначны или неравнозначны выбранные нами факторы. Если факторы равнозначны, то коэффициенты значимости равны друг другу и могут быть определены из следующего выражения:
Если факторы неравнозначны, то их следует путем экспертных оценок проранжировать в порядке убывания их влияния. Тогда коэффициенты значимости факторов могут быть определены по правилу Фишберна:
где
Затем для каждого фактора Xi определяем λij – уровень принадлежности фактора интервалу значений g (низкой, средней или высокой степени риска). Текущее значение λij = 1, если согласно профессиональному суждению аудитора Xi принадлежит данному интервалу, и λij = 0 в противном случае. Далее определяем значение показателя степени риска g, исходя из полученных текущих значений λij и коэффициентов значимости факторов ri:
где gj - центральные значения показателя степени риска для каждого интервала: g1=0,05; g2=0,20; g3=0,65. Полученное из выражения (3.5) значение показателя степени риска g определяет подмножество Рассмотрим применение данного метода на конкретном примере.
Пример. Аудитор выделил пять факторов, определяющих по его мнению неотъемлемый риск, и проранжировал их в порядке убывания влияния:
Коэффициенты значимости факторов определены аудитором по формулам (3.3) и (3.4):
Результаты аудиторских процедур опроса, наблюдения, просмотра документов показали, что фактор X1 соответствует низкому риску (опытный главный бухгалтер); X2 – высокому (главный бухгалтер перегружен); X3 – среднему (документооборот организован на среднем уровне); X4 – высокому (нормативная база нестабильна); X5 – высокому (наличие сложных операций).
Исходя из полученных результатов, аудитор определил уровни принадлежности факторов:
Искомое значение показателя степени риска определяется по формуле (3.5):
По классификации текущих значений показателя степени риска (табл3.7) получаем значение Аналогичным образом может быть осуществлена качественная оценка контрольного риска Получив качественные оценки неотъемлемого, контрольного рисков и риска необнаружения, далее можно осуществить качественную оценку аудиторского риска, используя при этом полученные значения показателей степени риска g для рисков Таблица 3.10 Классификация показателя степени аудиторского риска
Пример. Из качественной оценки компонентов аудиторского риска ( С помощью этого метода может быть решена и обратная задача: оценка риска необнаружения, требуемого для обеспечения принятой оценки аудиторского риска. В том случае выражение (3.1) следует преобразовать к виду:
Тогда требуемое значение показателя степени риска Пример. Аудитор установил приемлемую оценку аудиторского риска: низкий риск. Из табл.3.8 получаем среднее значение показателя для низкого риска: g = 0,05. В процессе качественной оценки неотъемлемого и контрольного рисков получены численные значения их показателей: 0,40 и 0,50 соответственно. Тогда показатель степени риска необнаружения составит g = 0,05: (0,40 * 0,50) = 0,25. Из табл.3.7 получаем: риск необнаружения может быть средним.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.14.164 (0.012 с.) |
 .
.

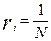 . (3.2)
. (3.2)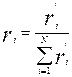 , (3.3)
, (3.3)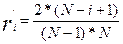 . (3.4)
. (3.4)

 , (3.5)
, (3.5) и риска необнаружения
и риска необнаружения  на уровне отчетности в целом.
на уровне отчетности в целом. с его компонентами. Для этого построим классификацию текущих значений показателя степени аудиторского риска, соответствующую разбиению
с его компонентами. Для этого построим классификацию текущих значений показателя степени аудиторского риска, соответствующую разбиению  .
.


