
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятностно-статистических процедурСодержание книги
Поиск на нашем сайте
При применении выборочных вероятностно-статистических процедур аудиторский риск проявляет себя как статистическая вероятность, и может быть численно определен исходя из закона распределения случайной величины (размера ошибок, либо количества ошибок в выборке). Как известно из статистики, при экстраполировании результатов исследования репрезентативной выборки на генеральную совокупность вероятность определяется объёмом выборки. Упомянутая статистическая вероятность при репрезентативной выборке зависит только от объема выборки, вследствие чего согласно федеральному стандарту аудита № 16 «Аудиторская выборка» ее следует определить, как риск выборки (риск, связанный с объемом выборки – будем обозначать его Таким образом, аудиторский риск RА на уровне сальдо и оборотов по счетам бухгалтерского учета при применении выборочных процедур, основанных на вероятностно- статистических методах, является функцией двух компонентов - риска выборки RВ и риска, не связанного с выборкой RНВ:
RА = f (RВ,RНВ). (3.20)
Получим выражения для риска выборки и аудиторского риска применительно к известным вероятностно-статистическим методам. Сперва получим выражение для риска выборки RВ применительно к процедуре, основанной на нормальном распределении размера ошибок. Риск выборки RВ является вероятностью события, заключающегося в том, что действительная ошибка Q генеральной совокупности окажется больше «применяемого» для данной генеральной совокупности уровня существенности S, в то время, как полученная аудитором ожидаемая ошибка К менее уровня существенности (Q> S при К< S). Заметим, что неравенство К< S может быть приведено к виду Получим выражение для риска выборки RВ. Для этого вспомним, что при нормальном распределении может быть определена верхняя граница доверительного интервала
где Вероятность R превышения генеральной средней Получаем следующее выражение:
Среднеквадратичное отклонение выборочной средней в выражении для доверительного интервала подсчитывается по известной зависимости:
где n- объем выборки; qi (руб.) – размер ошибки в i-ом элементе выборки. Тогда риск выборки RВ может быть найден из статистических таблиц по значению t, полученному из выражения для доверительного интервала:
Таким образом, для выборочной процедуры, основанной на нормальном распределении размера ошибки, риск выборки может быть найден из зависимости Пример. Воспользуемся исходными данными примера, рассмотренного ранее: объем генеральной совокупности N=850 авансовых отчетов общей стоимостью J=1 800 000 руб.; объем выборки n=50 авансовых отчетов; ошибки в авансовых отчетах, попавших в выборку: Средняя ошибка в выборке:
Ожидаемая ошибка генеральной совокупности: К= Среднеквадратичное отклонение выборочной средней:
Средний уровень существенности:
Расчетное значение предела интеграла Лапласа:
Из статистических таблиц [11] получаем, что при t =3,3 вероятность превышения генеральной средней верхней границы доверительного интервала равна 0,001. Таким образом, риск выборки RВ =0,1%. Из этого следует, что с вероятностью 99,9% ожидаемая ошибка генеральной совокупности (наиболее вероятное значение которой составляет 28 900 руб.) не превысит уровень существенности, равный 90 000 руб. Приведенные выше рассуждения основаны на предположении о том, что аудитор обнаружит в выборке все ошибки qi, то есть на предположении о том, что риск RНВ, определяемый опытом аудитора, его информированностью о клиенте и т.д., равен нулю. На практике, конечно риск RНВ >0, поскольку аудитор в силу различных причин (недостаток опыта, квалификации, усталость, небрежность и т.д.) может обнаружить не все ошибки в выборке. Введём понятие ошибки в выборке, обнаруженной аудитором – Вероятность обнаружения аудитором всех ошибок в выборке составит в таком случае Поскольку эта вероятность определяется всеми прочими факторами (опыт и квалификация аудитора, его добросовестность, знакомство с проверяемой организацией и т.д.), то вероятность противоположного события – это риск RНВ. Тогда:
Из выражения (3.14) получаем:
Риск RНВ может быть численно оценен путем анализа определяющих его указанных выше факторов, например, как это показано выше, с помощью линейной полиномиальной модели. Тогда аудиторский риск может быть определён из статистических таблиц, как функция
Пример. Используя исходные данные предыдущего примера, определим аудиторский риск, если значение RНВ =35%. Расчетное значение предела интеграла Лапласа:
Из таблиц [11] получаем, что при t =2,44 аудиторский риск RА =0,005 (0,5%).
Теперь получим выражение для риска выборки и аудиторского риска применительно к процедуре, основанной на биномиальном распределении количества ошибок в выборке. Ведем следующие обозначения: N – объем генеральной совокупности; n – объем выборки; m – количество ошибок в выборке; M – ожидаемая ошибка генеральной совокупности (ожидаемое количество ошибок в генеральной совокупности). Как мы указали ранее, в математической статистике показано, что для биномиального распределения наиболее вероятное значение величины М определяется из выражения M = m*N/n. В [11] показано также, что для отношения M/N может быть определена верхняя граница доверительного интервала a, которую величина M/N с вероятностью P = 1 – R не должна превысить:
где t – предел интеграла Лапласа; В [11] указано, что формула (3.28) является приближенной, но достаточной для практических расчетов при значениях n порядка сотен. Приравняв верхнюю границу доверительного интервала среднему уровню существенности
получаем значение предела интеграла Лапласа, определяющее риск выборки RВ:
где Используя тот же прием, что и при рассмотрении выборочной процедуры, основанной на нормальном распределении, получаем выражение для предела интеграла Лапласа, определяющего аудиторский риск:
Пример. Объем генеральной совокупности N=2500 счетов-фактур. Объем выборки n = 100 счетов- фактур. Количество ошибок (неправильно заполненных счетов-фактур) в выборке m = 2. Уровень существенности S =125 счетов- фактур (5%). Риск RНВ по оценке аудитора составляет RНВ =20%. Определим ожидаемую ошибку генеральной совокупности М, риск выборки RВ и аудиторский риск RА. Относительное количество ошибок в выборке:
Ожидаемая ошибка генеральной совокупности: M = m*N/n = 2* 2500/100 = 50 счетов-фактур. Средний уровень существенности:
Значение предела интеграла Лапласа, определяющее риск выборки:
При t =2,14 риск выборки составляет RВ =0,02 (2%). Значение интеграла Лапласа, определяющее аудиторский риск:
При t = 1,6 аудиторский риск составляет RА =5,5%.
Итак, мы получили выражения, с помощью которых можно количественно оценить компоненту аудиторского риска (риск выборки) как статистическую вероятность при выборочных проверках, основанных на нормальном либо биномиальном законах распределения случайных величин. Но количественная оценка риска выборки возможна ещё в одном случае – при использовании процедуры «основного массива». Покажем это.
|
||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.232 (0.011 с.) |

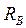 ). Следует отметить, что наряду со статистической вероятностью
). Следует отметить, что наряду со статистической вероятностью  ). Этот риск зависит от прочих факторов, не связанных с объемом выборки (опытом и квалификацией аудитора, его добросовестностью и пр.), и проявляет себя в рассматриваемом случае, как вероятность того, что аудитор может обнаружить в выборке не все имеющиеся в ней ошибки.
). Этот риск зависит от прочих факторов, не связанных с объемом выборки (опытом и квалификацией аудитора, его добросовестностью и пр.), и проявляет себя в рассматриваемом случае, как вероятность того, что аудитор может обнаружить в выборке не все имеющиеся в ней ошибки. <
<  , где
, где  - средний уровень существенности;
- средний уровень существенности; 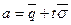 , которую генеральная средняя
, которую генеральная средняя 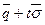 , (3.21)
, (3.21) - выборочная средняя;
- выборочная средняя; 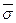 - среднеквадратичная погрешность выборочной средней; t – предел интеграла Лапласа..
- среднеквадратичная погрешность выборочной средней; t – предел интеграла Лапласа..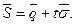 (3.22)
(3.22) . (3.23)
. (3.23) . (3.24)
. (3.24) , где значение предела интеграла Лапласа t определяется с помощью выражения (3.24). Рассмотрим возможность применения полученных зависимостей на примере.
, где значение предела интеграла Лапласа t определяется с помощью выражения (3.24). Рассмотрим возможность применения полученных зависимостей на примере. руб.,
руб., 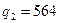 руб.,
руб.,  руб. Уровень существенности установлен аудитором в размере s=5% (S = 90 000 руб.). Определим ожидаемую ошибку генеральной совокупности К и риск выборки RВ.
руб. Уровень существенности установлен аудитором в размере s=5% (S = 90 000 руб.). Определим ожидаемую ошибку генеральной совокупности К и риск выборки RВ.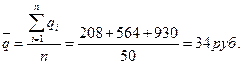
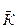 *N=34*850=28 900 руб.
*N=34*850=28 900 руб.
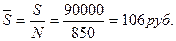

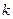 (руб.).
(руб.). , где
, где  - средняя ошибка в выборке, обнаруженная аудитором.
- средняя ошибка в выборке, обнаруженная аудитором.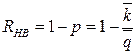 . (3.25)
. (3.25) . (3.26)
. (3.26) , где значение предела интеграла Лапласа определяется из зависимости:
, где значение предела интеграла Лапласа определяется из зависимости: . (3.27)
. (3.27)
 , (3.28)
, (3.28) - относительное количество ошибок в выборке.
- относительное количество ошибок в выборке. , (3.29)
, (3.29) , (3.30)
, (3.30) . (3.31)
. (3.31) .
.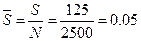 .
.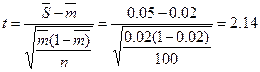 .
.



