
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адсорбция газов и паров на твердых адсорбентахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Общие определения. Способы выражения адсорбции Адсорбционные процессы на твердых поверхностях чрезвычайно широко распространены в различных отраслях народного хозяйства. Это, например, гетерогенный катализ, очистка газов и паров, хроматографический анализ и т.д. Поверхность твердого тела, на которой происходит адсорбция, называется адсорбентом. Адсорбирующееся вещество называется адсорбатом. Чаще всего твердый адсорбент – это либо капиллярно-пористые тела, либо высокодисперсные порошки с большой удельной поверхностью. Количество адсорбируемого вещества в состоянии адсорбционного равновесия определяется концентрацией вещества в обьеме, парциальным давлением компонента и температурой: A= f (C, P, T) – уравнение состояния адсорбционной системы в общем виде. Число параметров, определяющих состояние системы в адсорбционном равновесии можно рассчитать по правилу фаз Гиббса: C = K – φ + 2 Например: 1) твердый адсорбент – газ адсорбат K = 2; φ = 2; C = 2 A = f (P, T) 2) твердый адсорбент – адсорбат в растворе: K = 3; φ = 2; C = 3 A = f (C, P, T) Но если газообразных веществ нет, P = const, A = f (C, T). Способы выражения адсорбции: 1) Изотерма A = fT (c) или A = fT (P)
Наиболее распространена. 2) Изобара A = fP (T)
3) Изостера P = fA (T) или C = fA (T)
4) Изопикна A = fC (T)
Т3
А = const
C const C
Природа адсорбционных сил. Химическая и физическая адсобция. Поверхности твердых тел энегетически неоднородны, поэтому различные участки твердой поверхности обладают различной адсорбционной активностью. Химическая адсорбция происходит под действием сил химической природы и сопровождается образованием химических связей между атомами адсорбата и адсорбента. Пример: адсорбция О2 на угле и графите. Образуются поверхностные окислы:
Теплота хемосорбции 40 – 400 кДж/моль (того же порядка, что и тепловой эффект химической реакции). Хемосорбция – экзотермический процесс. Хемосорбция с большими значениями qa необратима. Она требует энергии активации. Скорость хемосорбции определяется уравнением V = V0exp[-Ea/RT] Еа – энергия активации адсорбции. Такая адсорбция называется активированной. Если хемосорбция не требует Ea, то адсорбция называется неактивированной. Центрами хемосорбции на кристаллической твердой поверхности чаще всего являются выступы, ребра, углы и вершины многогранников, т.к. атомы на них обладают ненасыщенными химическими связями, за счет чего создается большая локальная поверхностная энергия. Между молекулами адсорбата при хемосорбции преобладают силы взаимного отталкивания. Они обусловлены поляризацией молекулы адсорбата под действием большой локальной поверхностной энергии адсорбента. Дипольные молекулы адсорбата ориентируются параллельно и взаимно отталкиваются. Физическая адсорбция. При физической адсорбции действуют силы межмолекулярного взаимодействия 2-х типов между адсорбентом и адсорбатом: I) Силы притяжения II) Силы отталкивания I) Силы притяжения - это силы Ван–дер–Ваальса и водородной связи. Силы Ван-дер-Ваальса включают три вида взаимодействий: 1) ориентационное, 2) индукционное, 3) дисперсионное (наибольший вклад). Энергия притяжения зависит от расстояния между молекулами ΔUпр = - c/x6 (1) С = const На практике одна молекула адсорбата взаимодействует с несколькими молекулами адсорбента, поэтому энергия притяжения при адсорбции учитывает аддитивность дисперсионных сил: Uадд = - πcn/6x3 (2) n – число молекул в единице обьема адсорбента с = const Уравнение (2) использовано Лондоном для экспериментального докозательства дисперсной природы адсорбционных сил. II) При адсорбции действуют и силы отталкивания. Они определяются эмпирическим соотношением: Uот(x) = b/xm (3) b и m = const, обычно m = 12. Потенциальная энергия 2-х взаимодействующих атомов или молекул определяется уравнением Леннарда – Джонса: U(x) = b/x12 – c/x6 (4) Полная потенциальная энергия взаимодействия при адсорбции с учетом (2): U(x) = b/x12 – πcn/6x3 (5) Потенциальные кривые межмолекулярного взаимодействия при адсорбции имеют вид
- притяжение Точка минимума соответствует равновесию при адсорбции. Потенциальная энергия в точке минимума ≈ энергии адсорбции. 3. Теории адсорбции газов и паров твердыми адсорбентами Различные типы реальных адсорбционных систем не удается описать единым уравнением. Изотермы адсорбции, полученные экспериментально, можно свести, как правило, к одному из пяти основных видов изотерм. Поэтому и единой теории адсорбции до сих пор не существует. Мы рассмотрим несколько наиболее распространенных теорий, по мере их усложнения. I) Теория Ленгмюра Явилась фундаментальным вкладом в учение об адсорбции. Основные положения теории: 1. На поверхности адсорбента имеются активные центры, на которых происходит адсорбция. Таким образом адсорбция является локализованной. 2. Один центр адсорбирует одну молекулу. Адсорбционный слой является мономолекулярным. 3. Энергия адсорбции всех молекул одинакова (поверхность энергетически однородна). 4. Молекулы адсорбата не взаимодействуют между собой. 5. Адсорбция равновесна (число молекул, адсорбирующихся и десорбирующихся в единицу времени постоянно). 6. Время пребывания молекул в адсорбированном состоянии обратно пропорционально температуре. Адсорбция рассматривается как реакция квазихимического взаимодействия адсорбата и адсорбента:
Константа адсобционного равновесия: K = CAB/CA· CB CAB = A – адсорбция. СА = А∞ - А СА – Концентрация адсорбционных центров СВ – Концентрация вещества в растворе K = A/(A∞ - A)C A = A∞KC – AKC A(1+KC) = A∞KC Изотерма адсорбции Ленгмюра:
A = A∞ · Kc/1+Kc (1)
Для адсорбции газов и паров:
Константа адсорбционного равновевия K и Kp характеризует взаимодействие адсорбата и адсорбента (чем оно больше, тем больше K). Отношение А к емкости монослоя А∞ называют степенью заполнения поверхности: Θ = А/А∞ (3) Для нахождения констант уравнение Ленгмюра представляют в виде: 1/А = 1/А∞ + 1/А∞K · 1/Р Для оценки теорий адсорбции Брунауер предложил три критерия: 1. Уравнение изотермы должно правильно описывать экспериментальную зависимость А(Р). 2. Вычисленные константы должны иметь правдоподобные значения (в соответствии с их физическим смыслом). 3. Теория должна правильно отражать температурную зависимость адсорбции. Пранализируем теорию Ленгмюра по трем критериям: 1. Как правило, совпадение результатов опыта и теории наблюдается только при малых Р (или Θ) Линейная зависимость 1/А = 1/А∞ + 1/А∞K · 1/Р при больших Р нарушается. 2. А∞ экспериментальная меньше, чем А∞ вычисленная в предположении плотной упаковки молекул в слое. Ленгмюр это несоответствие обьяснил адсорбцией на отдельных центрах (а не сплошной слой), ввел понятие локализованной адсорбции. 3. А∞ зависит на практике от Т. Этого теория не учитывает. Ленгмюр предположил, что причиной этой зависимости является энергетическая неоднородность поверхности, но в рамки его теории это не укладывается. Таким образом, теория Ленгмюра не соответствует многим реальным системам, описывает только некоторые из них, и то в узком интервале Р. Но теория имеет огромное значение. Любая теория адсорбции при введении в нее упрощающих условий сводится к классической форме уравнения Ленгмюра. Это является одним из критериев оценки других теорий. Теория Ленгмюра, таким образом, имеет фундаментальный характер. Эта теория стала классической. II) Потенциальная теория Поляни. 1. Адсорбция нелокализована. 2. На поверхности адсорбента существует силовое поле, распространяющееся на значительное расстояние от поверхности. 3. Адсорбционный слой полимолекулярен. По нормали от поверхности плотнось адсорбционного слоя убывает. 4. Поверхность характеризуется адсорбционным потенциалом φ, убывающим по нормали от поверхности. φ = RT lnP0/P (1) φ – есть изотермическая работа сжатия пара при переводе его от равновесного давления P в обьеме фазы в поверхностный слой с давлением насыщенного пара P0 P0 – давление насыщенного пара адсорбата в адсорбционном слое. P – давление насыщенного пара адсорбата в обьемной фазе. Теория оказывается достаточно простой в том случае, если рассматривается адсорбция паров и состояние адсорбционного слоя считается жидким.
- - - - - - - - - - - - - Эквипотенциальные поверхности. - - - - - - - - - - - - -
V = A · M/d (2), где А – адсорбция, М – молярный вес, d – плотность вещества в жидком состоянии, V – заполненная часть обьема поля на 1г адсорбента По экспериментальной изотерме A = f(P) строят характеристическую кривую φ – V, пользуясь уравнениями (1) и (2).
или
V, мм3 Оказалось, что адсорбционный потенциал φ не зависит от температуры, dφ/dT = 0. Поэтому по одной экспериментальной изотерме можно сделать серию изотерм для любых заданных условий, используя теорию Поляни. Пересчет по формулам (1) и (2): A1 → V → A2 P1 → φ → P2 при этом должна быть известна зависимость d и P0 от T. Недостаток теории Поляни – нет аналитического выражения изотермы адсорбции. Теория Поляни позволяет вычислить величину адсорбции при любой температуре, если известна изотерма хотя бы при одной какой-нибудь T, что очень важно для практических задач. Проверка теории Поляни по трем критериям Брунауэра невозможна, т.к. нет уравнения изотермы. Только о третьем критерии есть смысл говорить. И он выполняется. Адсорбция на твердых поверхностях, как правило, не заканчивается при завершении монослоя. Особенно это относится к пористым адсорбентам, где при адсорбции паров часто наблюдается заполнение пор. Это явление можно рассматривать как конденсацию пара под действием поверхностных сил.
Все многообразие изотерм можно свести по классификации Брунауера к пяти основным типам:
Как видно из рисунков для большинства систем адсорбция полимолекулярна.
А P
0 1 P/Ps Первые попытки получения изотермы полимолекулярной адсорбции сделаны еще Ленгмюром. Современная форма уравнения полимолекулярной адсорбции на основе обобщения теории Ленгмюра предложена Брунаэром, Эмметом и Тэллером (теория БЕТ).
Процесс адсорбции тогда можно представить в виде последовательных квазихимических реакций:
Константы равновесия этих реакций: Kp = AAB/A0P K1 = AAB1/AABP K2 = AAB2/AAB1P … (2) Из уравнений (2) концентрации поверхностных комплексов: AAB = KpA0P; AAB1 = K1AABP = K1KpA0P2; AAB2 = K2AABP = K2K1KpA0P3;... (3) Примем, что взаимодействие между молекулами во всех слоях одинаково, тогда: K1 = K2... = KL = аж/Рn = 1/Ps (4) KL – константа конденсации пара аж – активность вещества в жидком состоянии Ps – давление насыщенного пара аж = 1 Введем обозначения: Kp/ KL = С; P/Ps = x (5) Введем (4) и (5) в (3): AAB = C/ PsA0P = A0Cx; AAB1 = KLA0CxP = A0Cx2; AAB2 = 1/PsA0Cx2P = A0Cx3... Общее число активных центров (емкость монослоя A∞): A∞ = A0 + AAB + AAB2 + AAB3… = A0 + A0Cx + A0Cx2 + A0Cx3... = = A0 [1+Cx(1+x+x2...)] Сумма членов геометрической прогрессии: 1+x+x2+...=1/1 – x A∞ = A0(1+Cx/1 – x) = A0(1+Cx – x)/(1 – x) (6) Величина адсорбции компонента В (т.к. на каждом центре 2В, 3В и т.д.): А = ААВ + 2ААВ2 + 3ААВ3…= A0Cx + 2A0Cx2 + 3A0Cx3…= = A0Cx(1+2x+3x2+...) (6a) Ряд (1+2x+3x2+...) – производная по х от предыдущей геометрической прогрессии, и его сумма = 1/(1 – х)2, поэтому: А=А0Сx/(1-x)2 (7) Из уравнения (6) выразим А0: А0 = А∞(1-x)/1+Сх – х (8) Подставим в уравнение (7) уравнение (8) и значение х = Р/Ps: А = А∞(1-x)Сх/(1+Сх-х)(1-х)2;
(9) – уравнение полимолекулярной адсорбции БЭТ. Оно является основным уравнением обобщенной теории Ленгмюра.
Физический смысл констант в уравнении БЭТ: А∞ - емкость монослоя. С = Kp/KL откуда RT lnC = RT ln Kp - RT lnKL = - ΔG Kp и KL – константы адсорбции и конденсации,поэтому константа С характеризует разность энергий Гиббса процессов адсорбции и конденсации, т.е. энергию Гиббса чистой адсорбции. KL= 1/Ps
Анализ уравнения БЭТ 1) при P/Ps<< 1 (малые давления) из уравнения (9) А = А∞С Р/Ps/(1 + Р/Ps) = А∞KpPsР/Ps/1+ KpPsР/Ps=А∞KpP/1+ KpP, т.е. уравнение БЭТ переходит в уравнение изотермы Ленгмюра. 2) при Р→0 дальнейшие преобразования приводят к уравнению Генри: А = А∞KpP 3) при с >1 с ростом Р/Ps числитель в уравнении (9) растет, знаменатель растет (за счет второй скобки), затем уменьшается за счет первой скобки (при Р/Ps ≈ 1). это приводит к S – образной изотерме; при С < 1 знаменатель уменьшается, изотерма имеет вид №III. Уравнение БЭТ представляют в линейной форме:
Р/Ps/А(1 - Р/Ps) = 1/А∞С + С – Р/Ps ·1/А∞С (10)
α
tgα = C – 1/А∞С 1/А∞С
Р/Ps
Уравнение БЭТ широко применяется для определения удельной поверхности адсорбента: А∞ находится из графика, затем определяют Sуд = А∞ · NA · ω ω – Площадь, занимаемая одной молекулой адсорбента. Теория имеет большое практическое значение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1007; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.185.207 (0.008 с.) |




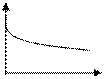
 Переход от одной функции к другой наглядно можно представить графически: A = fC(T) Т1
Переход от одной функции к другой наглядно можно представить графически: A = fC(T) Т1
 A
A Т2
Т2 Т4
Т4






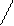 О О О О О О
О О О О О О




 U, +
U, +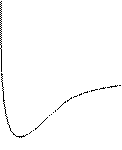 Кдж/моль отталкивание
Кдж/моль отталкивание ,нм
,нм



 A = A∞ · KpP/1+KpP (2)
A = A∞ · KpP/1+KpP (2) - - - - - - - - - - - - -
- - - - - - - - - - - - - //////////////////////////
////////////////////////// φ,
φ, кал
кал Дж/моль
Дж/моль









 В этом случае в области давлений, блихких к давлению насыщенного пара Ps адсорбция резко возрастает.
В этом случае в области давлений, блихких к давлению насыщенного пара Ps адсорбция резко возрастает.
 Дополнительным допущением к теории Ленгмюра здесь является возможность адсорбции двух, трех и более молекул на одном адсорбционном центре.
Дополнительным допущением к теории Ленгмюра здесь является возможность адсорбции двух, трех и более молекул на одном адсорбционном центре.



 А = А∞С Р/Ps/(1 - Р/Ps)[1+(C – 1)P/Ps] (9)
А = А∞С Р/Ps/(1 - Р/Ps)[1+(C – 1)P/Ps] (9)







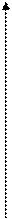 Р/Ps/А(1 - Р/Ps)
Р/Ps/А(1 - Р/Ps)


