
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адсорбция на границе жидкость-газ.Содержание книги
Поиск на нашем сайте
Адсорбцией называется изменение концентрации компонента в поверхностном слое, по сравнению с объемной фазой, отнесенное к единице площади поверхности. Единица измерения: моль/см2 или моль/м2. Мы встречались уже с этой характеристикой поверхностного слоя в предыдущем разделе, говоря о методе избыточных величин:
Гi – величина адсорбции компонента i, т.е. избыточное количество компонента i в поверхностном слое. Изучение адсорбционных явлений мы начинаем с наиболее простых систем: это молекулярная адсорбция на границе раздела жидкость-газ. Затем мы перейдем к рассмотрению адсорбции на твердых адсорбентах, и рассмотрим адсорбцию на границах раздела т/г и т/ж. В конце этой темы мы рассмотрим адсорбцию ионов, т.е. адсорбцию из растворов электролитов на твердых поверхностях. Такое разделение темы связано с рядом особенностей, присущих каждому типу систем. В то же время, наиболее общие закономерности, которые мы рассмотрим, присущи всем системам. Адсорбция- это явление поверхностное. Поэтому она оказывает большое влияние на свойства коллоидных систем, обладающих большой поверхностью раздела фаз. Уравнение адсорбции Гиббса. Рассмотрим границу раздела: газ-раствор этилового спирта в воде. Мы знаем, что поверхностное натяжение σ есть свободная поверхностная энергия единицы поверхности. Поэтому самопроизвольными будут являться такие процессы, которые снижают свободную поверхностную энергию, а следовательно и σ. σ спирта< σ воды, т.к. спирт менее полярная жидкость. Поэтому в водном растворе спирта будет происходить самопроизвольное концентрирование спирта из раствора на поверхности раздела жидкость-газ, что приводит к снижению σ. Возникающий градиент концентраций вызовет начало обратного процесса- диффузии. В результате установиться некоторое равновесное состояние, соответствующее минимуму энергии Гиббса этой системы. Для многих растворов в состоянии равновесия
Проинтегрируем уравнение (6.1) при постоянных интенсивных параметрах Т, σ, μ:
Продифференцируем уравнение (6.2), считая все параметры переменными:
Вычтем из (6.3) уравнение (6.1):
Или при Т=const, разделив на s:
Уравнение (6.5) представляет собой адсорбционное уравнение Гиббса в общей форме для плоского межфазного слоя. Для нашего случая, когда 1- растворитель (Н2О), а 2- растворенное вещество (С2Н5ОН), т.е. система двухкомпонентная, и при условии, что адсорбируется только растворенное вещество (компонент 2):
Так как
где а2- активность растворенного вещества, то:
Уравнение (6.9) тоже называется уравнением Гиббса. Оно используется для вычисления адсорбции компонента из раствора на однородной плоской поверхности. Для разбавленных растворов заменяют «а» на «с»- концентрацию:
Для адсорбции газов и паров на поверхности жидкости:
|
||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.12.236 (0.006 с.) |

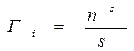
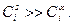 Запишем для состояния равновесия поверхностного слоя известное нам уравнение Гиббса:
Запишем для состояния равновесия поверхностного слоя известное нам уравнение Гиббса: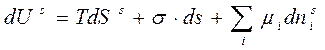 (6.1)
(6.1) (6.2)
(6.2)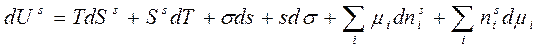
 (6.3)
(6.3)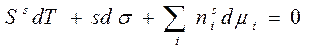 (6.4)
(6.4) , т.е.
, т.е. (6.5)
(6.5) , или
, или  (6.6)
(6.6)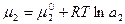 , (6.7)
, (6.7) , (6.8)
, (6.8)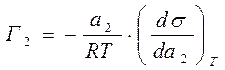 (6.9)
(6.9) (6.10)
(6.10)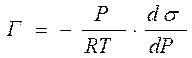 (6.11)
(6.11)


