
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория устойчивости гидрофобных коллоидов. (ДЛФО)Содержание книги
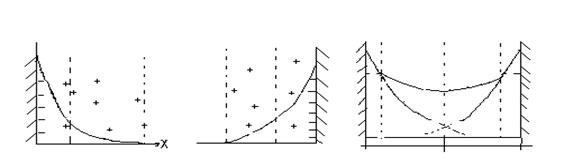
Поиск на нашем сайте Дерягин (1937-1941г.) совместно с Ландау. Не зависимо, но несколько позже Фервей и Овербек. Согласно теории ДЛФО, устойчивость коллоидного раствора определяется потенциальной энергией взаимодействия коллоидных частиц. U=Ur+ Uа Энергия взаимодействия 2 частиц имеет 2 составляющие: 1)энергия отталкивания Ur обусловленная электростатическими силами и 2) энергия притяжения Uа, обусловленная действием вандерваальсовых сил. Если Ur>0, то энергия положительна, если Uа < 0, то отрицательна. Преобладание 1ой из составляющих и определяет будет ли система устойчива. Рассмотрим подробнее действие этих сил. 1. Электростатические силы отталкивания Нам известно, что частицы в растворе, благодаря взаимодействию с дисперсной средой, заряжены одноименно. Представим себе 2 частицы сблизившихся на расстояние, меньшее толщины их двойного электрического слоя. Потенциал в этом случае не достигает нулевого значения при удалении от поверхности. Минимальное его значение на середине между поверхностями двух частиц (x=h). Суммарная кривая распределения потенциала между 2 частицами находится сложением 2 кривых распределения потенциала (1 и 2 частицы).j=2jх. То есть на расстоянии Х от каждой из 2ух взаимодействующих частиц в растворе, имеется отличный от нуля потенциал того же знака, что и на поверхности частицы. Это приводит к взаимному отталкиванию частиц (расклинивающему давлению p).
j0 j0 j0
j1 j1
х х Энергия отталкивания Ur является функцией расстояния между частицами.
Ur=2
Где С концентрация, х=1/2 расстояния между 2 частицами, j потенциал в данной системе, а g=(еZFj / 2RT-1) / (еZFj / 2RT+1). Анализ уравнения (2) показал, что силы отталкивания уменьшаются с ростом заряда z и концентрации ионов элемента, и с уменьшением электрокинетического потенциала φ1. Если φ1 = 0, то γ = 0. 2) Энергия притяжения обусловлена в основном действием сил Лондона – Ван-дер-Ваальса. Они действуют между молекулами независимо от их полярности и аддитивно складываются. В отличие от ориентационного и индукционного эффектов отдельных молекул, которые могут в значительной мере взаимно компенсироваться. Энергия притяжения между 2 частицами:
n – число атомов в единице объема частицы
h – постоянная Планка, ν0 – основная частота дисперсионного спектра колебаний атома, α – поляризуемость. Константа Гамакера А имеет порядок 10-12 эрг и слагается из отдельных констант, характеризующих когезионное и адгезионное взаимодействия. Она вычисляется квантово-статистическим путем. Суммарная энергия взаимодействия двух частиц в растворе:
Ur > 0, Ua <0. Зависимость Ur от Х экспоненциальная, Ua от Х - степенная. Тоесть притяжение медленнее ослабевает с расстоянием, чем отталкивание. Поэтому на больших расстояниях Х преобладают силы притяжения. При Х → 0, Ur → к const, а Ua → ∞ поэтому на малых расстояниях Х тоже преобладают силы притяжения. Изобразим кривые потенциальной энергии.
На средних Х может преобладать отталкивание. На построенной кривой – в этом случае 1 мах и 2 ямы (т.е. потенциальный барьер и 2 минимума). Возможность сближения частиц и коагуляции определяется высотой барьера и глубиной ям. Рассмотрим возможные варианты их соотношений: Случай. Если высота барьера и глубина II минимума невелики (<<kT), то частицы сближаются за счет кинетической энергии до наименьшего возможного расстояния (~ 5 Случай. Если высота барьера велика (>>kT), а глубина II минимума мала (≤ kT), частицы не могут преодолеть барьера и система агрегативно устойчива. Случай. Глубина II минимума достаточно велика (>>kT), происходит взаимодействие дальнего порядка (X~103 При этом частицы теряют свою подвижность, ввиду наличия сил притяжения, но коагуляции не происходит. При достаточной концентрации дисперсной фазы возможно превращение золя в полностью структурированную систему. Идея структурирования на основе дальнего взаимодействия выдвинута ранее Фрейндлихом и Лэнгмюром и позже теория доказана теорией ДЛФО. Большим достижением теории ДЛФО является и то, что она объясняет и подтверждает правило Шульце – Гарди. При подстановке условия быстрой коагуляции:
в уравнение для энергии (4), получим
Уравнение (5) представляет собой «закон 6-ой степени Дерягина», устанавливающий зависимость порога коагуляции от заряда иона С1 : С2 : С3 = 1: 64: 729 что хорошо согласуется с правилом Шульце – Гарди Теория ДЛФО используется чрезвычайно широко при исследовании устойчивости дисперсных систем. Развитием теории являются работы по 1. коагуляции смесью электролитов (аддитивное, антагонистическое, синергетическое действие), имеющие большое практическое значение. 2. по изучению гетерокоагуляции (теория взаимодействия между различными частицами)
|
||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 903; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

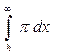 (1) Это уравнение выражает работу, необходимую для перенесения 2 частиц из ¥ на расстояние h от плоскости симметрии. Подставляя выражение для p, находят Ur. p=64g2сR T e-2kx, а Ur=((64сRT)/k)g2е-2кх(2). Из уравнения 2 параметр Дебая или обратная толщина диффузного слоя к=1/d (105-107 при изменении С от 10-5-10-1 и для Z=1).
(1) Это уравнение выражает работу, необходимую для перенесения 2 частиц из ¥ на расстояние h от плоскости симметрии. Подставляя выражение для p, находят Ur. p=64g2сR T e-2kx, а Ur=((64сRT)/k)g2е-2кх(2). Из уравнения 2 параметр Дебая или обратная толщина диффузного слоя к=1/d (105-107 при изменении С от 10-5-10-1 и для Z=1).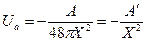 (3)
(3)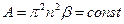 - константа Гамакера.
- константа Гамакера.
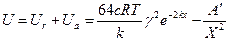 (4)
(4)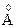 ). коагуляция происходит за счет ближнего взаимодействия частиц. Также системы не устойчивы, коагуляция необратима. Коагуляция может быть концентрационной (снижение высоты барьера вызвано увеличением с и k) или адсорбционной (уменьшением φ, в результате специфической адсорбции).
). коагуляция происходит за счет ближнего взаимодействия частиц. Также системы не устойчивы, коагуляция необратима. Коагуляция может быть концентрационной (снижение высоты барьера вызвано увеличением с и k) или адсорбционной (уменьшением φ, в результате специфической адсорбции).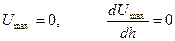
 (5)
(5)


