
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Манипулятора на основе сплайн – функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Планирование траекторий при ограниченном числе Опорных точек Наиболее общим случаем планирования траектории является рассмотрение траектории движения схвата из рабочей зоны одного оборудования в рабочую зону другого. При определении траектории должны быть учтены ограничения на саму траекторию и возможные препятствия на пути схвата. В качестве обязательных требований обычно выступают следующие. 1. В момент снятия объекта манипулирования движение схвата должно быть направлено перпендикулярно опорной поверхности ТО до тех пор, пока схват не уйдет на безопасное расстояние. Траектория от начальной точки 2. В момент постановки объекта манипулирования на ТО схват, начиная с некоторого безопасного расстояния, должен подходить перпендикулярно к опорной поверхности ТО. Точка В общем случае точки ухода и подхода, относящиеся к одному и тому же оборудованию, могут не совпадать из-за наличия или отсутствия объекта манипулирования в схвате, различных габаритов и условий транспортирования заготовок и т. д. 3. Между точками ухода и подхода схват движется в крейсерском режиме по траектории, оптимальной в том или ином отношении: по быстродействию; по затратам энергии; по условиям, обеспечивающим щадящий режим транспортирования объекта манипулирования. Например, могут быть ограничения на максимальные значения абсолютных скоростей и ускорений. Таким образом, в качестве наиболее общего случая будем рассматривать частную траекторию движения схвата от одной остановки до другой при его перемещении между соседними единицами ТО с выделением на ней трех характерных участков (участок ухода После привязки систем координат робота к системе координат ТО координаты точек
Рис. 12.1 Производственная сцена при планировании траектории
Планирование траектории манипулятора надо вести как в инерциальной системе координат робота, так и в системе его обобщенных координат. Учитывая, что управление манипулятором ведется в обобщенных координатах
где n – число звеньев манипулятора. Заметим, что такие точки должны быть определенны по каждой из 1,…,n обобщенных координат. Возможно несколько подходов к описанию траектории 1. Траектория на всем своем протяжении представляется одним полиномом по каждой обобщенной координате. 2. Каждый характерный участок траектории описывается отдельной сплайн-функцией. 3. На участках ухода 4. Участок Рис. 12.2
Задача планирования траектории схвата сводится, следовательно, к построению таких непрерывных или кусочно-непрерывных функций (рис. 12.2), которые бы проходили через указанные опорные точки и по возможности не намного отклонялись от прямой, соединяющей эти точки, т. е. к определению функций
Первый подход: обобщенные траектории описываются одним полиномом. Сформируем требования, которым должна отвечать траектория в этом случае.
1. Траектория на всем протяжении должна быть гладкой. 2. Траектория должна проходить через установленные характерные точки:
3. Скорости и ускорения схвата в начальной и конечной точках должны быть равны значениям, требуемым по условиям сопряжения схвата с технологической оснасткой. Обычно они равны нулю, однако, например, при работе с конвейером Эти требования позволяют записать граничные условия полиномов Точка Точка Точка Точка Таким образом, полином должен отвечать восьми граничным условиям и, следовательно, он должен быть минимум седьмой степени, когда в полиноме имеется восемь свободных коэффициентов. Если есть необходимость выполнения каких-либо дополнительных условий, степень полинома может быть повышена на одну – две. Однако в общем случае такое увеличение нежелательно, так как повышает степень непредсказуемости поведения траектории между опорными точками. Итак, рассмотрим полином седьмой степени.
Продифференцируем его дважды:
Подставим в эти выражения значения t = 0 для точки
Оставшиеся пять неизвестных коэффициентов должны быть определены по пяти неиспользованным граничным условиям из системы пяти уравнений:
Каждый из коэффициентов является функцией значений обобщенных координат опорных точек и моментов времени их прохождения, а именно:
Так как Описание траектории одним полиномом высокой степени весьма удобно с математической и алгоритмической точек зрения. Однако с физической точки зрения его использование может привести к нежелательным последствиям, а именно – к появлению эффекта «блуждания» схвата, т. е. к значительному отходу схвата от желаемой траектории между опорными точками.
Рис. 12.3. Общий вид полинома седьмой степени
В этом случае возникает сложная задача обеспечения приемлемых отклонений действительной траектории от желаемой, что можно осуществить, отступая от назначенных значений Второй подход. Чтобы уменьшить опасность нежелательного блуждания схвата, стремятся использовать полиномы возможно более низких степеней. Одним из путей понижения требуемой степени полинома является представление каждого из трех участков отдельными функциями, которые на границах участка должны быть соответствующим образом сопряжены – «склеены, сшиты». В результате траектория схвата будет представлена кусочно-непрерывной функцией, составленной из трех полиномов, которые в силу их взаимного сопряжения – «склейки» называют сплайн-функциями. Для рассматриваемой трехучастковой траектории с целью обеспечения плавного безударного перехода с одного участка на другой на границах участков значения функций, описывающих соседние участки, а также значения их первых и вторых производных должны быть равны друг другу. При рассмотрении сплайн-функций вместо абсолютного времени удобно использовать относительное (нормированное) время для каждого участка (рис. 12.4).
Рис. 12. 4
Установим граничные условия, которым должны отвечать сплайн-функции: Первый участок: Второй участок: 1) 2) 3) 4)
Третий участок:
Учитывая, что используются три полинома (по одному на каждом участке) и в каждом полиноме есть один свободный коэффициент, то сумма степеней полиномов должна быть равна 14 – 3 = 11 (здесь 14 – число граничных условий). Известны различные комбинации степеней полинома на участках. Наибольшее распространение получили: 4–3–4 – траектории, 3–5–3 – траектории, 5–2–4 – или 4–2–5 – траектории. Здесь цифры обозначают степени полинома на соответствующих участках. Чаще других используется 4–3–4 – траектория, так как из всех упомянутых она имеет полиномы более низких степеней. Запишем аналитическое выражение для 4–3–4 – траектории:
Используя условия 1, 2, 3 и 5, 9, найдем
Остальные девять коэффициентов определяются из решения системы девяти уравнений. Причем таких систем должно быть n, а определению подлежит Продифференцируем сплайн-функции при условии, что
Запишем по оставшимся девяти граничным условиям систему девяти уравнений: 1. Условие 4 ( 2. Условие 6 ( 3. Условие 7 ( 4. Условие 8 ( 5. Условие 10 ( 6. Условие 11 ( 7. Условие 12 ( 8. Условие 13 ( 9. Условие 14 (
Из решения этой системы девяти уравнений определяются девять неизвестных коэффициентов. Для еще большего уменьшения вероятности блуждания схвата используют сплайн-функции типа 3–3–3–3–3. В этом случае, кроме ранее рассмотренных трех участков, на участке
Рис. 12.5
В данном случае дополнительные участки вводятся именно с целью понижения степени составляющих сплайн-функции и уменьшения благодаря этому блуждания схвата. Конкретные значения обобщенных координат в этих точках не регламентируются, что позволяет уменьшить число граничных условий (назначаются лишь моменты времени t2 и t3 прохождения их схватом, т. е. моменты перехода с одной функции на другую). В данном случае также будем пользоваться понятием относительного (нормированного) времени. Запишем необходимые при указанных условиях граничные условия (сшивка полиномов должна обеспечить на границах участков непрерывность скоростей и ускорений, а также выполнение ранее принятых условий прохождения схвата через точки
Индекс i на время будем опускать.
Участок 1 Участок 3 Участок 5 1) 2) 3) 4) 19) Участок 2 Участок 4 20) 5) 6) 7) 14) Таким образом, получено двадцать граничных условий, что равно числу коэффициентов пяти полиномов третьей степени. Запишем сплайн-функцию для 3 – 3 – 3 – 3 – 3 – траектории:
Из условий 1, 2, 3, 5 и 15 определим
12.2. Общие случаи планирования траекторий В тех случаях, когда точки Возможны два варианта общих случаев (число участков равно М): Первый – когда координаты дополнительных точек не регламентируются как при рассмотрении 3–3–3–3–3 – траектории. Второй (наиболее общий случай) – заданы координаты всех промежуточных точек. Первый случай во многом аналогичен проектированию 3–3–3–3–3–траектории. Учитывая, что 1-й и (М-1)-й участки должны иметь по четыре ограничения, М-й – шесть ограничений, а все промежуточные по три ограничения, можно определить выражение для расчета суммы PМ степеней полиномов, удовлетворяющих сформулированным условиям: PМ = 4 + 4 + 6 + 3 (М – 3) – М = 5 + 2М (М > 3) Примеры: М = 3; PМ = 11 (4–3–4; 3–5–3; 5–2–3); М = 4; PМ = 13; М = 5; PМ = 15 (3–3–3–3–3); М = 6; PМ = 17; М = 10; PМ = 25 (3–3–2–3–2–2–2–3–2–3). Второй случай, как отмечалось, является наиболее общим случаем. Он возникает, когда траектория движения схвата является функцией времени и задана на всем протяжении в декартовых координатах манипулятора (рис. 12.6). Рис. 12.6
В результате решения обратной задачи кинематики находятся соответствующие заданным точкам значения обобщенных координат по каждой степени подвижности (рис. 12.7):
Рис. 12.7
Запишем ограничения для рассматриваемого общего случая с использованием понятия относительного времени:
Участок 1 Участок m 1) 2) 3) 4) ------------------------
Участок 2 Участок (М-1) 1) 2) 3) 4)
Участок 3 Участок M 1) 2) 3) 4) 5) 6)
Определим необходимую сумму степеней аппроксимирующих полиномов, учитывая, что на участке M имеется шесть условий, а на остальных по четыре. Pm= 6 + 4 (m–1) – m = 2 + 3m (m > 3)
Примеры: М = 3; PМ = 11 совпало с предыдущим, т. к. участков, вносящих разницу, в этом случае нет; М = 4; PМ = 14 (4–3–3–4); М = 5; PМ = 17 (4–3–3–3–4) два дополнительных условия по положению; М = 10; PМ = 32. Общим недостатком такого представления зависимостей
Таким образом, для успешного использования изложенных методов представления обобщенных координат необходимо иметь готовые таблицы зависимостей для расчета коэффициентов. В настоящее время таких таблиц нет. И для случая деления траектории на произвольное число участков их получение связано со значительными трудностями. Ограничения на обобщенные траектории. Законы движения Ограничения на обобщенные перемещения связаны с ограниченным диапазоном перемещения одного звена относительно другого (рис. 12.8)
Рис. 12.8
Для удовлетворения ограничений по перемещению следует определить экстремумы функций Ограничения на обобщенные скорости Ограничения на обобщенные ускорения определяются максимально возможными моментами сил и усилиями, развиваемыми приводами. Траектория движения схвата и его ориентации при конкретном рассмотрении может быть задана различным образом. В частности, она может быть задана, как и ранее, некоторым числом опорных точек при условии движения между ними с постоянными скоростями и по прямой линии. Приведем пример производственной сцены (рис. 12.9), в которой может возникнуть необходимость в прямолинейных движениях схвата. Понятно, что движение между опорными точками может осуществляться и по криволинейным траекториям. Рис. 12.9. Производственная сцена
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 765; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.182.15 (0.015 с.) |

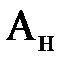 до точки
до точки 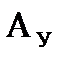 , находящейся на безопасном расстоянии, называется траекторией ухода, а сама точка
, находящейся на безопасном расстоянии, называется траекторией ухода, а сама точка  – точкой ухода (рис. 12.1).
– точкой ухода (рис. 12.1). , находящаяся на безопасном расстоянии при подходе к ТО, называется точкой подхода, а траектория от этой точки до конечной точки
, находящаяся на безопасном расстоянии при подходе к ТО, называется точкой подхода, а траектория от этой точки до конечной точки  – траекторией подхода (рис. 12.1).
– траекторией подхода (рис. 12.1). ; участок крейсерского перемещения
; участок крейсерского перемещения  ; участок подхода
; участок подхода  ) и четырех характерных точек:
) и четырех характерных точек:  ,
, 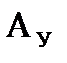 ,
,  ,
, – начальной, ухода, подхода и конечной. Координаты этих точек первоначально должны быть заданы в системе координат
– начальной, ухода, подхода и конечной. Координаты этих точек первоначально должны быть заданы в системе координат 


 j-го ТО.
j-го ТО.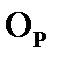


 робота.
робота. , то и окончательное планирование траекторий целесообразно вести именно в пространстве обобщенных координат. Следовательно, перед планированием траектории в обобщенных координатах робота должна быть решена обратная задача кинематики и по известным координатам точек
, то и окончательное планирование траекторий целесообразно вести именно в пространстве обобщенных координат. Следовательно, перед планированием траектории в обобщенных координатах робота должна быть решена обратная задача кинематики и по известным координатам точек  ,
,  ,
,  ,
,  должны быть определены соответствующие им значения обобщенных координат. В результате будут получены четыре опорные точки в системе обобщенных координат:
должны быть определены соответствующие им значения обобщенных координат. В результате будут получены четыре опорные точки в системе обобщенных координат: ,
, , в зависимости от предъявляемых к ней требований:
, в зависимости от предъявляемых к ней требований: и подхода
и подхода  для большей определенности она задается как функция времени в инерциальных координатах робота, например отрезком пространственной прямой. В этом случае траектория на этих участках строго определена и не подлежит планированию, а необходимо путем решения обратной задачи рассчитать соответствующие значения обобщенных координат и определить функции и
для большей определенности она задается как функция времени в инерциальных координатах робота, например отрезком пространственной прямой. В этом случае траектория на этих участках строго определена и не подлежит планированию, а необходимо путем решения обратной задачи рассчитать соответствующие значения обобщенных координат и определить функции и  .
. перемещения схвата от одного оборудования к другому с целью получения более определенной траектории разбивается на достаточно мелкие дополнительные участки, описываемые соответствующими сплайн-функциями.
перемещения схвата от одного оборудования к другому с целью получения более определенной траектории разбивается на достаточно мелкие дополнительные участки, описываемые соответствующими сплайн-функциями.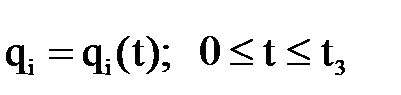 , (i = 1,…,n).
, (i = 1,…,n). .
. .
. , с помощью которых и будет реализовываться траектория.
, с помощью которых и будет реализовываться траектория.







 .
.
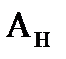 и получим
и получим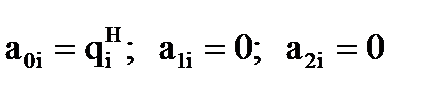 .
.
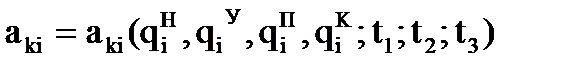 .
. , а i = 1,…,n, то всего должно быть определено
, а i = 1,…,n, то всего должно быть определено  коэффициентов, из них
коэффициентов, из них  коэффициентов из n систем пяти уравнений.
коэффициентов из n систем пяти уравнений.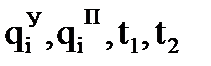 (будем считать, что начальные и конечные точки
(будем считать, что начальные и конечные точки  и
и  изменению не подлежат, так как они определяются расположением оборудования и конструкцией технологического приспособления).
изменению не подлежат, так как они определяются расположением оборудования и конструкцией технологического приспособления).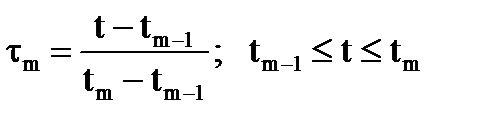 ;
;
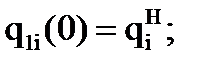 5)
5) 
 6)
6) 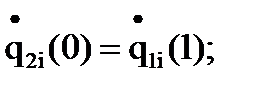
 7)
7) 
 8)
8) 


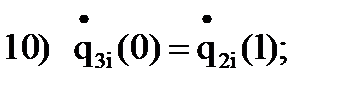





 коэффициентов, при этом коэффициенты полиномов, как и раньше, являются функциями обобщенных координат опорных точек и времени их прохождения.
коэффициентов, при этом коэффициенты полиномов, как и раньше, являются функциями обобщенных координат опорных точек и времени их прохождения. и
и


 ):
): 
 ;
;  ):
): 
 ;
;  ):
): 
 ):
): 
 ;
;  ):
): 
 ;
;  ):
): 
 ):
): 
 ):
): 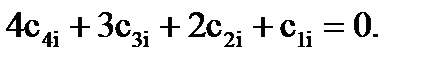
 ):
): 
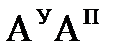 вводятся две дополнительные опорные точки и вместо этого одного участка возникает три (рис. 12.5).
вводятся две дополнительные опорные точки и вместо этого одного участка возникает три (рис. 12.5). ).
).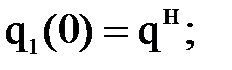 8)
8)  15)
15) 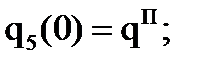
 9)
9)  16)
16) 
 10)
10)  17)
17) 
 18)
18) 


 11)
11) 
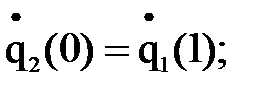 12)
12) 
 13)
13) 


 . Остальные коэффициенты определяются из системы пятнадцати уравнений.
. Остальные коэффициенты определяются из системы пятнадцати уравнений. и
и 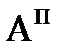 удалены друг от друга на значительные расстояния, может потребоваться большее число участков, чем три или пять. Увеличение числа участков может быть оправдано и в случае, если желательно обеспечить максимальную точность реализации траектории.
удалены друг от друга на значительные расстояния, может потребоваться большее число участков, чем три или пять. Увеличение числа участков может быть оправдано и в случае, если желательно обеспечить максимальную точность реализации траектории.


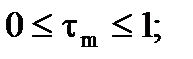
 . Здесь М – число участков траектории.
. Здесь М – число участков траектории. 1)
1) 
 2)
2) 
 3)
3) 
 4)
4) 
 1)
1) 
 2)
2) 
 3)
3) 
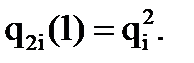 4)
4) 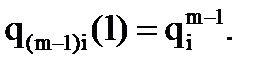
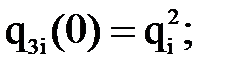 1)
1) 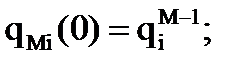
 2)
2) 
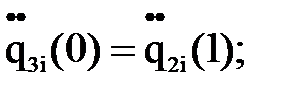 3)
3) 
 4)
4) 


 является необходимость предварительного решения системы большого числа уравнений для определения коэффициентов полиномов. Трудности усугубляются еще и тем, что при изменении числа участков появляется новая система уравнений, которую нужно решить заново.
является необходимость предварительного решения системы большого числа уравнений для определения коэффициентов полиномов. Трудности усугубляются еще и тем, что при изменении числа участков появляется новая система уравнений, которую нужно решить заново. , полученные в ходе планирования обобщенной траектории, реализуются приводами в соответствующих подвижных сочленениях. Полученные из теоретических соображений законы
, полученные в ходе планирования обобщенной траектории, реализуются приводами в соответствующих подвижных сочленениях. Полученные из теоретических соображений законы  должны быть проверены на возможность исполнения их соответствующим приводом. Существуют ограничения на перемещения, на скорости и ускорения.
должны быть проверены на возможность исполнения их соответствующим приводом. Существуют ограничения на перемещения, на скорости и ускорения.
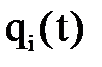 , что нетрудно выполнить после нахождения корней уравнения
, что нетрудно выполнить после нахождения корней уравнения  .
.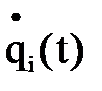 диктуются скоростными возможностями привода и его ограничениями на величину кинетической энергии. Для определения экстремальных значений
диктуются скоростными возможностями привода и его ограничениями на величину кинетической энергии. Для определения экстремальных значений  .
.


