
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная задача кинематики манипуляторов роботов
При контурном управлении Обратная задача кинематики манипуляторов является одной из основных задач кинематического и динамического анализа и синтеза манипуляторов. Она решается при контурном управлении роботом, когда схват должен перемещаться по заданной в пространстве и времени траектории, и заключается в определении значений обобщенных координат манипулятора по заданному положению схвата. В результате решения обратной задачи должны быть определены в аналитической или табличной форме зависимости
При работе манипулятора положение схвата непрерывно меняется по заданному закону движения. При этом центр схвата будет описывать требуемую траекторию, а схват будет ориентирован в пространстве вполне определенным образом, то есть обратная задача решается по заданным зависимостям
Примеры заданных траекторий: - раскрой листового материала (рис. 8.1а); - сварка непрерывных швов на сложной пространственной поверхности (рис. 8.1б).
Рис. 8.1. Движение схвата по заданной траектории
Для обеспечения произвольного требуемого положения схвата в общем случае необходимо шесть степеней подвижности, три из которых – переносные – должны обеспечивать заданное положение схвата в пространстве, то есть заданные значения координат
Если число степеней подвижности больше шести или больше заданных условий, то манипулятор приобретает свойство маневренности, в результате которой схват может занять требуемое положение при различных положениях промежуточных звеньев (рис. 8.2). Избыточные степени подвижности можно использовать для удовлетворения каких-либо дополнительных условий, например для обхода препятствий. В дальнейшем, если специально не оговорено, будут рассматриваться случаи, когда число степеней подвижности равно числу условий на движение схвата. Рассмотрим несколько простых случаев решения обратной задачи кинематики манипулятора.
Задано: n = 3; Определить: Непосредственно по рисунку 8.3 можно установить, что:
 Пример 2. Манипулятор с цилиндрической системой координат (рис. 8.4). Пример 2. Манипулятор с цилиндрической системой координат (рис. 8.4).
Задано: n = 3, x03(t), y03(t), z03(t). Определить: q1(t), q2(t), q3(t). По рис. 8.4 можно определить:
 Пример 3. Манипулятор с угловой (ангулярной) системой координат (рис. 8.5). Пример 3. Манипулятор с угловой (ангулярной) системой координат (рис. 8.5).
Задано: x02(t), y02(t). Определить: q1(t), q2(t). Данную задачу можно решить, как и раньше, из чисто геометрических соображений:
где:
Однако в этом случае может оказаться полезным и более общий подход, заключающийся в составлении уравнений, связывающих обобщенные и абсолютные координаты манипулятора, в частности такими уравнениями могут быть аналитические зависимости проекций характерных точек манипулятора. Запишем уравнения проекций характерной точки А2 схвата манипулятора на оси координат:
Решая эту систему уравнений относительно q1 и q2, можно определить требуемые законы движения по обобщенным координатам q1(t) и q2(t), уже в определенной степени абстрагируясь от конкретной схемы манипулятора. Два последних примера показывают, что даже для простейших манипуляторов определение требуемых по заданной траектории движения схвата законов изменения обобщенных координат может представлять определенные трудности. К настоящему времени прямого решения обратной задачи для манипуляторов общего вида не существует. В общем случае обратная задача кинематики манипуляторов решается алгоритмически, то есть численно.
Рассмотрим порядок решения обратной задачи с использованием методов нелинейного математического программирования, в частности одного из наиболее распространенных – градиентного метода. Нелинейное математическое программирование имеет следующий алгоритм: 1. Составляется или определяется критериальная функция как функция некоторых свободных параметров (в данном случае – как функция обобщенных координат). 2. Составляется штрафная функция, выражающая дополнительные условия проектирования, и также зависящая от свободных параметров (от обобщенных координат). 3. Составляется целевая функция, в состав которой входят определенным образом критериальная и штрафная функции. 4. Выбирается метод нелинейного математического программирования и в соответствии с ним составляется алгоритм оптимизации критериальной функции как части целевой функции. 5. Разрабатывается расчетная программа, и производятся расчеты до выполнения определенных условий. Изложим последовательность решения обратной задачи кинематики с использованием методов нелинейного математического программирования. Вернемся к выражению Каждая матрица Тогда матрица Т0n есть функция всех обобщенных координат и времени:
Следовательно, и каждый из шести наддиагональных элементов этой матрицы также является функцией всех обобщенных координат манипулятора
Пусть задан закон движения схвата, то есть заданы законы изменения его координат и углы ориентации:
Тогда можно записать матрицу-задатчик положений и ориентации схвата.
где
Положим, что в некоторый k-й момент времени tk (k = 0,…,K) заданное положение схвата:
то есть В следующий (k+1)-й момент времени tk+1 элементы Подставив эти новые значения в матрицу
Неравенство матриц
Значения обобщенных координат, при которых обеспечивается равенство матриц
После этого (k+1)-е положение принимается за k-е и задается очередное новое положение манипулятора, то есть в полученное равенство вновь вносится рассогласование, которое должно быть устранено после определения очередных значений обобщенных координат. Процесс продолжается, пока не будут определены значения обобщенных координат для всех требуемых К положений манипулятора на заданной траектории. Сформируем критериальную функцию. Так как целью решения является поиск таких значений обобщенных координат, при которых разность между заданным положением схвата и его фактическим положением равнялась нулю, то в качестве критерия следует принять параметр, отражающий эту разность. Например:
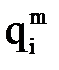 значение i-й обобщенной координаты на шаге m вычислительного процесса (рис. 8.7) в ходе поиска новых значений обобщенных координат; индекс П, здесь и в дальнейшем, опускается. Возможная траектория вычислительного процесса (штриховая линия) представлена на рисунке 8.7. значение i-й обобщенной координаты на шаге m вычислительного процесса (рис. 8.7) в ходе поиска новых значений обобщенных координат; индекс П, здесь и в дальнейшем, опускается. Возможная траектория вычислительного процесса (штриховая линия) представлена на рисунке 8.7.
Обобщенные координаты не могут принимать совершенно произвольные значения, так как перемещение по каждой степени подвижности может быть только в определенных границах (рис. 8.8): Рис. 8.8. Ограничения на движения манипулятора по обобщенным координатам
В связи с этим для автоматического выполнения возможного диапазона изменений обобщенных координат вводятся штрафные функции в виде следующих ограничений на значения qi:
где В качестве целевой функции можно использовать функцию, являющуюся суммой критериальной и частных штрафных функций:
Примем в качестве метода поиска новых значений обобщенных координат qi градиентный метод, выражающийся следующей зависимостью:
где Важно отметить, что в качестве первого приближения Вычислительный процесс приближения к значениям Учитывая характер функции (8.5), в качестве окончательного следует принять значение
Отметим, что (m+1)-й шаг к (k+1)-й точке в процессе вычислений может осуществляться по различным алгоритмам, свойственным методам нелинейного программирования. При использовании собственно градиентного метода (m+1)-й шаг должен осуществляться одновременно по всем координатам после определения направления движения по антиградиенту. Полученные значения
При выборе количества точек на заданной траектории возникает следующее противоречие: для более точного воспроизведения траектории желательно назначать как можно больше реперных точек, но это потребует и большего машинного времени для решения обратной задачи. При редком задании точек схват может отклоняться от заданной траектории на недопустимую величину. Таким образом, время, через которое следует назначать опорные точки, есть функция требуемой точности воспроизведения траектории. После определения в табличном виде функций Будем использовать для этого центральную разность. Тогда: Таким образом, будут получены функции
В результате будет получена непрерывная функция qi(t), которая в фиксированные моменты времени k гарантированно проходит через точки Пример. Пусть при t0 = 0с; t1 = 2с; t2 = 4с соответственно: Тогда:
Окончательно:
8.2. Решение обратной задачи кинематики манипуляторов Как известно, положение схвата манипулятора однозначно определяется его обобщенными координатами, а именно:
где:
Дифференцируя (8.6) по времени, получим
где В терминах рассматриваемой нами обратной задачи кинематики манипуляционных систем матрица Якоби (размерностью
Зависимость (8.7) более подробно можно представить следующим образом:
Зависимости (8.7) и (8.8) показывают, что между абсолютными скоростями
Выражение (8.7) представляет собой прямую скоростную задачу и её решение при известных (заданных) функциях Решим зависимость (8.7) относительно обобщенных скоростей
Эта зависимость и есть решение обратной задачи по скорости, которая часто используется для управления манипуляционным роботом в режиме on-line. При этом вектор обобщенных координат Q является неизвестным и значения В выражении (8.9) Рассмотрим более подробно последовательность решения прямой и обратной скоростных задач на примере простого манипулятора с двумя степенями подвижности (рис. 8.9).
Рис. 8.9. Манипулятор с двумя степенями подвижности
Прямая задача о положении:
При этом: Обратная задача о положении:
Даже для столь простого манипулятора решение обратной задачи представляет собой нелинейные зависимости. Для более сложных манипуляторов, как правило, найти зависимость Однако зависимость В то же время, как было указано раньше (см. зависимость (8.9)), между обобщенными скоростями Получим требуемые зависимости между обобщенными и абсолютными скоростями для рассматриваемого нами двухзвенного манипулятора, используя общий подход, не прибегая пока к обратной матрице Якоби. Пример решается с целью продемонстрировать порядок получения аналитических зависимостей для управления по скоростям, считая это решение обратной задачи в явном виде (подобно выражениям (8.11)) невозможным или нецелесообразным из-за сложности. Поэтому начнём решение с дифференцирования формул (8.10) по времени
Введем обозначения:
Тогда:
Решим полученные зависимости (8.13), (8.14) относительно обобщенных скоростей
Вычтем из первого выражения второе:
Для получения явной зависимости относительно
Вычитая из первого выражения второе, получим Откуда
Упростим выражения (8.15) и (8.16). Вначале упростим знаменатель дроби перед
Теперь выражения (8.15) и (8.16) можно записать в окончательном виде:
Или компактнее
В матричной форме выражения (8.17) имеют вид
Что и требовалось получить. Выражения для обобщенных скоростей в форме (8.17) и (8.18) выше получены обычным путем алгебраических преобразований. Для сложных манипуляторных систем такой подход будет связан с громоздкими преобразованиями. Для решения рассматриваемой задачи имеется более рациональный подход с использованием обратной матрицы Якоби. Представим производные (8.12) и (8.14) по времени в виде выражений:
или в форме матриц:
Матрица, являющаяся первым сомножителем в правой части выражения (8.19), есть матрица Якоби. Следовательно, выражение (8.19) можно записать в виде
Убедимся, что первый сомножитель в правой части выражения (8.20) есть матрица Якоби для рассматриваемого манипулятора.
Действительно, беря частные производные по
Данное выражение полностью совпадает с соответствующей матрицей выражения (8.19). Получим обратную матрицу Якоби в следующей последовательности: 1. Матрица алгебраических дополнений исходной матрицы Якоби:
2. Присоединенная матрица – транспонированная матрица алгебраических дополнений:
3. Определитель исходной матрицы Якоби – Якобиан:
4. Обратная матрица Якоби
Как видно, полученное выражение полностью совпадает с первым сомножителем правой части зависимости (8.18) и, следовательно, выражение (8.9) полностью обосновано для рассмотренного примера.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 2011; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.248.165 (0.103 с.) |
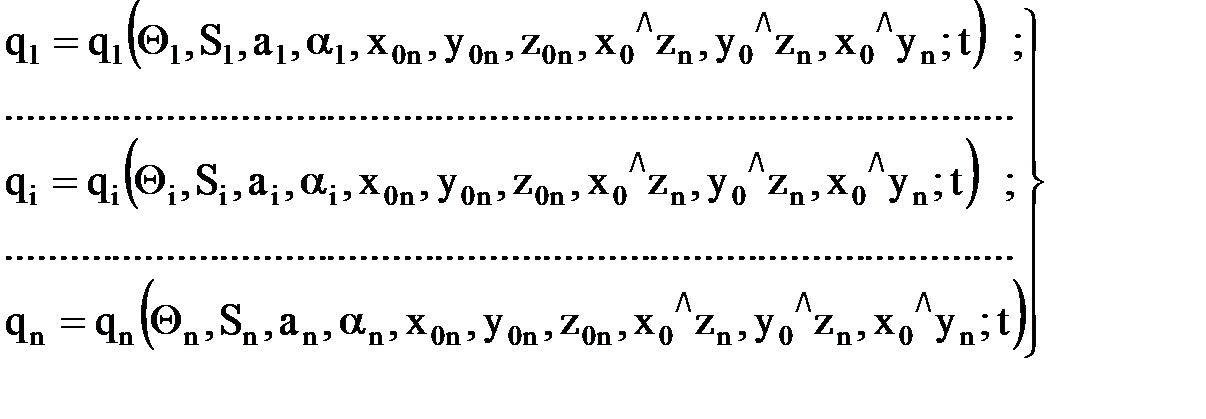
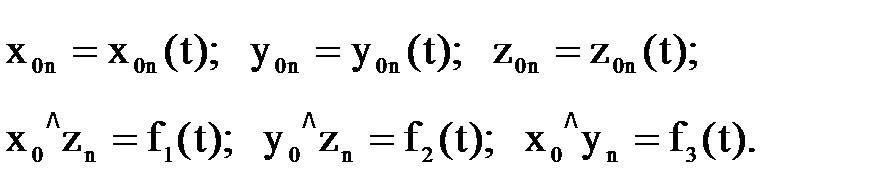


 а другие три – ориентирующие – заданную ориентацию схвата:
а другие три – ориентирующие – заданную ориентацию схвата: 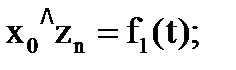
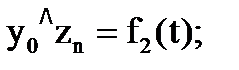
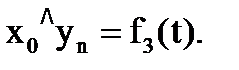




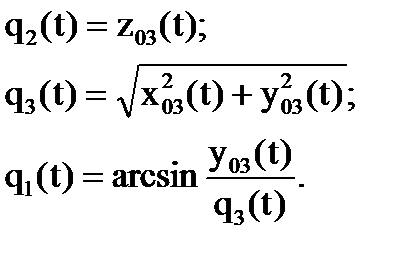

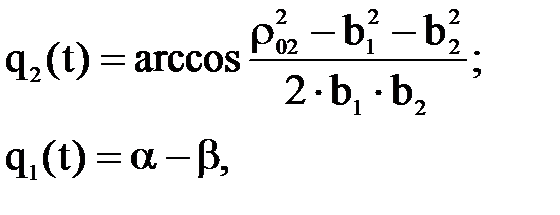

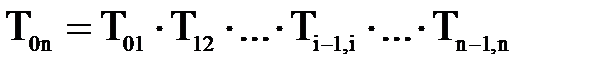 .
.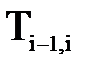 является функцией одной обобщенной координаты
является функцией одной обобщенной координаты 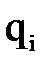 , которая в свою очередь, есть функция времени, то есть
, которая в свою очередь, есть функция времени, то есть 
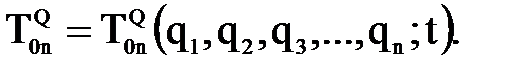
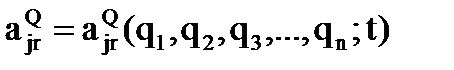 ,
, 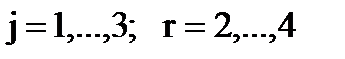 .
.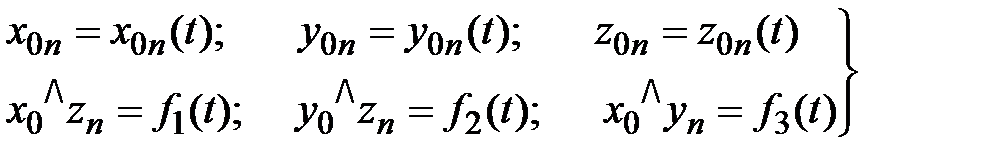 .
.
 ,
,
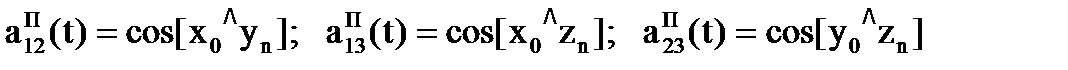 ;
;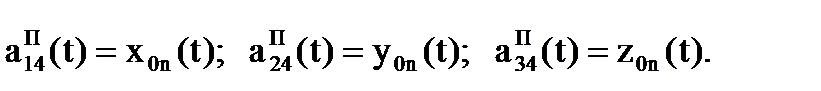
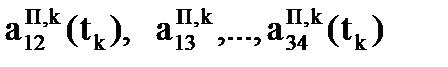 совпадает с фактическим его положением, обеспечиваемым текущими значениями
совпадает с фактическим его положением, обеспечиваемым текущими значениями 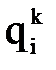 обобщенных координат.
обобщенных координат.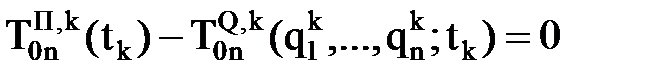 ,
,
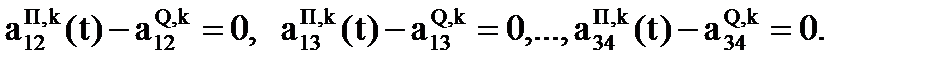
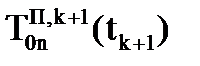 матрицы – задатчика (8.2) примут новые значения
матрицы – задатчика (8.2) примут новые значения 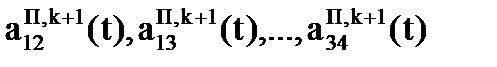 , рассчитанные по зависимостям (8.1).
, рассчитанные по зависимостям (8.1). выражения (8.3), получим
выражения (8.3), получим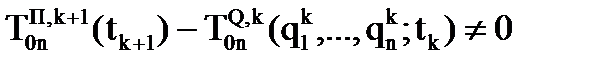 .
.
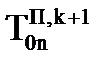 и
и 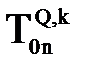 объясняется тем, что обобщенные координаты в матрице
объясняется тем, что обобщенные координаты в матрице  остались теми же, что были в момент tk.
остались теми же, что были в момент tk.
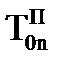 и
и  , принимается за значения
, принимается за значения  , соответствующие моменту времени tk+1.
, соответствующие моменту времени tk+1.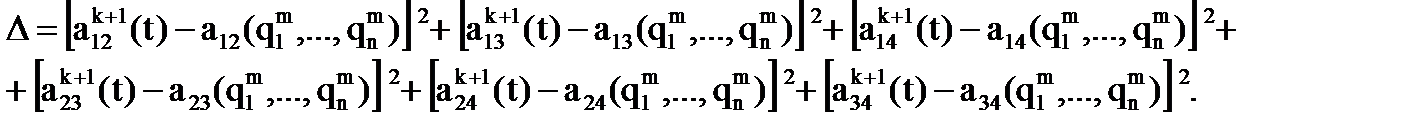

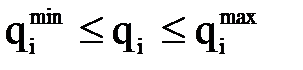 (i=1,…,n).
(i=1,…,n).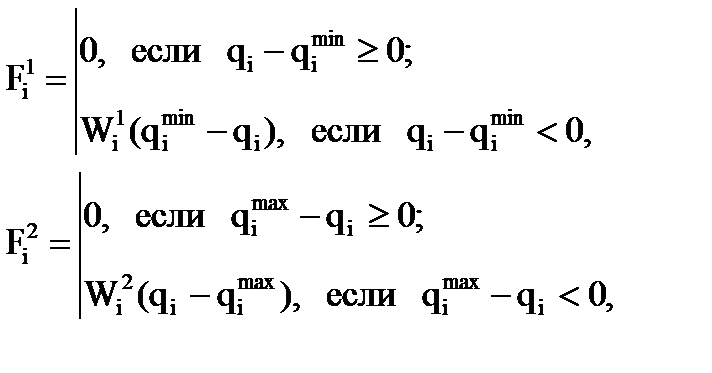
 ,
, 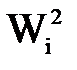 – весовые коэффициенты штрафных функций, которыми можно регулировать их крутизну. Кроме указанных могут быть и другие ограничения.
– весовые коэффициенты штрафных функций, которыми можно регулировать их крутизну. Кроме указанных могут быть и другие ограничения.
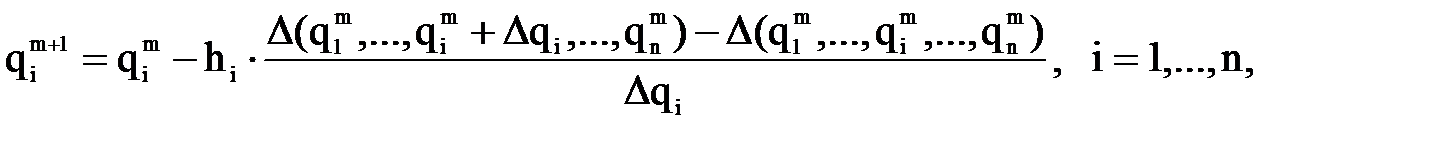
 – шаг по i-й обобщенной координате;
– шаг по i-й обобщенной координате; 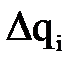 – малое приращение i-й обобщенной координаты, используемое при определении частной производной по qi.
– малое приращение i-й обобщенной координаты, используемое при определении частной производной по qi. используется старое значение
используется старое значение 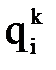 , то есть в начальный момент полагают
, то есть в начальный момент полагают 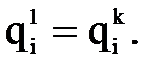
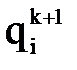 может быть прекращен по любому используемому в нелинейном программировании признаку. В частности, его можно закончить по условию
может быть прекращен по любому используемому в нелинейном программировании признаку. В частности, его можно закончить по условию  здесь
здесь 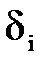 – допускаемая по точности воспроизведения траектории величина отклонений i-й обобщенной координаты.
– допускаемая по точности воспроизведения траектории величина отклонений i-й обобщенной координаты. .
. обобщенных координат соотносятся с моментом времени tk+1 и запоминаются. После этого в целевую функцию
обобщенных координат соотносятся с моментом времени tk+1 и запоминаются. После этого в целевую функцию  вместо значений
вместо значений  подставляются значения наддиагональных элементов, соответствующие моменту времени tk+2, которые и принимаются за
подставляются значения наддиагональных элементов, соответствующие моменту времени tk+2, которые и принимаются за  . Затем вновь запускается вычислительный процесс, который заканчивается, когда будут определены значения обобщенных координат для всех назначенных реперных точек k, k=0,...,K. В результате получается таблица значений обобщенных координат
. Затем вновь запускается вычислительный процесс, который заканчивается, когда будут определены значения обобщенных координат для всех назначенных реперных точек k, k=0,...,K. В результате получается таблица значений обобщенных координат 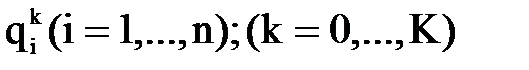 , которую можно трактовать как функции
, которую можно трактовать как функции 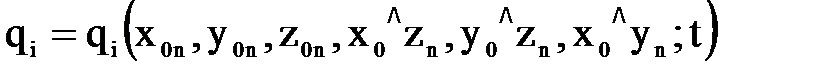 , являющиеся решением обратной задачи кинематики манипулятора и представленные в табличном виде.
, являющиеся решением обратной задачи кинематики манипулятора и представленные в табличном виде.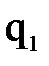

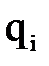



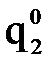
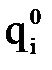
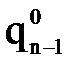

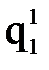

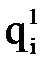
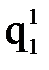
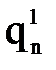
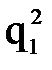

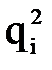


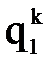
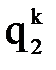

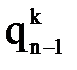
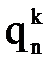
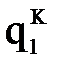
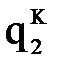
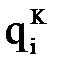
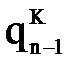

 можно численно их продифференцировать и найти обобщенные скорости и ускорения, возникающие в каждой степени подвижности при реализации заданной траектории движения схвата.
можно численно их продифференцировать и найти обобщенные скорости и ускорения, возникающие в каждой степени подвижности при реализации заданной траектории движения схвата.
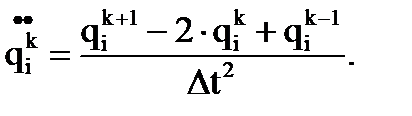
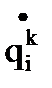 ,
,  также в табличном виде. Чтобы формировать управляющее воздействие в виде непрерывных функций, а не табличных, целесообразно аппроксимировать табличные значения обобщенных координат, скоростей и ускорений. Для этого можно воспользоваться, например, интерполяционной формулой Лагранжа:
также в табличном виде. Чтобы формировать управляющее воздействие в виде непрерывных функций, а не табличных, целесообразно аппроксимировать табличные значения обобщенных координат, скоростей и ускорений. Для этого можно воспользоваться, например, интерполяционной формулой Лагранжа:
 .
.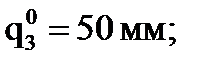
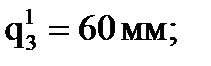
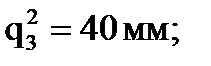
 .
.
 .
. ,
,
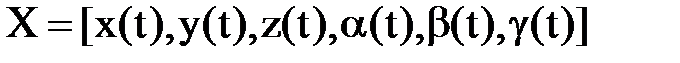 – вектор абсолютных координат схвата;
– вектор абсолютных координат схвата;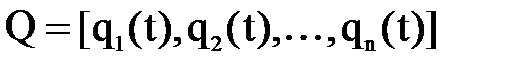 – вектор обобщенных координат манипулятора;
– вектор обобщенных координат манипулятора;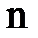 – число степеней подвижности манипулятора.
– число степеней подвижности манипулятора.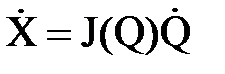 ,
,
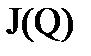 – матрица Якоби размерностью
– матрица Якоби размерностью 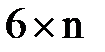 для преобразования (8.7).
для преобразования (8.7).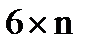 ) имеет вид:
) имеет вид:
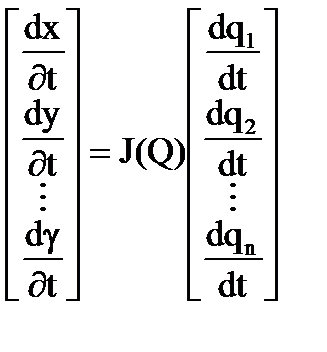
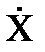 и обобщенными скоростями
и обобщенными скоростями 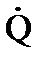 существует линейная связь, однако коэффициенты в этой линейной связи переменные, так как элементы матрицы Якоби
существует линейная связь, однако коэффициенты в этой линейной связи переменные, так как элементы матрицы Якоби 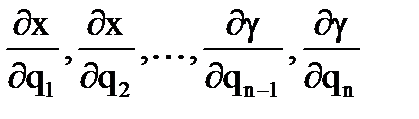 , которые образуют эти коэффициенты в различных сочетаниях, есть величины переменные.
, которые образуют эти коэффициенты в различных сочетаниях, есть величины переменные.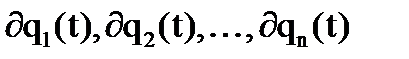 не представляет собой принципиальных трудностей.
не представляет собой принципиальных трудностей. , а именно:
, а именно: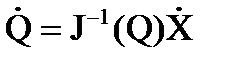
 приходится для данного момента времени (рассчитываемого момента реального времени) брать с датчиков обратной связи, фиксирующих текущее положение i-го звена относительно (i-1)-го, то есть значение
приходится для данного момента времени (рассчитываемого момента реального времени) брать с датчиков обратной связи, фиксирующих текущее положение i-го звена относительно (i-1)-го, то есть значение 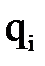 .
. есть обратная матрица по отношению к матрице Якоби
есть обратная матрица по отношению к матрице Якоби 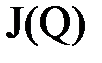 .
.
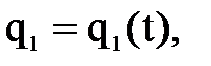
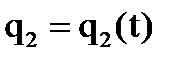 .
.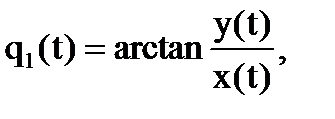
 .
.
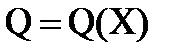 в явном виде не представляется возможным.
в явном виде не представляется возможным.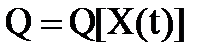 необходима для управления манипуляционным роботом, так как требуемое движение схвата обеспечивается соответствующими движениями звеньев манипулятора по обобщенным координатам:
необходима для управления манипуляционным роботом, так как требуемое движение схвата обеспечивается соответствующими движениями звеньев манипулятора по обобщенным координатам: 
 .
. и абсолютными скоростями
и абсолютными скоростями 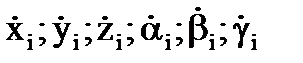 существует линейная связь с переменными коэффициентами. Именно поэтому часто и переходят к управлению по скоростям.
существует линейная связь с переменными коэффициентами. Именно поэтому часто и переходят к управлению по скоростям.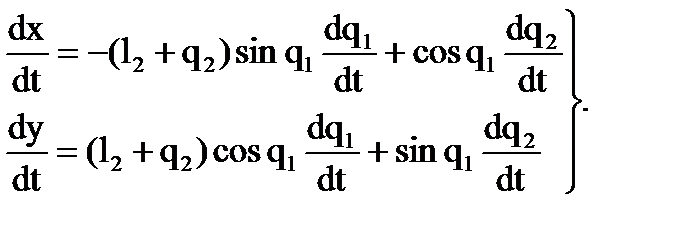
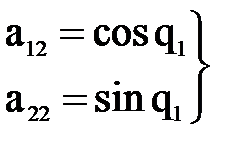
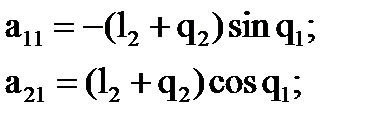
 ;
;  ;
; 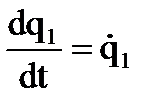 ;
; 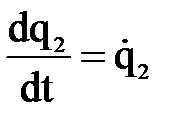 ;
;
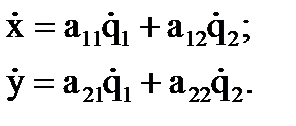
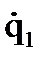 и
и 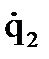 . Получим вначале явную зависимость от
. Получим вначале явную зависимость от 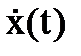 и
и  для обобщенной скорости
для обобщенной скорости 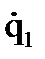 . Для этого умножим первую из зависимостей (8.14) на
. Для этого умножим первую из зависимостей (8.14) на 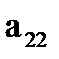 , а вторую на
, а вторую на 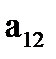 :
: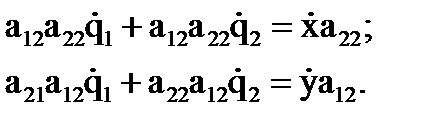
 , и следовательно:
, и следовательно: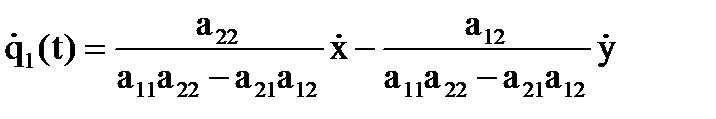 .
.
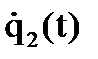 умножим первое из выражений (8.14) на
умножим первое из выражений (8.14) на 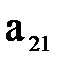 , а второе на
, а второе на 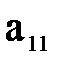 . Тогда:
. Тогда:
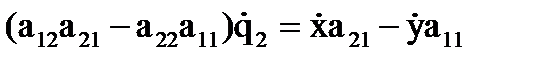 .
.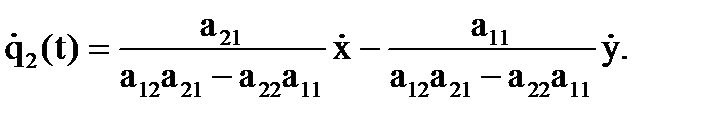
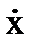 и
и  , учитывая выражения (8.13),
, учитывая выражения (8.13),
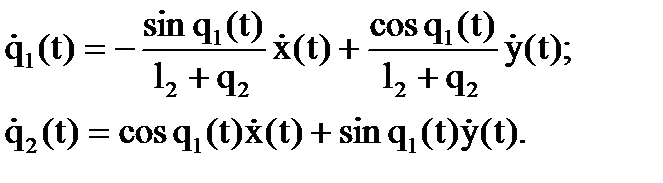
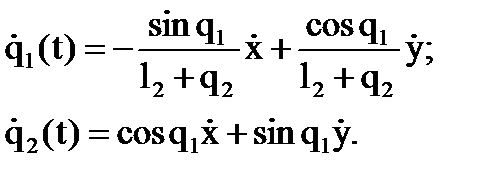
 .
.

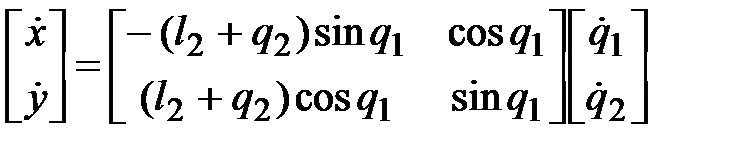
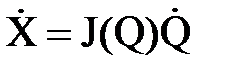 .
.
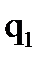 и
и  от правой части зависимости (8.10), получим
от правой части зависимости (8.10), получим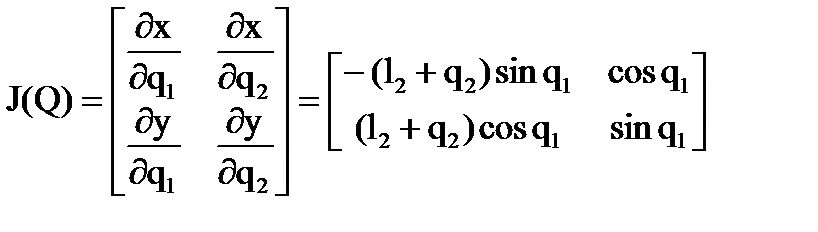 .
. .
.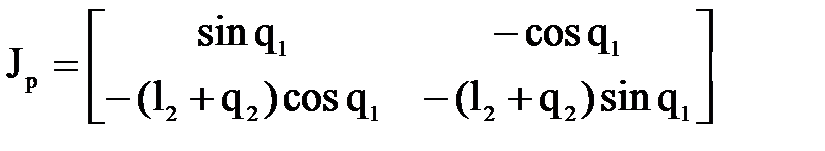 .
.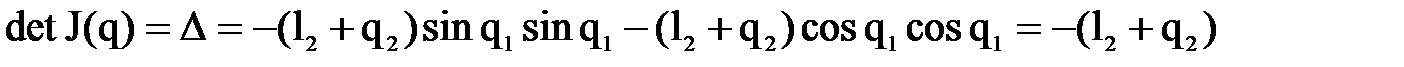 .
. .
.


