
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы кинематики манипуляторов роботов
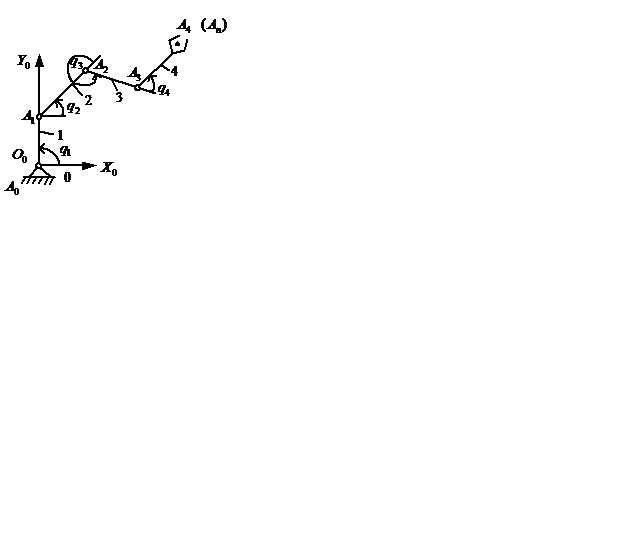
Для разработки методов расчета управляющих воздействий на звенья робота необходимо в начале установить кинематические зависимости между перемещениями звеньев манипулятора относительно друг друга при работе приводов и положением и ориентацией всех звеньев манипулятора в пространстве. Как известно, положение и ориентация схвата в пространстве определяется законами его движения относительно абсолютных (инерциальных) осей координат (рис. 6.5):
положение i-го звена относительно предыдущего (i-1)-го устанавливается с помощью обобщенной координаты qi (рис. 6.6):
Рис. 6.6
Следовательно, необходимо иметь математический аппарат, позволяющий установить для манипулятора любой конфигурации математическую модель его кинематики, которую в общем виде можно представить следующим образом: – для прямой задачи кинематики: – для обратной задачи кинематики:
Задачи подобного ряда сводятся к преобразованию координат. В общем случае для того, чтобы зафиксировать одну систему координат относительно другой необходимо шесть координат: смещение по трем осям и поворот вокруг этих осей. В связи с тем, что в манипуляторах роботов используются только одноподвижные вращательные и поступательные кинематические пары, для определения положения систем координат, связанных со звеньями манипулятора, достаточно четырех специальных координат. При этом сами системы координат должны быть связаны со звеньями манипулятора вполне определенным образом. Специальные системы координат манипуляторов были предложены американскими учеными И. Денавитом и Р. Хартенбергом в 1955–1960 гг. Изначально они предназначались для задания осей кинематических пар пространственных механизмов с низшими парами. В последние десятилетия эта координатная система была применена к описанию кинематики манипуляторов. Это связано с тем, что манипуляторы с одноподвижными вращательными и поступательными парами обладают рядом регулярных особенностей, хорошо согласующихся со свойствами координатной системы Денавита-Хартенберга.
 Введем ряд правил расположения осей и начал координат специальной системы координат относительно кинематических пар и звеньев манипулятора. Введем ряд правил расположения осей и начал координат специальной системы координат относительно кинематических пар и звеньев манипулятора.
Пронумеруем кинематические звенья от неподвижного звена до наиболее удаленного, на котором закреплен схват, присвоив им соответственно номера от 0 до n (рис. 6.7), где n – число подвижных звеньев манипулятора. Обозначим кинематические пары символом Аi, нижний индекс которого равен меньшему из номеров звеньев, образующих кинематическую пару. Например, кинематическая пара А1 соединяет кинематические звенья 1 и 2, а кинематическая пара А3 – кинематические звенья 3, 4 и т. д… Введем понятие оси zi i-й кинематической пары. Осью zi i-й вращательной кинематической пары, соединяющей i-е звено с (i+1)-м является ось шарнира кинематической пары. Эту ось будем считать принадлежащей i-му звену и жестко с ним соединенной. Именно вокруг этой оси вращается (i+1)-е звено относительно i-го. Осью zi поступательной пары является какая-либо из прямых, параллельная направляющей данной поступательной пары. Если ось zi не параллельна оси zi-1, то ее рекомендуется направлять так, чтобы она пересекалась с этой осью. За положительное направление оси zi можно взять любое, в частности, направление снизу вверх, слева направо, в направление к наблюдателю или близкие к ним направления. Важным моментом при расположении системы координат на i-м звене манипулятора является выбор ее начала координат Оi и направление оси xi. Введем соответствующие правила для различных случаев взаиморасположения осей zi и zi-1. Оси zi и zi-1 перекрещиваются (рис. 6.8): начало координат располагается в точке пересечения линии кратчайшего расстояния между осями zi и zi-1 с осью zi. В этом случае ось хi направляется по линии кратчайшего расстояния в сторону от оси zi-1 к оси zi.
Оси zi и zi-1 параллельны (рис. 6.9): за начало координат может быть принята любая удобная по каким-либо соображениям точка оси zi. Ось хi направляется так, чтобы она лежала в плоскости, образуемой осями zi и zi-1. (Случай рассматривается как частный по отношению к предыдущему.). Оси zi и zi-1 совпадают (рис. 6.10): начало Оi системы координат может быть назначено в любой удобной по каким-либо дополнительным условиям точке оси zi, а ось хi направлена перпендикулярно оси zi в произвольном направлении (как правило, в направлении развития i-го звена, т. е. по i-му звену).
Оси zi и zi-1 пересекаются (рис. 6.11): за начало Оi координат принимается точка их пересечения, а ось хi направляется по общему перпендикуляру к осям zi и zi-1. Ось уi направляется так, чтобы система координат была правой.
Эти правила не действуют в полной мере при выборе системы координат, связанной со стойкой (звено 0), так как отсутствует (i-1)-я кинематическая пара, и системы координат, связанной с последним звеном, на котором закрепляется схват, так как это последнее звено не содержит кинематической пары для соединения со следующим звеном. Начало О0 системы координат, связанной со стойкой, может быть расположено в любой точке оси z0, а направление оси x0 принимается произвольно по дополнительным условиям (рис. 6.12).
Начало Оn системы координат, связанной с последним n-м звеном манипулятора (рис. 6.13), на котором закреплен схват, располагается в точке, принимаемой за центр схвата, а ось хn направляется перпендикулярно оси zn-1. Оси zn может быть назначено произвольное направление, например по оси захватываемой детали или технологического инструмента или перпендикулярно ей.
6.4. Однородные координаты. При составлении математических моделей манипуляторов наибольшее распространение получило матричное исчисление (матричное исчисление было предложено в 1857 г. английским ученым Кэли). Долгое время для этой цели использовалось сочетание матриц поворота размером 3×3, элементами которых были направляющие косинусы углов между осями (трех осей одной системы координат относительно трех осей другой), и матриц переноса размером 3×1, элементами которых служили координаты по трем осям начала соответствующей системы координат. Наличие двух матриц разной размерности и разного назначения привело к необходимости использовать операции умножения и сложения матриц, к усложнению алгоритма вычисления, а следовательно, к увеличению машинного времени, что сказывается на отработке управляющих сигналов в реальном времени и на управляемости робота. В последние десятилетия стали использовать комплексные матрицы перехода размером 4×4, позволяющие осуществлять поворот и перенос (смещение) одних координат по отношению к другим. В этом случае для описания положения точки в пространстве используются однородные координаты, в которых к обычным координатам добавляется четвертая, равная единице, то есть координатами точки будут (xi, yi zi, 1). Если известны однородные координаты (xi, yi, zi, 1) вектора r i некоторой точки Ai в «старой» i-й системе координат, то однородные координаты (xi-1, yi-1, zi-1, 1) вектора r i-1 этой точки Ai в «новой» (i-1)-й системе координат рассчитываются в общем случае по формулам:
где C – символ, обозначающий тригонометрическую функцию «cosines»;
Взаиморасположение i-й системы координат относительно (i-1)-й представлено на рисунке 6.14: на рисунке 6.14а показаны координаты хi-1, у i-1, z i-1 и хi-1, у i-1, z i-1, а на рисунке 6.14б, углы а) б) Рис. 6.14. Взаиморасположение i-й и (i-1)-й систем координат
Выражение (6.1) можно переписать в матричном виде:
однородная матрица перехода от системы i к (i-1)-й системе координат. Матрицу
является матрицей поворота i-й системы координат относительно (i-1)-й и содержит соответствующие направляющие косинусы. Матрица
Переход от одной системы координат к другой с помощью матричного аппарата оказывается удобным средством описания кинематики манипулятора. Чтобы использовать матричный аппарат преобразования координат для описания кинематики манипуляторов, свяжем по изложенным ранее правилам с каждым i-м звеном манипулятора специальные системы координат, расположенные определенным образом в i-й кинематической паре. В этом случае переход от i-й системы координат к (i-1)-й с помощью однородной матрицы перехода При переходе от i-й системы координат к (i-1)-й полагают, что оси i-й системы, «уходя» от (i-1)-й, из положения, когда они полностью совпадали с Иногда удобно считать, что до совмещения с i-й системой должна перемещаться (i-1)-я система координат до полного совпадения с i-й системой, как бы повторяя перемещения, которые произвела i-я система, «уходя» от (i-1)-й. В общем случае, чтобы совместить «новое» (i-1)-е положение со «старым» i-м положением системы, используя движение «новой» системы к «старой», необходимо шесть независимых перемещений относительно трех осей координат. Однако при использовании специальных систем координат и так называемых преобразований Денавита-Хартенберга достаточно четырех перемещений, осуществленных в следующей последовательности (рис. 6.15):
1. Поворот системы (i-1) вокруг оси Zi-1 против часовой стрелки (если смотреть со стороны оси Zi-1) на угол 2. Сдвиг повернутой (i-1)-й системы вдоль оси Zi-1 на величину Si до совмещения оси Xi-1 с осью Xi. 3. Сдвиг системы (i-1) вдоль оси Xi на величину ai до совпадения начал координат систем (i-1) и i. 4. Поворот (i-1)-й системы вокруг оси Xi против часовой стрелки (если смотреть со стороны оси Xi) на угол Покажем перечисленные эволюции (i-1)-й системы координат применительно к звеньям манипулятора (рис. 6.15).
Рис. 6.15. Преобразования Денавита – Хартенберга
Каждое из упомянутых элементарных движений (i-1)-й системы координат описывается соответствующей частной матрицей перехода: 1. Поворот системы (i-1) вокруг оси Zi-1 на угол
2. Сдвиг по оси Zi-1 на величину Si:
3. Сдвиг по оси Xi на величину ai:
4. Поворот вокруг оси Xi на угол
где S есть тригонометрическая функция «sinus». Результирующая матрица перехода от i-й системы координат к (i-1)-й, то есть матрица, осуществляющая преобразования системы координат i-го звена в систему координат (i-1)-го звена, получается путем перемножения частных матриц перехода:
После преобразования результирующая матрица принимает вид:
Заметим, что параметры Θi, S i,, α i,, α i могут принимать и отрицательные значения.
По рисунку 6.15 можно убедиться в достоверности формул для расчета координат
6.5. Определение ориентации звеньев манипуляторов Кроме направляющих косинусов, т. е. углов между осями координат Xi-1, Zi, Yi-1, Zi и Xi-1, Yi при определении ориентации звеньев манипулятора успешно используются углы Эйлера. Существует три системы углов Эйлера (Euler). В кинематике роботов используется система углов Эйлера, которая применяется в теории гироскопов и в астрономии при описании движения космических тел (рис. 6.16а): 1) поворот на угол прецессии YI вокруг оси Zi-1; 2) поворот на угол нутации Qi вокруг повернутой оси OiXi; 3) поворот на угол собственного вращения ji вокруг повернутой оси OiZi. Угол прецессии – угол ометания, движения впереди, преддвижения. Угол нутации – угол колебания оси собственного вращения. Угол собственного вращения – угол вращения вокруг собственной оси. Например, при вращении юлы угол Qi с уменьшением угловой скорости
Рис. 6.16. Углы Эйлера
Перечисленные эволюции i-й системы координат отражаются следующим произведением матриц:
Для определения углов Эйлера можно использовать ранее изложенный алгоритм решения прямой задачи кинематики с той разницей, что на заключительном этапе должны быть вычислены значения углов Эйлера из сопоставления соответствующих элементов матриц Тi-1,i и Еi-1,, а именно: 1. Рассчитываем матрицу Тi-1,i, в результате становятся известными численные значения ее элементов.
2. Cопоставим те элементы матриц Тi-1,i и Еi-1,i, которые наиболее просто позволяют определить углы Эйлера, а именно:
Глава 7. Прямая задача кинематики манипуляторов роботов. Абсолютные скорости и ускорения в манипуляционных системах 7.1. Теоретические вопросы решения прямой задачи В принятых нами специальных системах координат ось Zi всегда направлена: - во вращательной кинематической паре по оси вращения; - в поступательной паре параллельно направляющей кинематической паре. Напомним также, что положение i-го звена относительно (i-1)-го определяется обобщенной координатой qi. Если два звена соединены вращательной парой (рис 7.1а), то при вращении i-го звена относительно (i-1)-го из четырех параметров qi = Если два звена соединены поступательной парой (рис. 7.1б), то при перемещении i-го звена относительно (i-1)-го из четырех параметров q Таким образом, из четырех параметров, ориентирующих i-ю систему координат, а следовательно, и i-е звено относительно (i-1)-го при движении i-го звена относительно (i-1)-го переменным будет один параметр
а) б) Рис. 7.1
Для описания кинематики манипулятора целесообразно использовать специальную таблицу кинематических пар, в которой для конкретного манипулятора проставляются определенные значения параметров
Таблица кинематических пар манипулятора
Рассмотрим пример манипулятора, образованного последовательностью кинематических пар: вращательная – поступательная – вращательная (рис. 7.2).
Рис. 7.2. Специальные системы координат звеньев манипулятора
Обоснуем выбор систем координат звеньев манипулятора. Система О0X0Y0Z0 выбрана произвольно при обеспечении направления оси Z0 по оси кинематической пары А0. В системе О1X1Y1Z1: ось Z1 направлена по направляющей кинематической пары А1 и совмещена с осью Z0. Начало координат О1 может быть выбрано в любой точке оси Z1 – в нашем случае она совмещена с точкой О0. Поэтому Система координат О2X2Y2Z2 выбрана по ранее изложенному правилу: так как пара Система О3X3Y3Z3 выбрана по правилу для действующего n-го (последнего) звена: начало О3 координат назначено в центре А3 схвата, ось Х3 направлена перпендикулярно оси Z2. Так как пара А2 вращательная, то переменным параметром будет угол Примечание: Заполним таблицу кинематических пар для данного манипулятора.
Прямая задача кинематики манипуляторов заключается, как отмечалось, в определении положения его звеньев в неподвижной (инерциальной) системе координат по известным значениям обобщенных координат и при известных значениях кинематических размеров звеньев. Важным частным видом прямой задачи кинематики манипулятора является определение положения его схвата, закрепленного на последнем n-м звене манипулятора. Положение схвата в неподвижной системе координат будет определено полностью, если будут известны координаты его центра Аn и ориентация последнего n-го звена в неподвижной системе координат. В нашем случае, когда в центр Аn схвата помещено начало n-й системы координат, для определения положения и ориентации схвата достаточно определить координаты начала n-й системы координат в системе координат, связанной с 0-м звеном. Запишем формулу (6.2) для n звеньев, как бы «пятясь» от звена n к звену 0.
Подставив в последнее равенство последовательно все предыдущие, получим
или в более общем виде где Каждый элемент матрицы Т0n содержит информацию о взаиморасположении систем координат ОnXnYnZn и О0X0Y0Z0:
Обратим внимание на важное обстоятельство: начало координат n-го звена совпадает с центром схвата. Отсюда вытекает следующее следствие:
Таким образом, первые три элемента 4-го столбца матрицы T0n, а именно элементы В нашем же случае начало координат n-й системы и центр схвата, как отмечалось, совпадают, что и подтверждают равенства: х = Матрица T0n по структуре полностью аналогична любой матрице Тi-1,i (6.7). Значит, как и в матрице Тi-1,i, 1-й элемент 2-го столбца и первые два элемента 3-го столбца будут являться
Теперь можно определить углы между соответствующими осями:
Именно эти углы применительно к звеньям i-1 и i показаны на рисунке 6.14б. Перепишем матрицу T0n, опустив верхние индексы
Заметим, что положение схвата в пространстве (координаты его центра Аn и ориентацию n-го звена) мы определяем шестью наддиагональными элементами матрицы T0n. Таким образом, шесть наддиагональных элементов матрицы T0n дают полную информацию о положении схвата в пространстве. Следовательно, отпадает необходимость в использовании формулы (7.1), а достаточно использовать выражение (7.3) в виде
и воспользоваться наддиагональными элементами а12, а13, а23 и а14, а24,а34. Для определения положения любого промежуточного
Наддиагональные элементы дадут искомое решение. Можно также определить положение любого k-го звена относительно m-го звена (k
Заметим, что в силу закона ассоциативности исходные матрицы – сомножители, записанные в порядке возрастания номеров звеньев и пар манипулятора, можно перемножать как справа налево, так и слева направо. Перемножение справа налево, видимо, более наглядно, т. к. последовательно координаты схвата пересчитываются в предыдущие системы координат: «счет пятясь». Так удобно умножать, когда определяется положение только схвата. Перемножение слева направо позволяет попутно определить положения всех промежуточных звеньев. Для этого достаточно лишь обеспечить в ходе вычислительного процесса запоминание наддиагональных элементов матриц, получаемых как промежуточные при расчете.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 2004; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.202 (0.126 с.) |
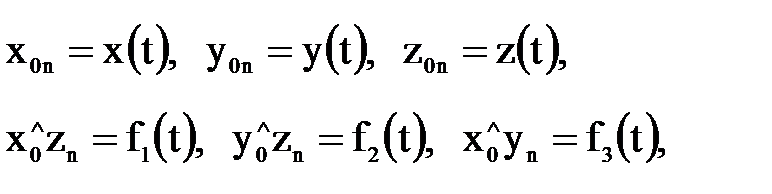
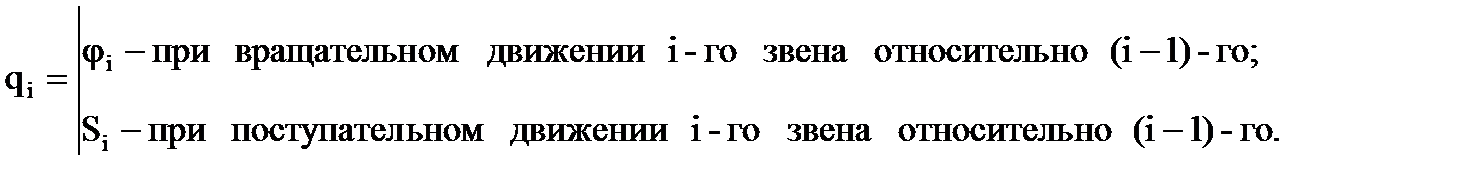
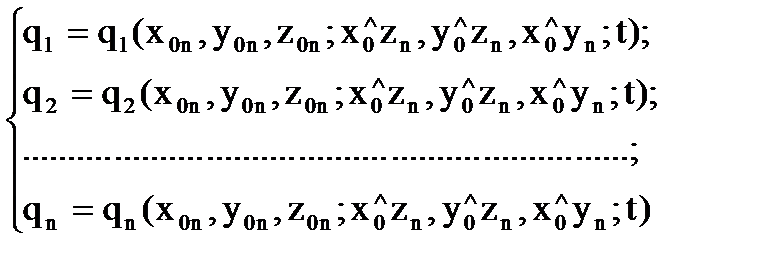
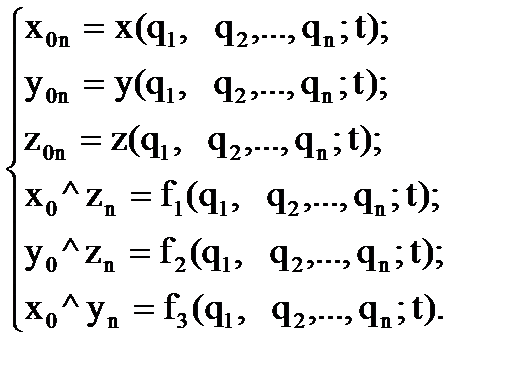
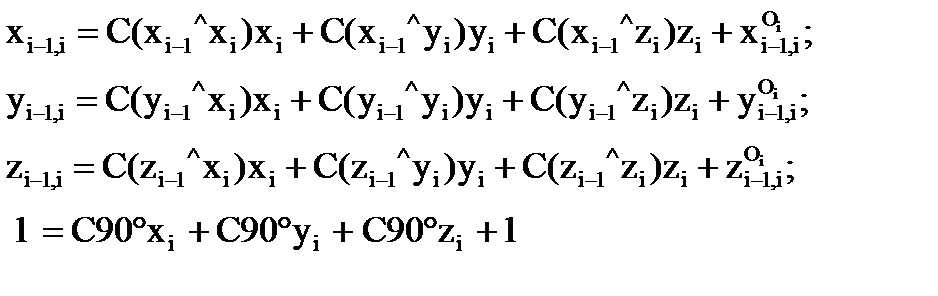
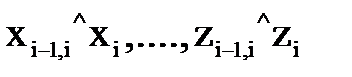 – углы, образуемые осями «старой» i-й системы координат с осями «новой» (i-1)-й системы так, что поворот определенной оси (i-1)-й системы до совмещения с соответствующей осью i-й системы должен видеться против часовой стрелки;
– углы, образуемые осями «старой» i-й системы координат с осями «новой» (i-1)-й системы так, что поворот определенной оси (i-1)-й системы до совмещения с соответствующей осью i-й системы должен видеться против часовой стрелки; 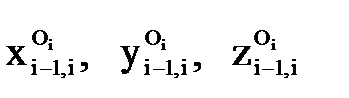 – координаты начала координат Оi i-й системы в системе координат
– координаты начала координат Оi i-й системы в системе координат 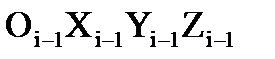 . Тригонометрические функции
. Тригонометрические функции 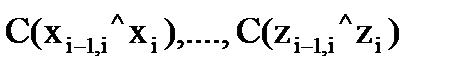 называют направляющими косинусами осей i-й системы в (i-1)-й.
называют направляющими косинусами осей i-й системы в (i-1)-й.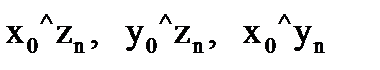 , определяющие ориентацию i-го звена, относительно (i-1)-го.
, определяющие ориентацию i-го звена, относительно (i-1)-го.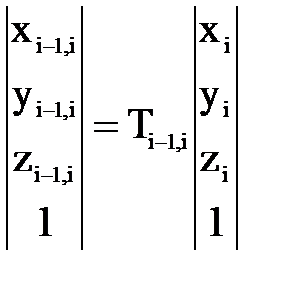
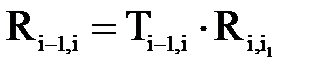 ,
,

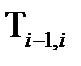 можно представить как блочную матрицу:
можно представить как блочную матрицу: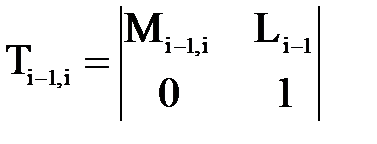
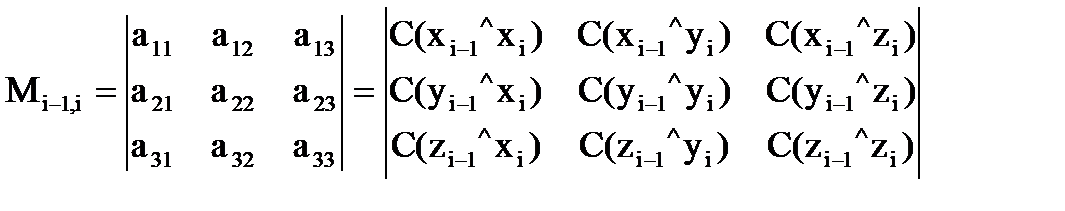
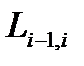 является матрицей переноса начала координат i-й системы до совмещения с началом (i-1)-й системы координат
является матрицей переноса начала координат i-й системы до совмещения с началом (i-1)-й системы координат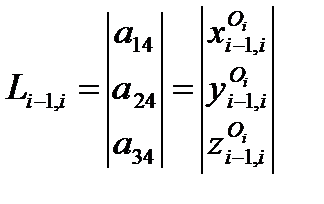 .
.
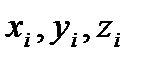 точки А некоторого i-го звена в новую (i-1)-ю систему координат, связанную с (i-1)-м звеном.
точки А некоторого i-го звена в новую (i-1)-ю систему координат, связанную с (i-1)-м звеном.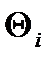 до тех пор, пока ось Xi-1 не станет параллельной и однонаправленной с осью Xi.
до тех пор, пока ось Xi-1 не станет параллельной и однонаправленной с осью Xi.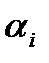 до совмещения оси Zi-1 с осью Zi.
до совмещения оси Zi-1 с осью Zi. ;
;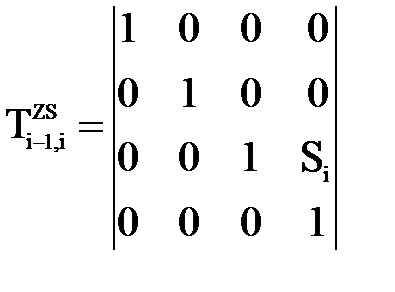 ;
;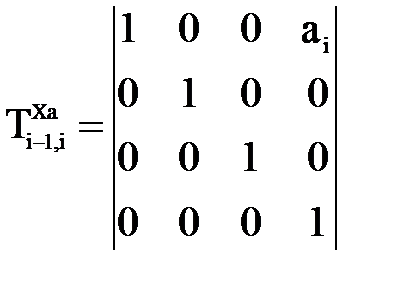 ;
;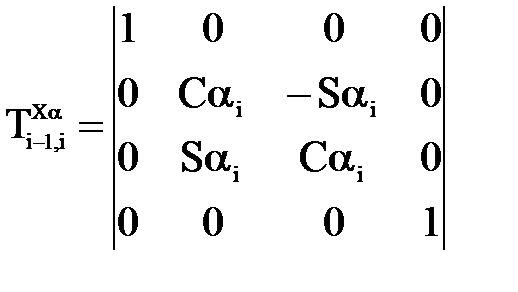
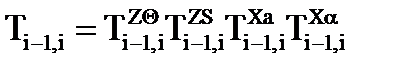 .
.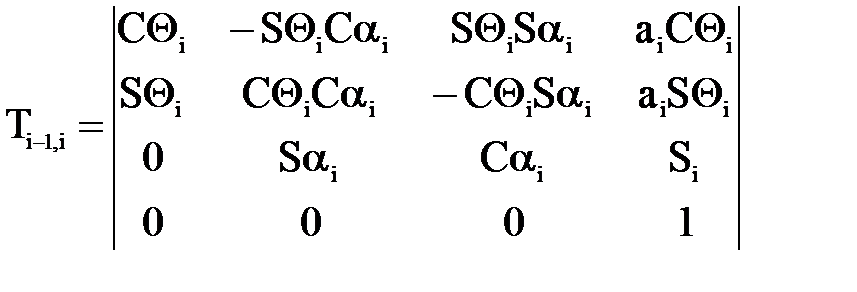
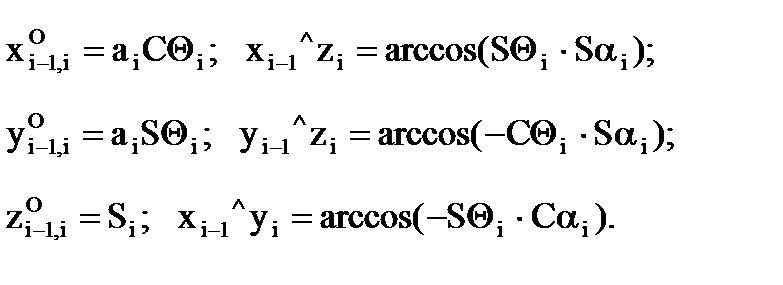
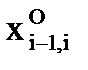 ,
, 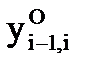 и
и 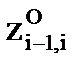 , а также в равенстве углов
, а также в равенстве углов 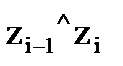 и
и 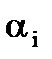 .
.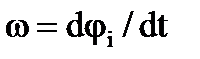 увеличивается и юла падает (рис. 6.16б).
увеличивается и юла падает (рис. 6.16б).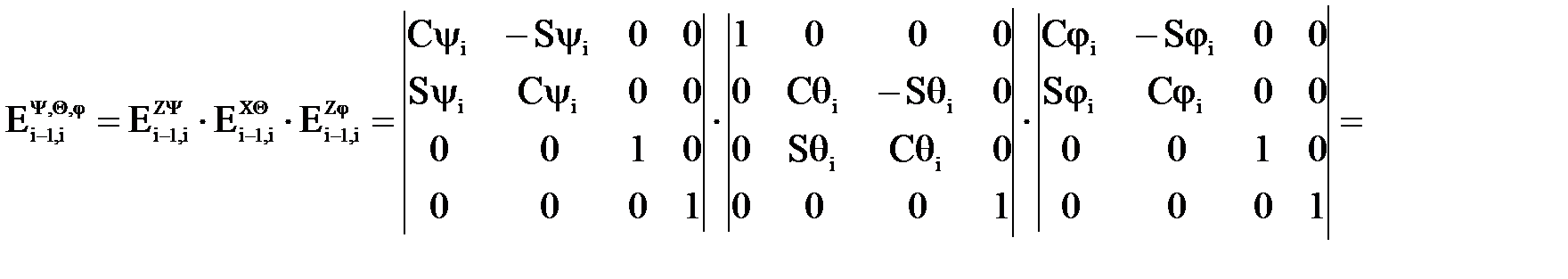
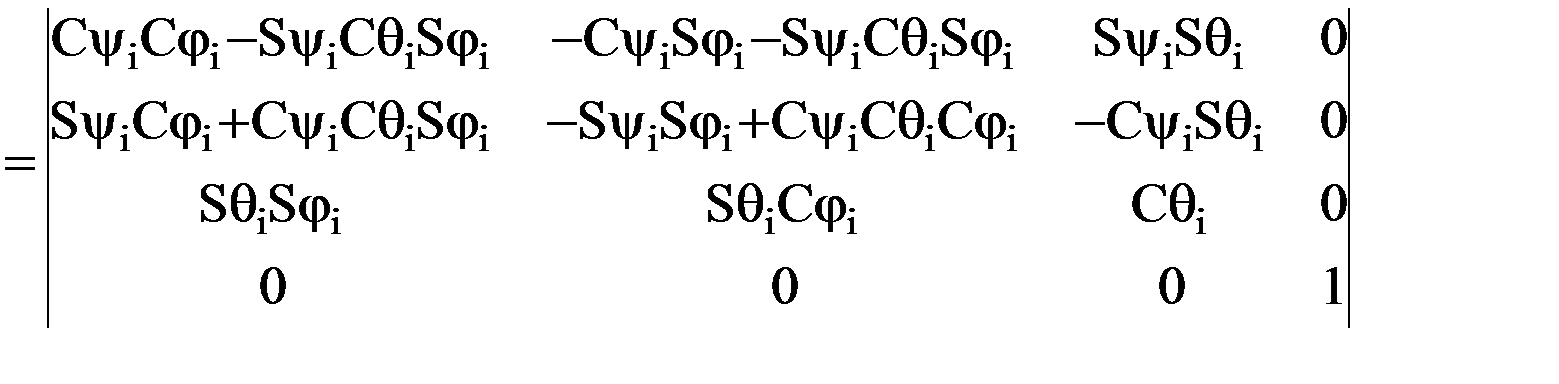
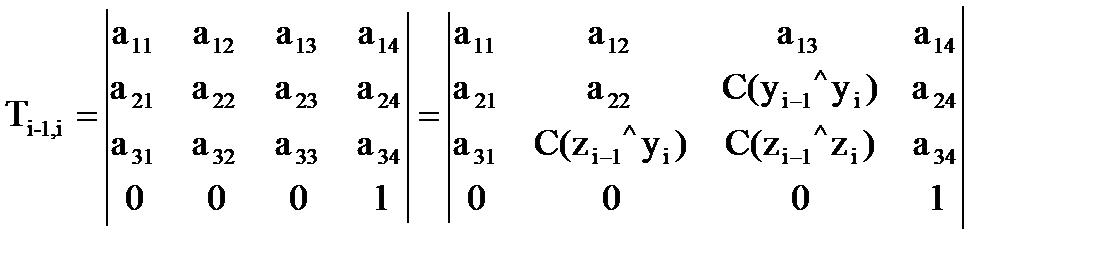
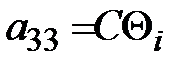 ;
; 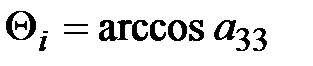 ;
;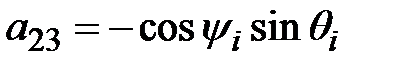 ;
; 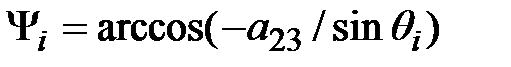 ;
;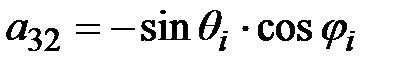 ;
; 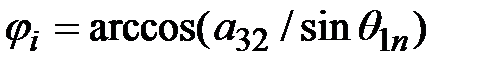 .
. i, Si, ai и ai переменным будет параметр
i, Si, ai и ai переменным будет параметр 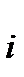 = Si,
= Si, 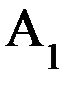 поступательная (звено 2 перемещается относительно звена 1), то расстояние
поступательная (звено 2 перемещается относительно звена 1), то расстояние 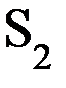 будет переменным, следовательно,
будет переменным, следовательно, 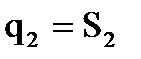 . Величины
. Величины 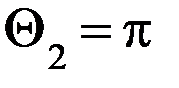 , a
, a 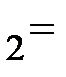 0,5
0,5 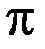 ,
, 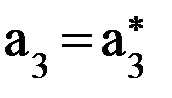 .
.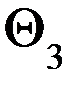 , следовательно,
, следовательно, 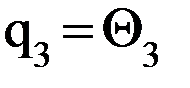 . Параметры S3, a3 и a3 определяются по общему правилу: S3 = 0 (так как после поворота оси Х2 на угол
. Параметры S3, a3 и a3 определяются по общему правилу: S3 = 0 (так как после поворота оси Х2 на угол 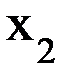 и
и 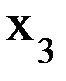 совпали),
совпали), 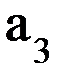 =
= 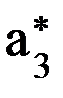 , a3 = - 90o и являются постоянными.
, a3 = - 90o и являются постоянными.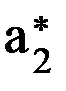 и
и 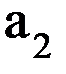 и
и 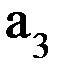 .
. i
i

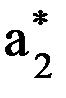
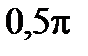
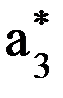
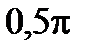
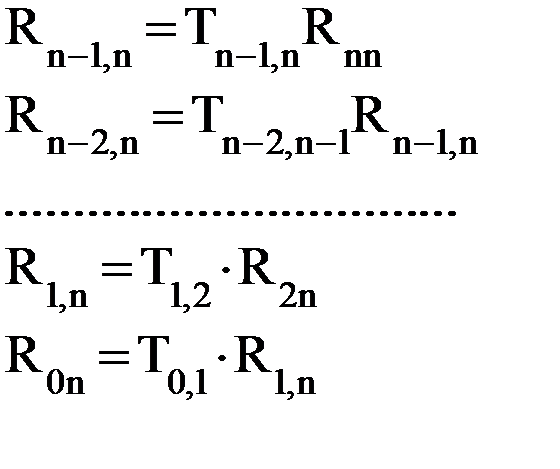
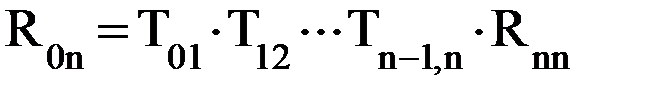
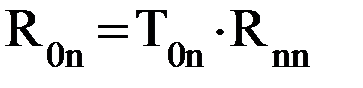 , (7.1)
, (7.1)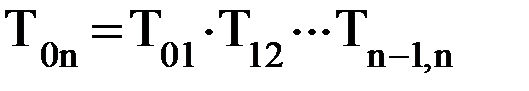 (7.2)
(7.2)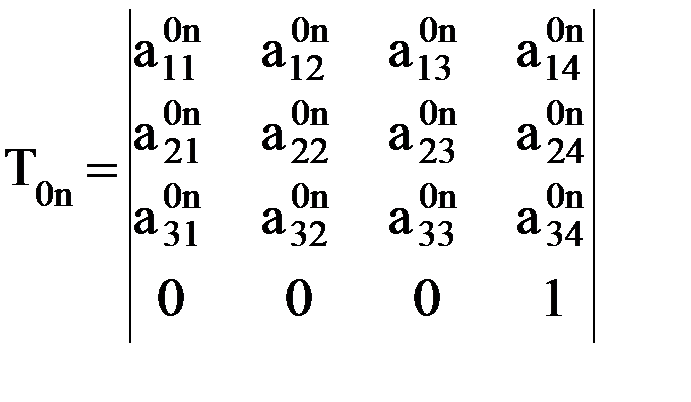
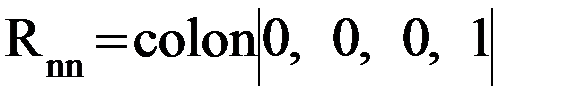 , так как
, так как 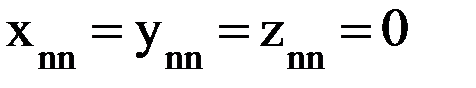 .
.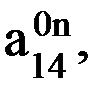
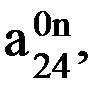
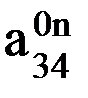 представляют собой координаты центра схвата. Это объяснятся еще и тем, что эти элементы, согласно зависимостям (6.3) – (6.6), являются координатами, которые отражают смещение (перенос) начала координат n-й системы относительно 0-й неподвижной системы координат.
представляют собой координаты центра схвата. Это объяснятся еще и тем, что эти элементы, согласно зависимостям (6.3) – (6.6), являются координатами, которые отражают смещение (перенос) начала координат n-й системы относительно 0-й неподвижной системы координат.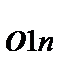 =
=  направляющими косинусами осей zn и yn относительно осей х0 и y0, а именно:
направляющими косинусами осей zn и yn относительно осей х0 и y0, а именно: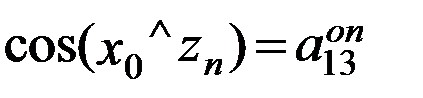 ;
; 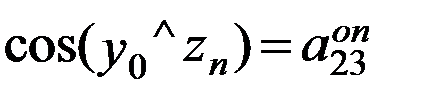 ;
; 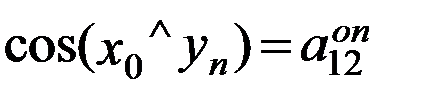 .
.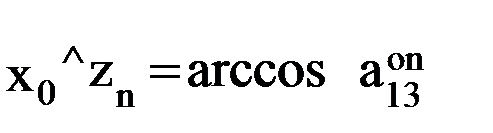 ,
, 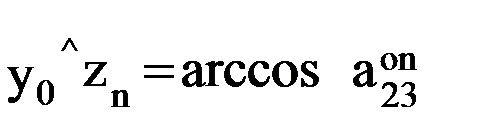 ,
, 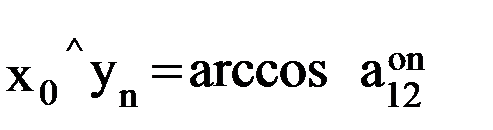 .
.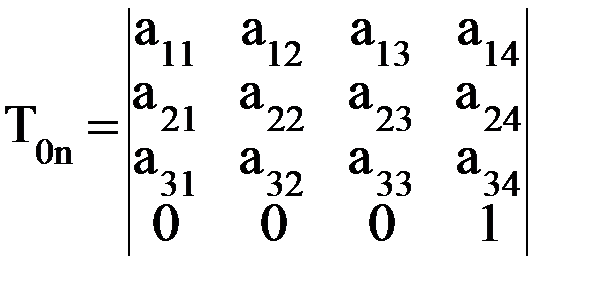 .
.
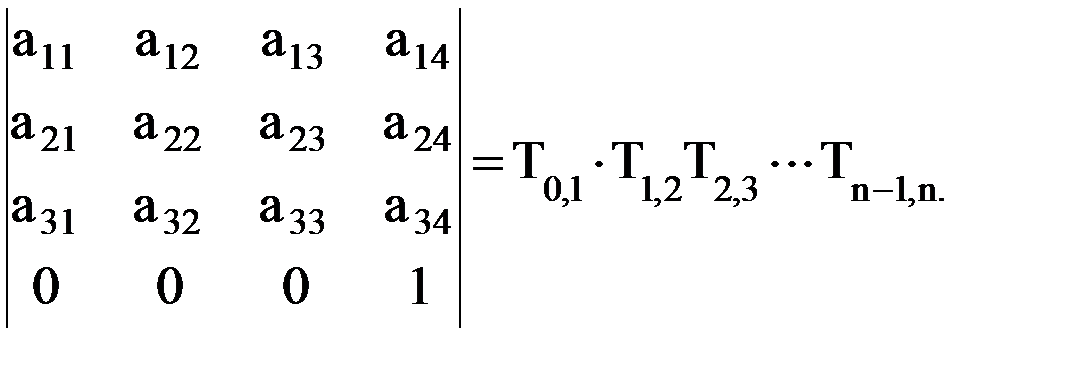
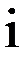 -го звена манипулятора относительно стойки надо перемножить соответствующее число первых слева матриц перехода, то есть воспользоваться выражением
-го звена манипулятора относительно стойки надо перемножить соответствующее число первых слева матриц перехода, то есть воспользоваться выражением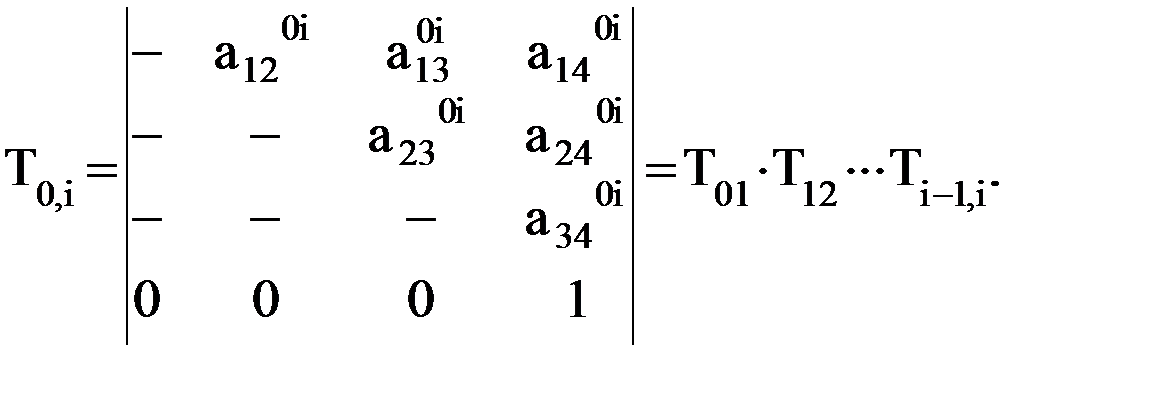
 m) по формуле
m) по формуле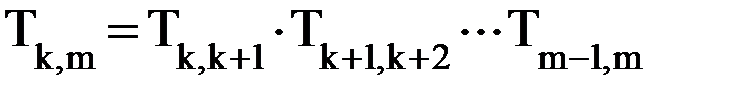 .
.


