
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При позиционном (цикловом) управленииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Позиционное управление обеспечивает движение схвата от одной фиксированной точки к другой с остановкой в каждой точке. Поэтому с теоретической точки зрения достаточно рассмотреть движение между двумя соседними точками, которые можно назвать: одну начальной, в которой схват находится в данное время, другую – конечной, куда схват должен переместиться. При позиционном управлении таких точек обычно более двух: 3,4,…N. Цикловое управление является частным случаем позиционного. При цикловом управлении задаются две точки позиционирования, находящиеся, как правило, на значительном расстоянии друг от друга: место хранения заготовок – рабочая зона станка. На данном этапе будем считать, что для решения прямой задачи при позиционном управлении известны координаты начальной и конечной точек схвата в неподвижной системе координат, связанной с неподвижным (0-м) звеном манипулятора. И главное, будем считать, что известны значения обобщенных координат, соответствующих начальному и конечному положениям схвата. Например, для двухподвижного манипулятора (рис. 7.3) должны быть известны значения:
1-я подзадача: планирование траекторий в пространстве обобщенных координат. Эта подзадача сводится к определению положения одного звена относительно предшествующего ему звена, то есть к определению обобщенных координат в функции времени:
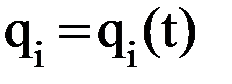 , ( , ( ). ).
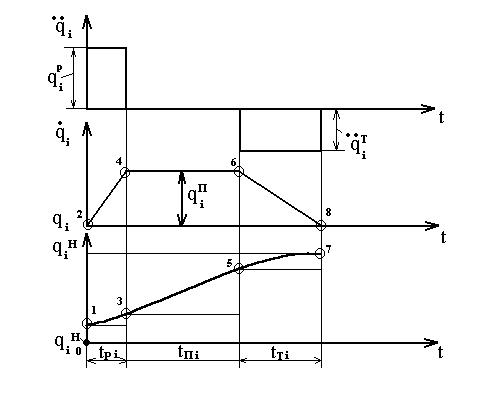
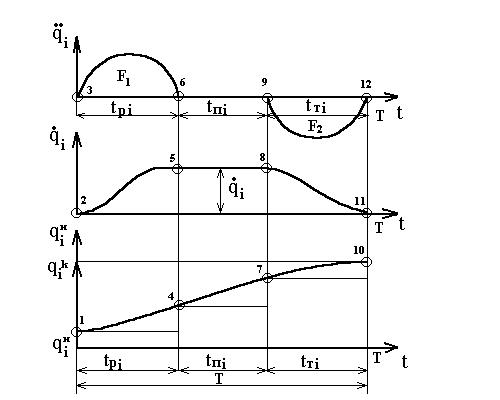
2-я подзадача заключается в определении траектории движения схвата и его ориентации в пространстве (при необходимости и всех других характерных точек звеньев) при его движении от начальной точки к конечной. Решение 1-й подзадачи начинается с выбора общего вида закона движения звеньев по обобщенной координате. Наибольшее распространение получили два закона движения: прямоугольный и синусоидальный законы движения (название дано по виду диаграмм ускорений). Для прямоугольного закона характерно минимально возможные при данной длительности интервалов разгона и торможения значения ускорений, следовательно, и сил инерций при движении одного звена относительно другого. Однако в начале и конце интервалов разгона и торможения возникают так называемые «мягкие» удары, связанные с мгновенным изменением в указанные моменты инерционных воздействий (сил или моментов сил инерций). При движении i-го звена относительно (i-1)-го по прямоугольному закону (рис. 7.4) i-е звено на интервале tр разгоняется под действием прилагаемого усилия, развивающего постоянное ускорение На интервале торможения работают устройства торможения, которые развивают силовое воздействие для обеспечения отрицательного ускорения Длительности интервалов разгона tрi, движения с постоянной скоростью tПi и торможения tTi связаны зависимостью Так как в конце интервала разгона и в начале интервала торможения скорость i-го звена одинакова, то При выбранных длительностях интервалов разгона и торможения необходимо найти такую величину ускорения По графику перемещения i-го звена (рис. 7.4) можно записать уравнение связи:
где Откуда с учетом зависимости (7.5) получим
Рис. 7.4. Закон движения – прямоугольное ускорение
После определения обобщенных ускорений - участок разгона
- участок движения с постоянной обобщенной скоростью
- участок торможения
Итак, получены зависимости Выше получен закон движения исходя из физических представлений. Подойдем к синтезу этого закона чисто формально. Полученный закон движения представляет собой простейший пример использования сплайн-функций для описания относительного движения звеньев по обобщенной координате. Рассмотрим полученную функцию именно как сплайн-функцию, то есть кусочно-непрерывную функцию, составленную из нескольких отрезков некоторых непрерывных функций: график требуемой функции должен пройти через восемь фиксированных точек (рис. 7.4), которые можно использовать в качестве условий проектирования закона движения. Для их удовлетворения надо в аналитическом выражении иметь восемь свободных коэффициентов. Тогда: - для 1-го участка - для 2-го участка - для 3-го участка Сформулируем граничные условия: t = 0; 1)
Подставляя значения обобщенных координат, скоростей и ускорений на границах участков в полиномы, выражающие законы движения, и в их производные, получим после преобразований и решения соответствующей системы уравнений:
Из чисто формальных соображений получены те же самые основные зависимости. Заметим, что по различным степеням подвижности значения интервалов разгона, движения с постоянной скоростью и торможения в общем случае могут быть различны. Для обеспечения более плавной безударной работы привода i-го звена используют законы движения, в которых ускорение плавно изменяется от нуля в начале интервала разгона до некоторой максимальной величины, а затем плавно убывает до нуля. Одним из наиболее распространенных законов такого типа является синусоидальный закон (рис. 7.5).
Рис. 7.5. Синусоидальный закон движения
Для установления зависимостей между длительностями интервалов, величинами обобщенных ускорений, скоростей и перемещений здесь удобно использовать диаграмму обобщенных скоростей
Интегрируя эту зависимость от 0 до Т и приравнивая результат к перемещению по обобщенной координате Дифференцируя выражение для обобщенной скорости Полученные законы движения являются, по сути, сплайн-функциями, то есть функциями, составленными из отрезков нескольких простейших функций, имеющих касание друг с другом того или иного порядка. При необходимости можно самим сконструировать подходящий закон движения. Вторая подзадача решается с использованием зависимости (7.2)–(7.4) с учетом того, что в каждой матрице
Перепишем выражение (7.2) в виде
из которого в соответствии с (7.4) определим значения шести наддиагональных элементов.
Понятно, что каждый из наддиагональных элементов есть также функция обобщенных координат и времени, то есть Таким образом, решение 2-й подзадачи есть решение основной прямой задачи кинематики манипулятора и она решается по изложенному ранее алгоритму при известных, как результат выполнения 1-й подзадачи, зависимостях
7.3. Определение абсолютных скоростей После того как принят закон изменения обобщенных координат qi(t), можно в соответствии с изложенным ранее матричным методом определить положение схвата и любого другого звена манипулятора в пространстве, т. е. определить координаты их характерных точек и ориентацию как функцию времени. Запишем вновь выражение (7.1): Тогда Так как С формальной стороны назначение вектора столбца
(Производная от матрицы равна матрице, все элементы которой есть производные от элементов исходной матрицы). Таким образом, для определения линейных скоростей точек манипулятора и, в частности схвата, достаточно взять производную по времени от соответствующей матрицы перехода и выделить в ней четвертый столбец. Найдем производную матрицы перехода как производную произведения:
Если бы имелись аналитические выражения для каждого элемента результирующей матрицы перехода, то достаточно было бы продифференцировать по времени эти элементы и получить абсолютные скорости по каждой координате X,Y,Z. Однако обычно располагают только матрицами перехода, перемножая которые определяют координаты необходимых точек манипулятора и ориентацию его звеньев. Если разрабатывается система управления для конкретного манипулятора, то возможно в некоторых случаях провести преобразования и перейти к конкретным аналитическим выражениям. Но это должно оцениваться в каждом конкретном случае: либо целесообразно сокращать затраты времени проектировщиков, либо машинное время при управлении роботом. После того как определены скорости по трем координатам, можно определить полную абсолютную скорость требуемых точек звеньев манипулятора, и в частности центра схвата.
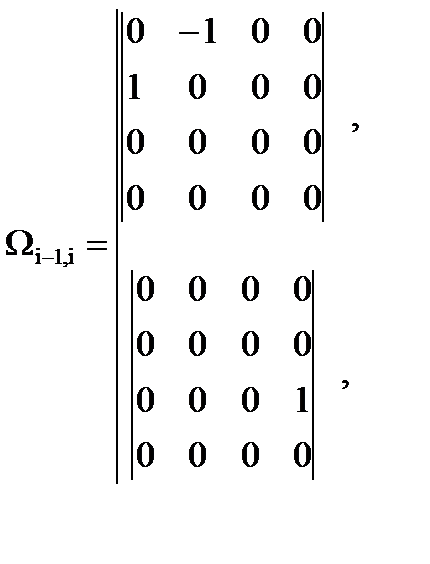
Так как при исследовании кинематики манипуляторов используются специальные системы координат и перемещение i-го звена относительно (i-1)-го всегда происходит по оси Zi-1 либо вокруг нее, то расчет производных от исходных матриц перехода кинематических пар несколько упрощается: чтобы продифференцировать матрицу перехода кинематической пары, достаточно ее умножить слева на матрицу дифференцирования Wi-1,i:
то есть Тогда выражение (7.6) примет вид:
Пример: Пусть матрица перехода будет иметь вид (поворот вокруг оси Zi-1):
Тогда по правилу дифференцирования матриц
С использованием матрицы дифференцирования Wi-1,i:
Определим матрицу - вращательная кинематическая пара
- поступательная кинематическая пара
Зная аналитические выражения матриц скоростей, их можно непосредственно подставлять в выражение (7.6). Смысл использования оператора дифференцирования
Глава 8. Обратная задача кинематики
|
|||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |

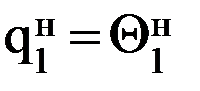 ;
; 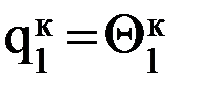 ;
; 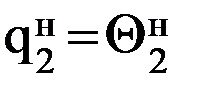 ;
; 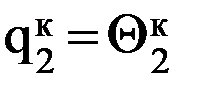 .
.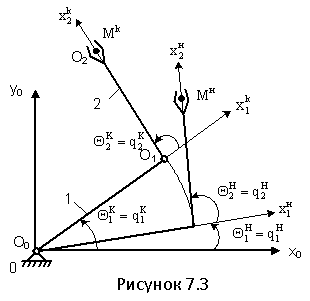 Прямая задача кинематики в этом случае разделяется на две подзадачи:
Прямая задача кинематики в этом случае разделяется на две подзадачи: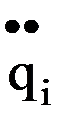 . При достижении скорости
. При достижении скорости 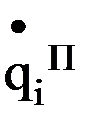 ускорение принимает значение, равное 0, а усилие привода тратится на преодоление сил трения.
ускорение принимает значение, равное 0, а усилие привода тратится на преодоление сил трения.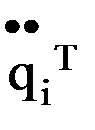 .
.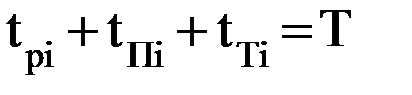 , где Т – заданное время движения от начальной точки к конечной. Поэтому произвольно можно назначать лишь длительности двух интервалов, например: tрi и tTi. Для обеспечения наибольшего быстродействия робота следует принять
, где Т – заданное время движения от начальной точки к конечной. Поэтому произвольно можно назначать лишь длительности двух интервалов, например: tрi и tTi. Для обеспечения наибольшего быстродействия робота следует принять 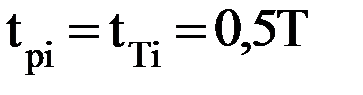 . В этом случае в первую половину интервала движение i-го звена будет равноускоренным, а во вторую – равнозамедленным.
. В этом случае в первую половину интервала движение i-го звена будет равноускоренным, а во вторую – равнозамедленным.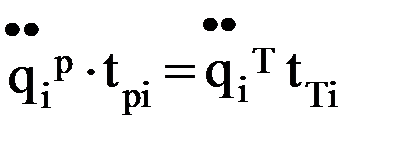 , значит
, значит 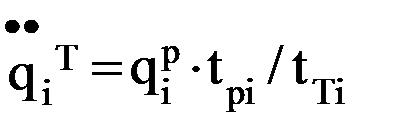 . (7.5)
. (7.5)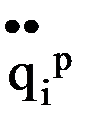 , при которой бы звено за заданное время Т переместилось из начальной точки в конечную.
, при которой бы звено за заданное время Т переместилось из начальной точки в конечную.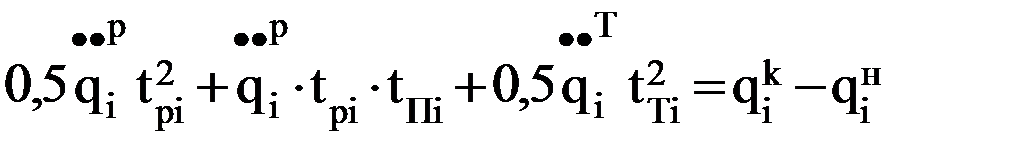 ,
,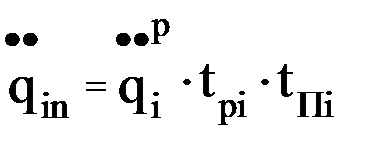 , (i = 1,…,n).
, (i = 1,…,n).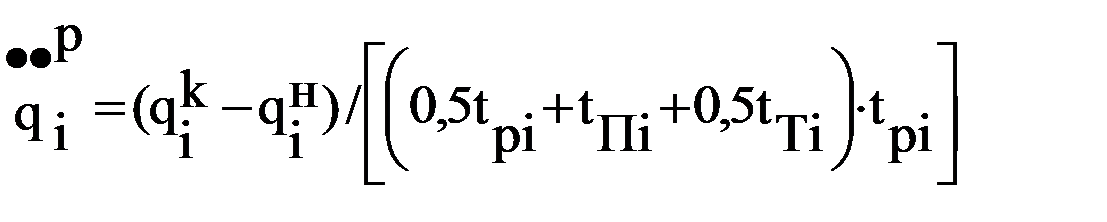 .
.
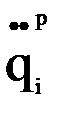 и
и  по известным из физики зависимостям можно определить обобщенные скорости
по известным из физики зависимостям можно определить обобщенные скорости 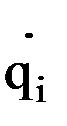 и обобщенные координаты i-го звена в любой момент времени:
и обобщенные координаты i-го звена в любой момент времени: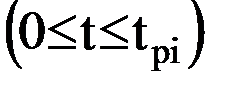
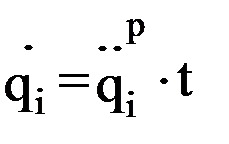 ;
; 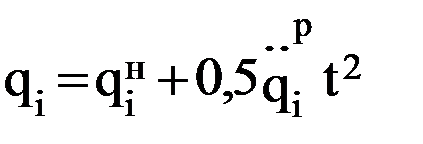 ;
;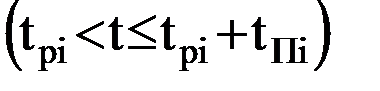
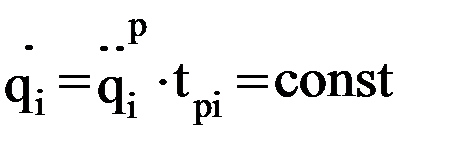 ;
; 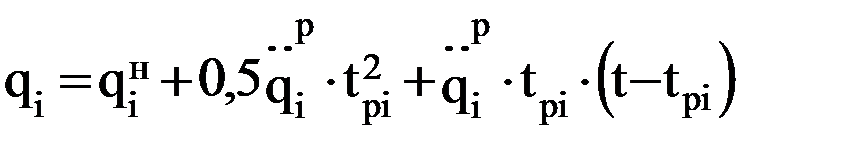 ;
;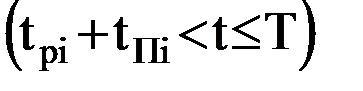 ;
;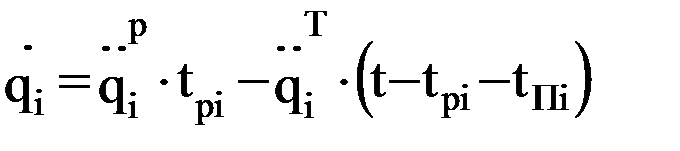 ;
;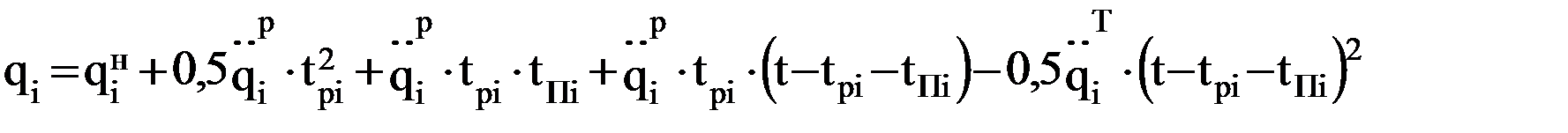 .
.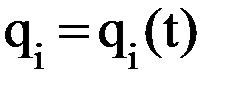 , при
, при 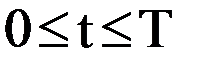 , (i=1,…,n), подставляя которые в формулу (7.4) можно определить траекторию схвата.
, (i=1,…,n), подставляя которые в формулу (7.4) можно определить траекторию схвата.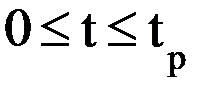
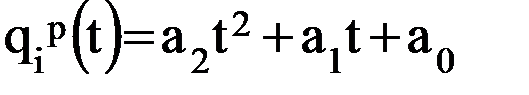 ;
;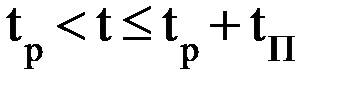
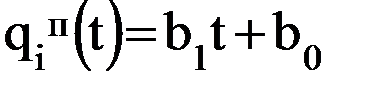 ;
;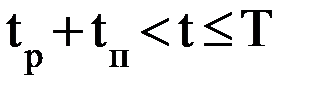
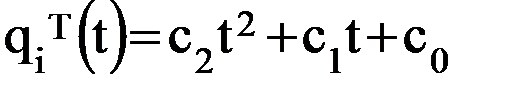 .
.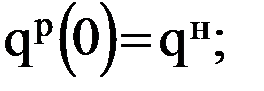 2)
2) 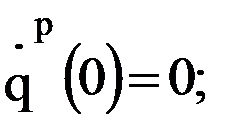
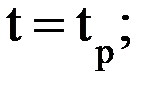 3)
3) 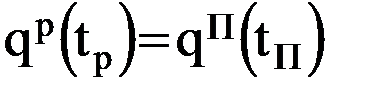 ; 4)
; 4) 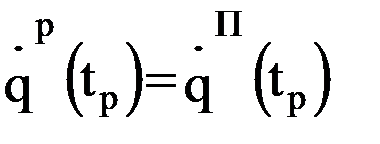 ;
;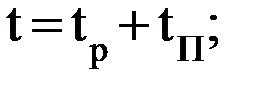 5)
5) 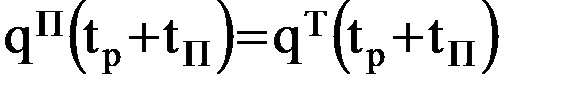 ; 6)
; 6) 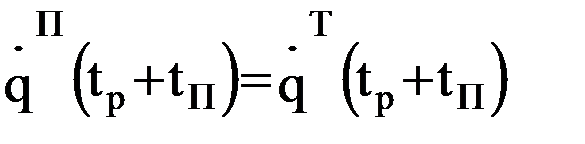 ;
;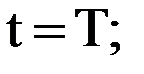 7)
7) 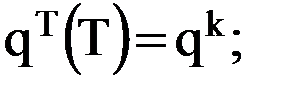 8)
8) 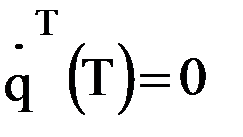 .
.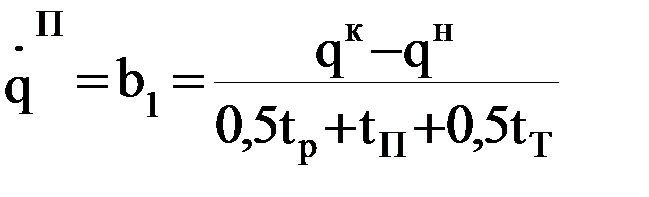 ;
; 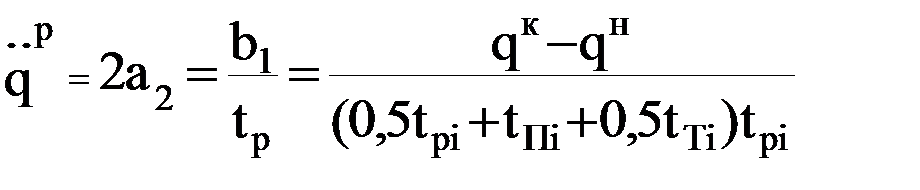 .
.
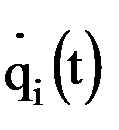 :
: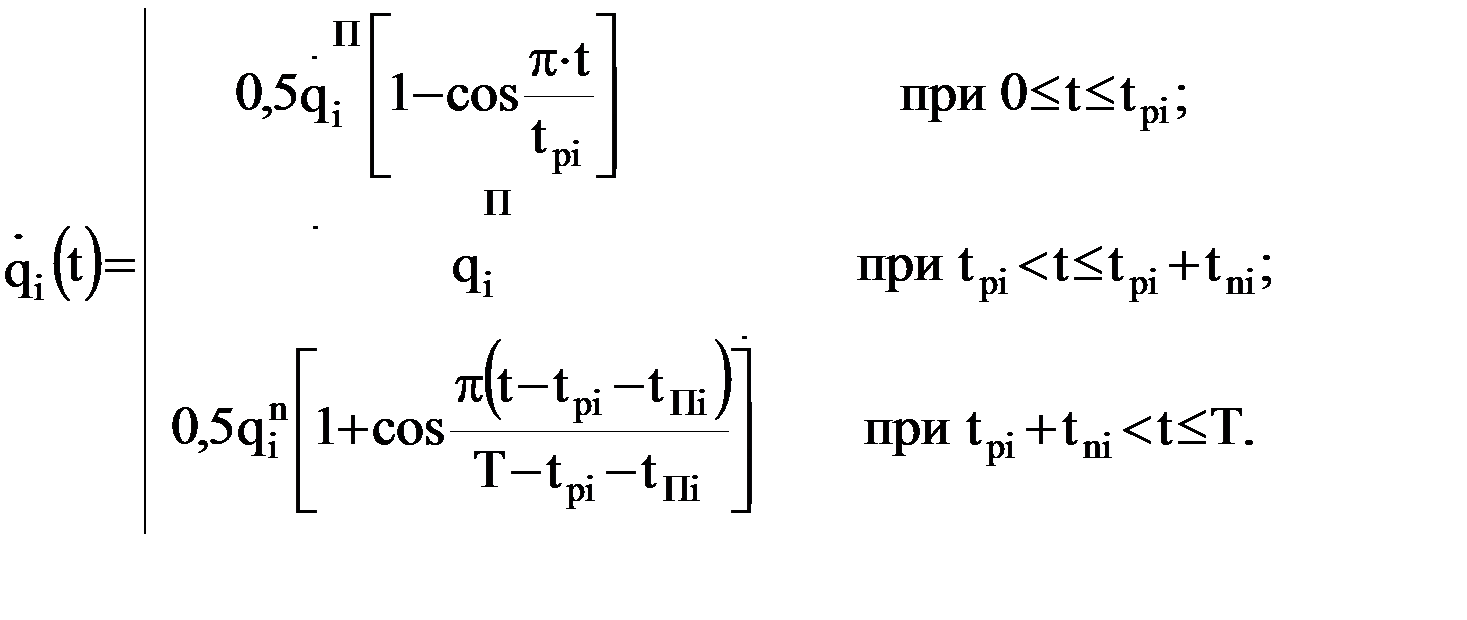
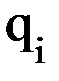 , равному
, равному 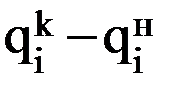 , находится постоянная интегрирования
, находится постоянная интегрирования 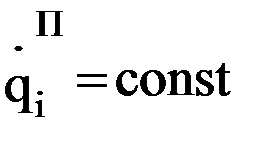 , а после этого и зависимость
, а после этого и зависимость 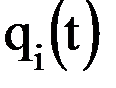 .
.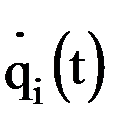 , определим обобщенные ускорения
, определим обобщенные ускорения 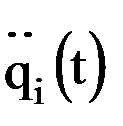 .
.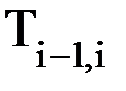 элементы являются функциями одной обобщенной координаты
элементы являются функциями одной обобщенной координаты 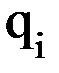 :
: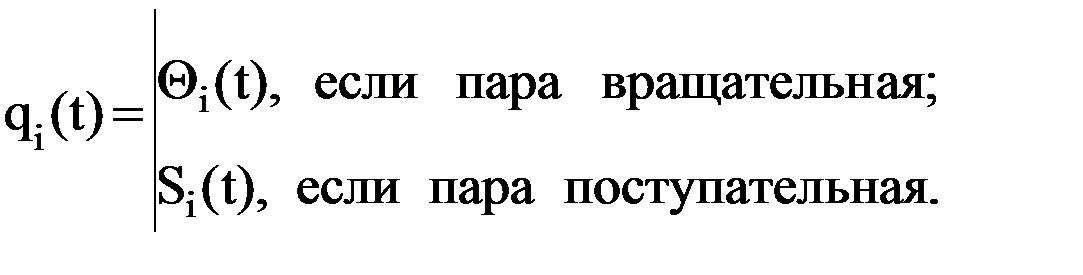
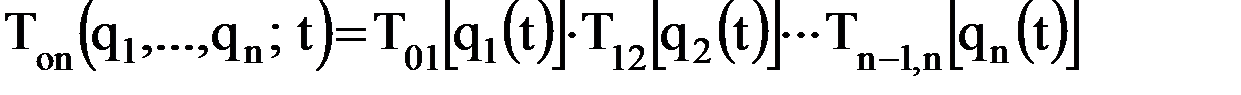

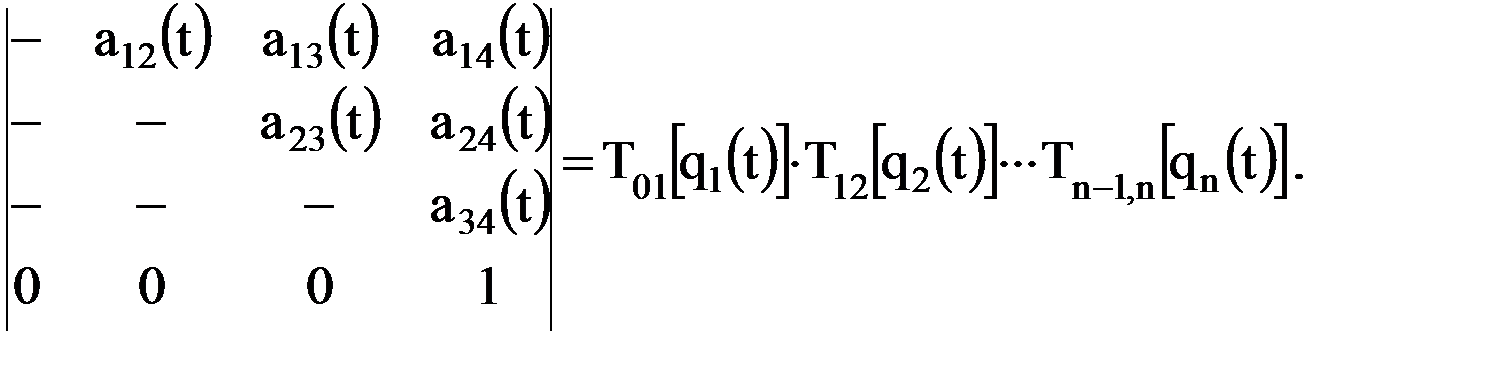
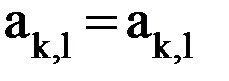 (
(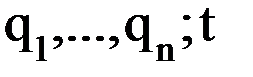 ), (k=1,2,3; l=2,3,4).
), (k=1,2,3; l=2,3,4).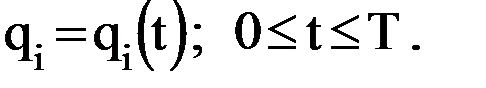
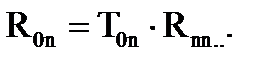
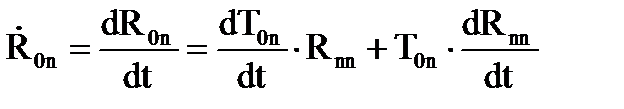 .
.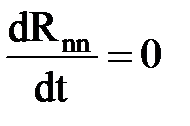 , то
, то 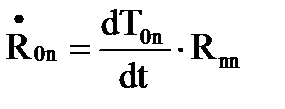 или
или 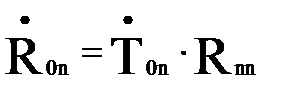
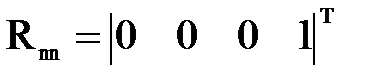 заключается в выделении из матрицы 4x4 подобного ему вектора-столбца, в основе которого будет четвертый столбец матрицы
заключается в выделении из матрицы 4x4 подобного ему вектора-столбца, в основе которого будет четвертый столбец матрицы 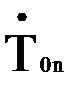 .
.
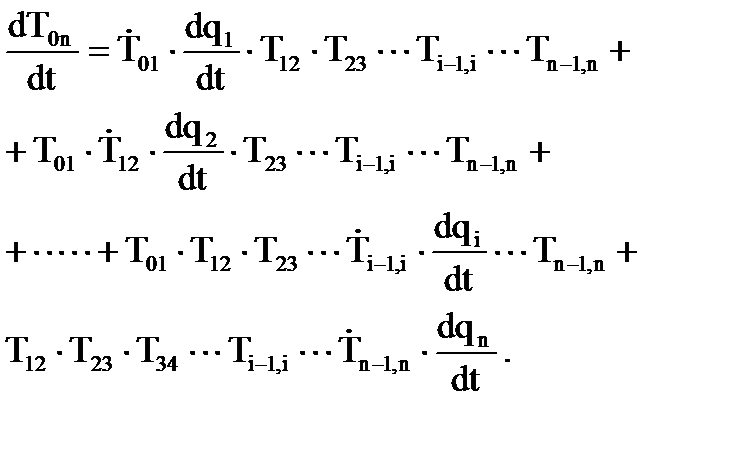 (7.6)
(7.6)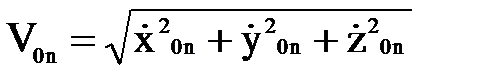 .
.
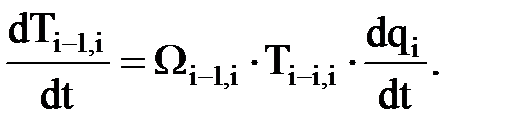
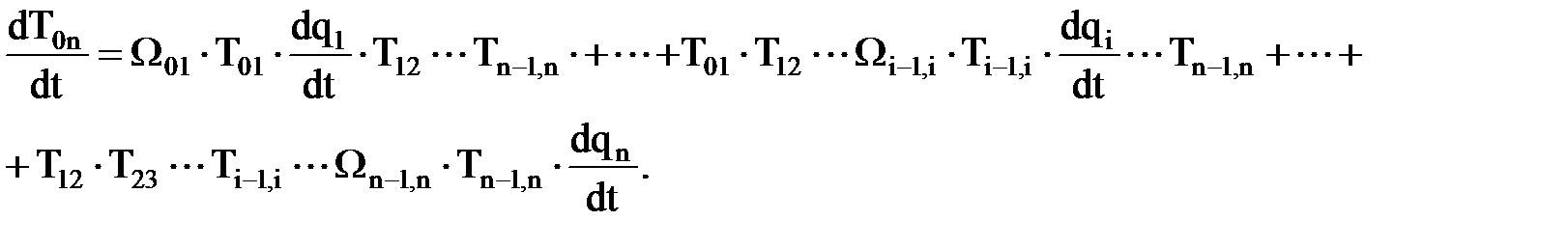

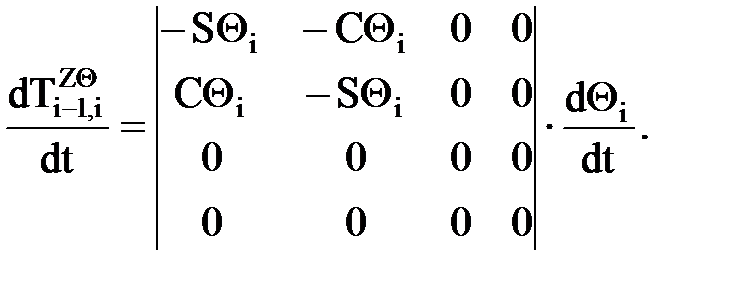
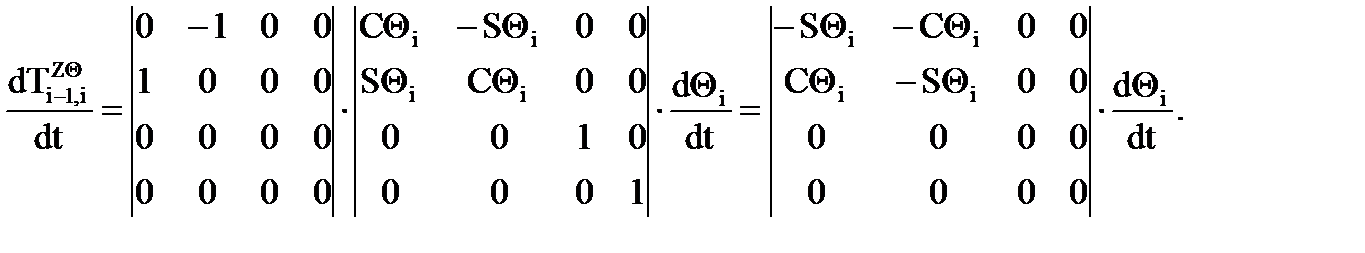
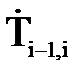 , равную произведению
, равную произведению 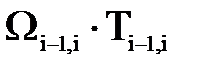 , для вращательной и поступательной кинематических пар:
, для вращательной и поступательной кинематических пар: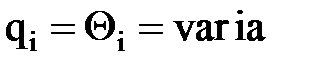 :
: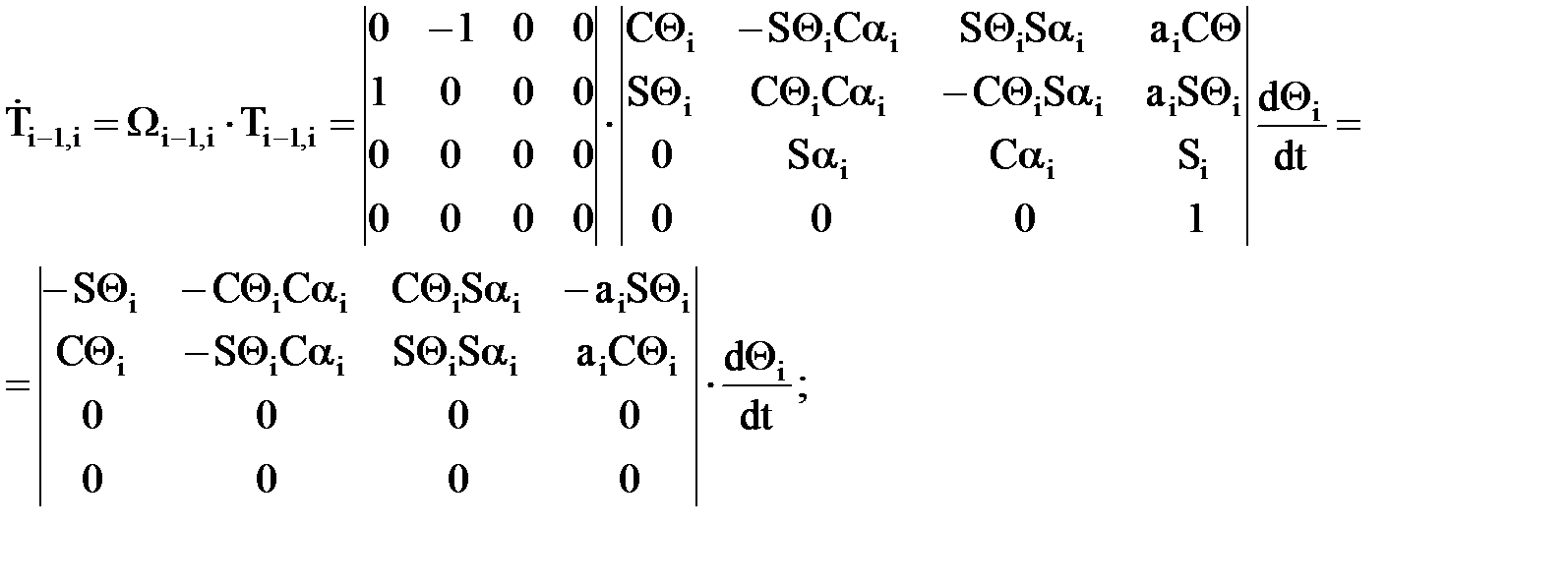
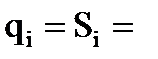 varia:
varia: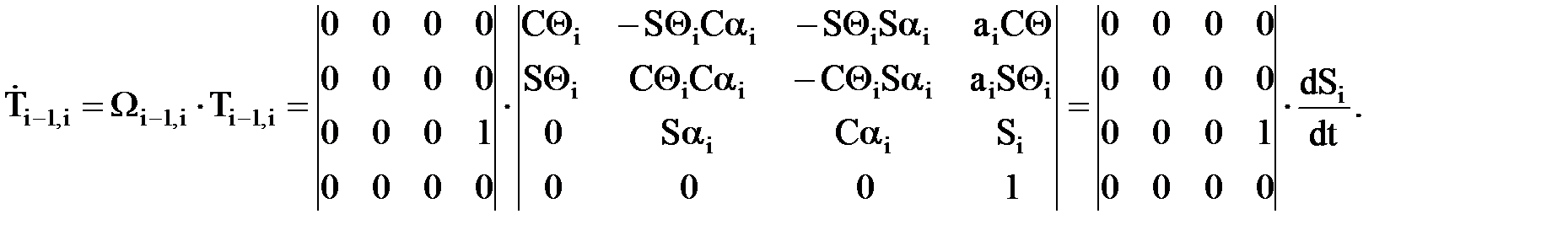
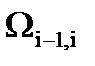 , состоит в сохранении матриц
, состоит в сохранении матриц 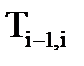 , чтобы не переходить к другим аналитическим выражениям при составлении программ вычисления скоростей.
, чтобы не переходить к другим аналитическим выражениям при составлении программ вычисления скоростей.


