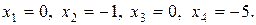Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наближений розв’язок системиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ Мета роботи: Освоїти методику і набути практичні навички розв’язку систем лінійних алгебраїчних рівнянь (СЛАР) методом повного виключення невідомих (методом Жордана – Гаусса). Завдання: 1. Методом Жордана-Гаусса знайти всі загальні і базисні розв’язки системи із чотирьох рівнянь з чотирма невідомими. 2. Розв’язати систему трьох рівнянь з трьома невідомими методом Жордана-Гаусса і з використанням засобу “Поиск решения…” програми Excel. Підготовка до заняття: При підготовці до заняття повторити тему: “Системи лінійних алгебраїчних рівнянь”. Особливу увагу варто звернути на основні визначення: що таке СЛАР; що таке розв’язок СЛАР, що таке спільна СЛАР, спільна визначена, спільна невизначена, неспільна; що таке загальний розв’язок, частковий розв’язок, базисний розв’язок; суть: методу Гаусса і Жордана-Гаусса; формалізації жорданових перетворень. Теоретичні відомості Системою m лінійних алгебраїчних рівнянь з n невідомими називається система вигляду
Розв’язком СЛАР називається сукупність n чисел підстановці цих чисел СЛАР, що не має розв’язків, називається несумісною, що має хоча б один розв’язок – сумісною. СЛАР, що має один розв’язок – сумісно визначеною, що має безліч розв’язків – сумісно невизначеною. Основні задачі, що виникають при розв’язку СЛАР: 1) визначити, сумісна чи несумісна СЛАР; 2) якщо СЛАР сумісна, визначити, чи є вона визначеною; 3) якщо СЛАР сумісна і визначена, знайти її єдиний розв’язок; 4) якщо СЛАР сумісна і невизначена, знайти її загальні і базисні розв’язки. Розглянемо чисельний метод розв’язку СЛАР: метод повного виключення невідомих (метод Жордана–Гаусса). Суть методу полягає у тому, що вибравши r- те рівняння (ведуче), а в ньому невідому xk (ведучу) з коефіцієнтом 1. Всі елементи ведучого рівняння діляться на ведучий елемент 2. Всі елементи ведучого стовпця, крім ведучого, рівні 0; ведучий елемент дорівнює 1; 3. Всі інші елементи перераховуються за правилом прямокутника:
де
Зауваження 1. Якщо в процесі виключення невідомих з'являється рівняння вигляду Зауваження 2. Якщо в процесі виключення невідомих з'являється рівняння вигляду Зауваження 3. У якості ведучих невідомих і ведучих рівнянь вибираються невідомі і рівняння, що раніше не були ведучими. Процес послідовного виключення невідомих закінчується формуванням p ведучих рівнянь:
Система сумісна і тут можливі два випадки: 1. р = n – система сумісна і визначена і має єдиний розв’язок
2. p < n – система сумісна і невизначена. Невідомі х 1, х 2,..., хr,…, xs,…, xp називаються базисними, а xp +1, xp +2,…, xn називаються вільними. Варіанти завдань. 1. Система чотирьох рівнянь з чотирма невідомими. 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29. 31. 33. 35. 37. 39. 41. 43. 45. 47. 49. 2. Система трьох рівнянь з трьома невідомими 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29. 31. 33. 35. 37. 39. 41. 43. 45. 47. 49. Приклад виконання завдання Приклад 1. Знайти всі базисні та загальні розв’язки СЛАР:
Розв’язок. Спочатку знайдемо який-небудь базисний та загальний розв’язок.
Вилучаємо x 1 з усіх рівнянь, крім першого (вводимо в базис x 1).
Вилучаємо х 2 з усіх рівнянь, крім другого (вводимо в базис х 2).
Вилучаємо рівняння 3 та 4
Загальний розв’язок:
Базисний розв’язок
Кількість базисних розв’язків дорівнює базисні розв'язки знаходяться так:
Вводимо в базис х 3 замість х 1
Загальний розв’язок:
Базисний розв’язок:
Вводимо в базис х 1 замість х 2
Загальний розв’язок:
Базисний розв’язок:
Вводимо в базис х 4 замість х 3
Загальний розв’язок:
Базисний розв’язок:
Вводимо в базис х 2 замість х 1
Загальний розв’язок:
Базисний розв’язок:
Вводимо в базис х 3 замість х 2
Загальний розв’язок:
Базисний розв’язок:
Приклад 2. Знайти загальний розв’язок системи рівнянь, використовуючи засіб “Поиск решения... ” програми Excel:
Розв’язок. Для розв’язку системи рівнянь з використанням засобу “Поиск решения...” програми Excel необхідно і достатньо любе із рівнянь системи представити як рівняння функції мети, а інші – як обмеження. Нижче представлений розв’язок, коли перше рівняння виступає як рівняння функції мети.
Рекомендована література: 1. Демидович Б.П., Марон А. Основы вычислительной математики. – М.: Наука, 1966. Стр.268, 272–283. 2. Данилина Н.И. и другие. Численные методы. – М.: Высшая школа, 1976. Стр. 75–85. 3. Кузнецов Ю.Н. Кузубов В. И., Волощенко А. Б. Математическое программирование. –.: Высшая школа, 1980. Стр. 29–36.
Навчально-методичне видання
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 693; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |


 яка при
яка при замість невідомих кожне з рівнянь перетворить у тотожність.
замість невідомих кожне з рівнянь перетворить у тотожність.
 (
(

 – відповідно ведучий і перерахований елементи:
– відповідно ведучий і перерахований елементи:
 СЛАР несумісна.
СЛАР несумісна. то рівняння видаляється із системи.
то рівняння видаляється із системи.

 2.
2. 
 4.
4. 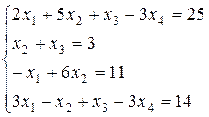
 6.
6. 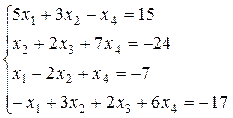
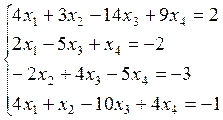 8.
8. 
 10.
10. 
 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 22.
22. 
 24.
24. 
 26.
26. 
 28.
28. 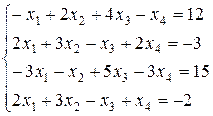
 30.
30. 
 32.
32. 
 34.
34. 
 36.
36. 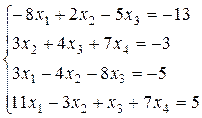
 38.
38. 
 40.
40. 
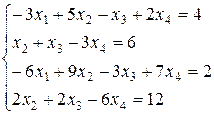 42.
42. 
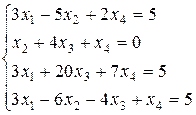 44.
44. 
 46.
46. 
 48.
48. 
 50.
50. 
 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 22.
22. 
 24.
24. 
 28.
28. 



 Інші загальні і
Інші загальні і