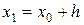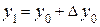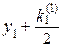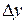Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наближені методи розв’язку звичайнихСодержание книги
Поиск на нашем сайте
ДИФЕРЕНЦІЙНИХ РІВНЯНЬ Мета роботи: Освоїти методику і придбати практичні навички розв’язкузвичайних диференціальних рівнянь першого порядку Завдання: 1. Розв’язати звичайне диференціальне рівняння першого порядку 2. Розв’язати звичайне диференціальне рівняння 1-го порядку 3. Побудувати графіки функцій y = f (x) на відрізку [ а, b ].
Теоретичні відомості Найпростішим звичайним диференціальним рівнянням є рівняння 1-го порядку Для диференціального рівняння n-го порядку
де Для розв’язку поставленої задачі застосовуються наступні методи: Метод Эйлера для розв’язку диференціального рівняння 1-го порядку Вибираємо крок h і складаємо таблицю значень
Метод Рунге-Кутта.
На кожному кроці послідовні значення yi визначають за формулою
Обчислювальна схема методу Рунге-Кутта
Варіанти завдань
Приклад виконання завдання Приклад 1. Методом Эйлера розв’язати звичайне диференціальне рівняння y¢ = y + x, y (0,3) = 0,5 на відрізку [ a, b ], прийнявши крок h = 0,05.
Приклад2. Методом Рунге-Кутта розв’язати звичайне диференціальне рівняння y¢ = y + x, y (0,3) = 0,5 на відрізку [ a, b ], прийнявши крок h = 0,1.
ЛАБОРАТОРНА РОБОТА № 8
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 наближеними методами.
наближеними методами. методом Эйлера на відрізку [ а, b ] із кроком h = 0,1 (
методом Эйлера на відрізку [ а, b ] із кроком h = 0,1 ( ) при початковій умові
) при початковій умові  . Всі обчислення виконувати з чотирма десятковими розрядами.
. Всі обчислення виконувати з чотирма десятковими розрядами. при початковій умові
при початковій умові 
 Загальним розв’язком такого рівняння є безліч функцій
Загальним розв’язком такого рівняння є безліч функцій 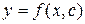 , що відрізняються між собою на довільну постійну с. Якщо задана початкова умова
, що відрізняються між собою на довільну постійну с. Якщо задана початкова умова  то можна виділити частковий розв’язок. Знаходження часткового розв’язку, що задовольняє початковій умові, називається задачею Коші. Іншими словами, задача Коші полягає у відшуканні інтегральної кривої y = y (x), що проходить через задану точку
то можна виділити частковий розв’язок. Знаходження часткового розв’язку, що задовольняє початковій умові, називається задачею Коші. Іншими словами, задача Коші полягає у відшуканні інтегральної кривої y = y (x), що проходить через задану точку 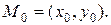
 задача Коші полягає у відшуканні функції
задача Коші полягає у відшуканні функції  яка задовольняє цьому рівнянню і початковим умовам
яка задовольняє цьому рівнянню і початковим умовам
 – задані числа.
– задані числа. з початковою умовою
з початковою умовою 
 , де
, де  ,
,  [ a, b ] – відрізок, на якому шукається розв’язок. Значення
[ a, b ] – відрізок, на якому шукається розв’язок. Значення  визначаються за формулою
визначаються за формулою  .
. , (i = 0,1, 2,…, n),
, (i = 0,1, 2,…, n),