Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод проб (дихотомії, половинного розподілу).
Нехай дано рівняння f (х) = 0, де f (х) неперервна, монотонна функція на відрізку [ a, b ], крім того, f (а)× f (b) < 0. Для уточнення кореня обчислюється значення f (х) у середній точці відрізка [ a; b ] – точці с = (a + b)/2. Якщо f (с) = 0, то с – корінь рівняння. Якщо f (с) Метод Ньютона (метод дотичних). Якщо
Метод ітерацій. Для уточнення кореня методом ітерації рівняння f(x) = 0 еквівалентним чином перетворюється до вигляду x = j(x). Ітераційний процес уточнення кореня сходиться, якщо на інтервалі (а; b) |j¢(x)|<1. Перетворення рівняння f (x) = 0 до вигляду x = j(x): f (x) = 0
Рекурентна формула уточнення коренів:
Варіанти завдань
Приклад виконання завдання Приклад 1. Відділити корені рівняння [-2; 2 ] та уточнити всі корені рівняння методом дихотомії з точністю e = 0,1; e = 0,01; e = 0,001. Розв’язок.
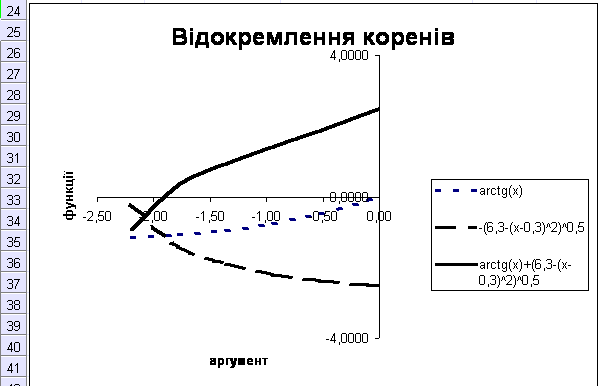
Етап 1. Відділення коренів на відрізку [-2; 2 ]
З графіка видно, що корінь рівняння знаходиться на інтервалі (-2;-1). Перевіряємо правильність відділення кореня.
Корінь відділений правильно. Етап 2. Уточнення коренів. e = 0,1
e = 0,01
e = 0,001
Приклад 2. Уточнити всі корені рівняння e = 0,001 методом ітерацій на відрізку [-2; 2 ]. Розв’язок. Корінь даного рівняння знаходиться на відрізку [-2; -1] Перетворимо рівняння f (x) = 0 до вигляду
с ×( x = x+с ×( j(x) = x+с ×(
j¢(x) = 0,5;
Рекурентна формула:
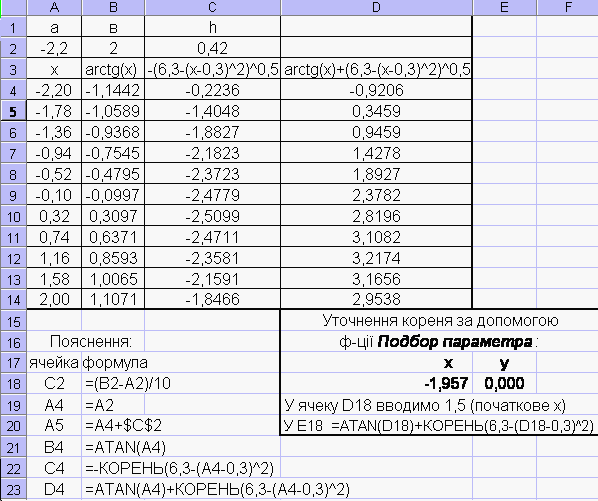
Приклад 3. Розв’язати рівняння Розв’язок. На с. 15 приведений розв’язок за допомогою ф-ції “ Подбор параметра”. Рекомендована література: 1. Демидович Б.П., Марон А. Основы вычислительной математики. – М.: Наука, 1966. Стр. 112–119, 123–131, 135-148. 2. Данилина Н.И. и другие. Численные методы. – М.: Высшая школа, 1976. Стр. 108–123, 127–131, 135–139.
ПРАКТИЧНА РОБОТА № 3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.102.112 (0.018 с.) |
 0, то вибираємо той із проміжків (a, c) чи (c, b), на кінцях якого функція f (x) має протилежні знаки. Процес розподілу проміжку на дві частини проводиться доти, поки не одержимо проміжок (аn, bn), довжина якого не перевищує 2e (e – задана точність обчислення кореня). Корінь рівняння дорівнює
0, то вибираємо той із проміжків (a, c) чи (c, b), на кінцях якого функція f (x) має протилежні знаки. Процес розподілу проміжку на дві частини проводиться доти, поки не одержимо проміжок (аn, bn), довжина якого не перевищує 2e (e – задана точність обчислення кореня). Корінь рівняння дорівнює 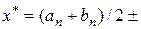 e.
e.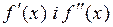 неперервні і зберігають знак на проміжку (a, b), то уточнення кореня виконується за рекурентною формулою
неперервні і зберігають знак на проміжку (a, b), то уточнення кореня виконується за рекурентною формулою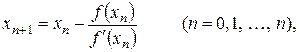
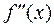 .
.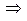 c×f (x) = 0
c×f (x) = 0 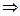 x = x + c×f (x), тобто j(x) = x + c× f (x),
x = x + c×f (x), тобто j(x) = x + c× f (x),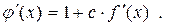 Прирівнюючи j¢(x) 0,5 чи – 0,5, одержуємо
Прирівнюючи j¢(x) 0,5 чи – 0,5, одержуємо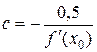 чи
чи  , де
, де 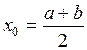 .
.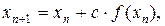 де
де 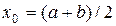 .
. = 0
= 0
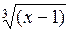 = 0
= 0
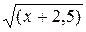 = 0
= 0
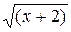 = 0
= 0
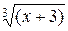 = 0
= 0

 = 0
= 0
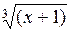 = 0
= 0
 = 0
= 0
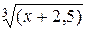 = 0
= 0
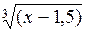 = 0
= 0
 = 0
= 0
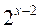 = 0
= 0
 = 0
= 0
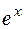 = 0
= 0
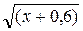 = 0
= 0
 = 0
= 0
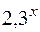 = 0
= 0
 – lg(x + 1) = 0
– lg(x + 1) = 0
 – 1 / lg(x + 2) = 0
– 1 / lg(x + 2) = 0
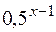 –2 = 0
–2 = 0
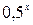 = 0
= 0
 на відрізку
на відрізку

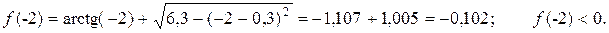
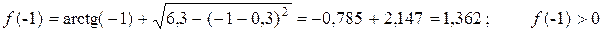


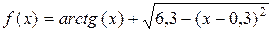
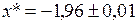
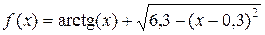
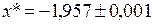
 з точністю
з точністю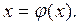
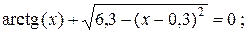


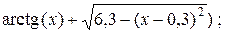
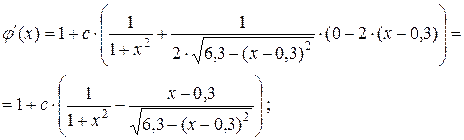
 = 0,5;
= 0,5;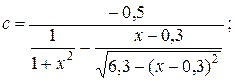
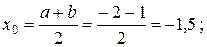
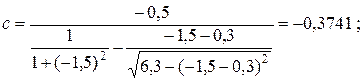
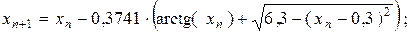


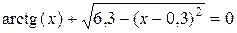 засобами Excel (“Подбор параметра”).
засобами Excel (“Подбор параметра”).