
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заповнення першої симплекс-таблиціСодержание книги
Поиск на нашем сайте Після знаходження ДБР складається перша симплекс-таблиця. 1-ша симплекс-таблиця.
Значенння граф (стовбчикiв) симплекс таблицi: i – номер рядка, x баз – базиснi змiннi в i -му рiвняннi, c баз – коефiцiєнти функцii мети при базисних змiнних в i -тих рівняннях, aij – коефіцієнти при невідомих системи рівнянь (1), B – стовбчик вiльних членiв системи рiвнянь (1). В (m +1)-му рядку записуються значення індексних елементів
де Так,
В (m +1)-му рядку стовбчика В записуються значення функції мети для даного ДБР:
Перевірка отриманого ДБР на оптимальність Критерій оптимальності. При розв’язуванні задачі максимізації план оптимальний, якщо в індексному рядку немає від'ємних елементів, тобто В цьому випадку ДБР При розв’язуванні задачі мінімізації план оптимальний, якщо в індексному рядку немає додатніх елементів, тобто В цьому випадку ДБР В випадках, коли не всі
Перехід до наступної ітерації Для переходу до наступного (кращого) розв'язку необхідно визначити, яку змінну ввести в базис і яку змінну вивести з базису. В базис вводиться змінна з мінімальним від'ємним індексним елеменом Нехай З базису виводиться змінна з мінімальним симплексним відношенням
Нехай Елементи 2-ї симплекс-таблиці визначаються перерахунком 1-ї симплекс таблиці з вирішальним елементом аrk по правилу Жорданових виключень. При цьому в стовбчику x баз в рядку r замість xr записується xk, а в стовбчику c баз замість cr записується ck. Зауваження 1. Якщо є Зауваження 2. 1. При розв'язку задачі мінімізації в базис вводиться змінна xk, яка відповідає максимальному невід'ємному елементу 2. План оптимальний, якщо в рядку Варіанти завдань
1.
3.
5.
7.
9.
11.
13.
15.
17.
19.
21.
23.
25.
27.
29.
31.
33.
35.
37.
39.
41.
43.
45.
47.
49.
Приклад виконання завдання.
z= 3 x 1 + x 2 ® max Розв’язок.
1. Приведемо задану модель до канонічного вигляду. Для перетворення обмежень-нерівностей в рівняння: а) оскільки права частина третього обмеження від’ємна, домножаємо обидві частини рівняння на (–1); б) до лівої частини перших трьох нерівностей додаємо додаткові змінні
z= 3 x 1 + x 2 + 0 х 3 + 0 х 4 + 0 х 5 + 0 х 6 ® max
2. Знайдемо допустимий базисний розв’язок. Оскільки в четвертому обмеженні немає базисних змінних (немає змінних з коефіцієнтом +1, яких немає в інших рівняннях), то до лівої частини додаємо штучну невід’ємну зміну х7.
z= 3 x 1 + x 2 + 0 х 3 + 0 х 4 + 0 х 5 + 0 х 6 – M x 7 ® max
ДБР х 1 = 0, х 2 = 0, х 6 = 0 – вільні змінні, х 3 = 1, х 4 = 7, х 5 = 4, х 7 = 6 – базисні змінні.
3. Заповнення першої симплекс-таблиці.
4. Перевірка отриманого ДБР на оптимальність План х 3 = 1, х 4 =7, х 5 = 4, х 7 = 6 не оптимальний, оскільки D1 = –2М – 3 < 0, D2 = –6М – 1 < 0. Вводимо в базис х 2, оскільки D2 найменше від’ємне. Виводимо з базису х 7, оскільки q4 = 1 найменше додатнє. 5. Перехід до наступної ітерації Заповнюємо наступну симплекс-таблицю, перераховуючи її елементи за правилами Жорданових виключень з головним елементом аrk (ark = а42 = 6).
Зауваження. Після виведення з базису штучної змінної х 7 можна стовбчик при змінній х 7 не обчислювати.
План х 3 = 2, х 4 = 5, х 5 = 2, х 2 = 1 не оптимальний, оскільки D1 = –16/6 < 0, D6 = –1/6 < 0. Вводимо в базис х 1, оскільки D1 найменше від’ємне. Виводимо з базису х 3, оскільки q1 = 12/8 найменше додатнє. Заповнюємо наступну симплекс-таблицю, перераховуючи її елементи за правилами Жорданових виключень з головним елементом аrk (ark = а 11= 8/6).
План х 1 =12/8, х 2 = 4/8, х 4 = 36/8, х 5 = 36/8 не оптимальний, оскільки D6 = –4/8 < 0. Вводимо в базис х 6, оскільки D6 від’ємне. Виводимо з базису х 4, оскільки Заповнюємо наступну симплекс-таблицю, перераховуючи її елементи за правилами Жорданових виключень з головним елементом аrk (ark = а 26= 3/8).
План х 1 = 3, х 2 = 2, х 3 = 0, х 4 = 0, х 5 = 3, х 6 = 12 оптимальний, оскільки D j ³ 0, j =
ЛАБОРАТОРНА РОБОТА № 7
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 .
.
 – коефіціенти при j -й змінній в функції мети, а сi – коефіцієнти функції мети при базисних змінних.
– коефіціенти при j -й змінній в функції мети, а сi – коефіцієнти функції мети при базисних змінних.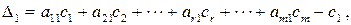
 .
.
 .
. є оптимальний розв'язок, а значення
є оптимальний розв'язок, а значення 
 (
( ) необхідно перейти до наступного допустимого базисного розв'язку або встановити, що задача не має оптимального розв’язку.
) необхідно перейти до наступного допустимого базисного розв'язку або встановити, що задача не має оптимального розв’язку. .
. – в базис вводимо xk.
– в базис вводимо xk. .
.
 – мінімальне. Це значить, що з базису виводимо змінну xr.
– мінімальне. Це значить, що з базису виводимо змінну xr. і в стовбчику xk всі елементи aik
і в стовбчику xk всі елементи aik  0, то функція мети не обмежена зверху на ОДР (області допустимих розв’язків).
0, то функція мети не обмежена зверху на ОДР (області допустимих розв’язків). .
. 2.
2. 


 4.
4. 


 6.
6. 


 8.
8. 

 10.
10. 


 12.
12. 




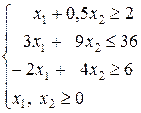 16.
16. 
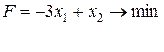

 18.
18. 

 20.
20. 

 22.
22. 

 24.
24. 


 26.
26. 

 28.
28. 


 30.
30. 

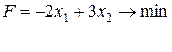
 32.
32. 
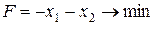

 34.
34. 
 36.
36. 


 38.
38. 
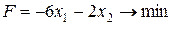
 40.
40. 
 42.
42. 
 44.
44. 


 46.
46. 

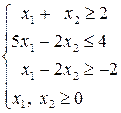 48.
48. 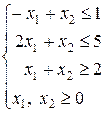


 50.
50. 

 ,
,  ,
,  відповідно, а від лівої частини четвертої нерівності віднімемо
відповідно, а від лівої частини четвертої нерівності віднімемо  , які ввійдуть у функцію мети з коефіцієнтом 0;
, які ввійдуть у функцію мети з коефіцієнтом 0;


 найменьше додатнє.
найменьше додатнє. . Z max = 11.
. Z max = 11.


