
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы n линейных уравнений с n неизвестными.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Методы их решения Рассмотрим систему n линейных уравнений с n неизвестными.
а21х1 + а22х2 + … + а2nxn = b2 (1) ………………………………. аn1х1 + аn2х2 + … + аnnxn = bn
Определение: Решением системы (1) называется совокупность чисел (х1, х2, …, хn), которая обращает каждое уравнение системы в верное равенство. Матрица А, составленная из коэффициентов при неизвестных, называется основной матрицей системы (1). A = Матрица В, состоящая из элементов матрицы А и столбца свободных членов системы (1), называется расширенной матрицей. В =
Матричный метод Рассмотрим матрицы Х = С = Тогда по правилу умножения матриц систему (1) можно представить в виде матричного уравнения А × Х = С (2) Решение уравнения (2) изложено выше, то есть Х = А-1 × С, где А-1 – обратная матрица для основной матрицы системы (1). Решить системы уравнений матричным методом: 59. 61. 63. Метод Крамера
Система n линейных уравнений с n неизвестными, главный определитель которой отличен от нуля, всегда имеет решение и притом единственное, которое находится по формулам:
где D = det А – определитель основной матрицы А системы (1), который называется главным, Dхi получаются из определителя D заменой i-ого столбца столбцом из свободных членов, т. е. D = Dх1 = Dх2 = Dхn = Пример. Решить систему уравнений методом Крамера:
х1 + х2 + 5х3 = 16 3х1 - 2х2 + х3 = 1 Решение. Вычислим определитель основной матрицы системы D = det A = Вычислим вспомогательные определители Dх1 = Dх2 = Dх3 = По формулам Крамера найдем неизвестные
Таким образом, х1 = 0; х2 = 1; х3 = 3.
Решить системы уравнений методом Крамера: 65. 67. 69. 71. 73. Метод Гаусса Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы, т.е. приведении основной матрицы системы к треугольному виду, когда под ее главной диагональю стоят нули. Это достигается с помощью элементарных преобразований матрицы над строчками. В результате таких преобразований не нарушается равносильность системы, и она приобретает также треугольный вид, т. е. последнее уравнение содержит одну неизвестную, предпоследнее – две и т. д. Выражают из последнего уравнения n-ую неизвестную и с помощью обратного хода, используя ряд последовательных подстановок, получают значения всех неизвестных.
Пример. Решить систему уравнений методом Гаусса
2х1 - х2 + 2х3 = 8. х1 + 4х2 - 3х3 = 9 Решение. Выпишем расширенную матрицу системы и приведем содержащуюся в ней матрицу А к треугольному виду. В = Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных выражений при последующих вычислениях В ~ Первую строку полученной матрицы умножим последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом В будет иметь вид: В ~. После умножения второй строки на В ~ Далее, умножая вторую строку матрицы на 10 и складывая с третьей, окончательно получим: В ~ Восстановим из полученной матрицы В систему уравнений, равносильную данной
х2 - 2х3 = 0 - 10х3 = -10 Из последнего уравнения находим После подстановки х3 = 1 и х2 = 2 в первое уравнение для х1 получим х1 = 9 - 4х2 + 3х3 = 9 - 4 × 2 + 3 × 1 = 4. Итак, х1 = 4, х2 = 2, х3 = 1. Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно. Проверка:
2 × 4 - 2 + 2 × 1 = 8 верно 4 + 4 × 2 - 3 × 1 = 9 верно Итак, система решена верно. Решить системы уравнений методом Гаусса: 75. 77. 79. 81. 83.
Метод Жордана-Гаусса Суть метода Жордана-Гаусса состоит в полном исключении переменных из каждого уравнения системы, кроме единственной, т. е. основная матрица системы приводится с помощью элементарных преобразований над строчками к единичной матрице и система (1) приобретает следующий вид:
откуда видно, что неизвестные х1; х2;…; хn равны соответствующим свободным членам в1'; в2';…; вn', т.е. решением системы уравнений (1) является набор чисел (в1'; в2';…; вn').
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 3938; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.110.198 (0.01 с.) |

 а11х1 + а12х2 + … + а1nxn = b1
а11х1 + а12х2 + … + а1nxn = b1 .
.
 – матрица неизвестных;
– матрица неизвестных; – матрица свободных членов системы (1).
– матрица свободных членов системы (1). 60.
60. 
 62.
62. 
 . 64.
. 64.  .
. ,
, ;
; ;
; ;
;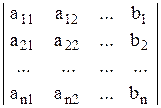 ;
; 2х1 + 3х2 + 4х3 = 15
2х1 + 3х2 + 4х3 = 15 = 44 ¹ 0
= 44 ¹ 0 = 0;
= 0; = 44;
= 44; = 132.
= 132. ;
;  ;
;  .
. . 66.
. 66.  .
. . 68.
. 68.  .
. . 70.
. 70. 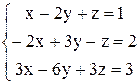 .
. . 72.
. 72. 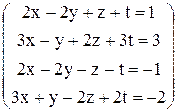 .
. . 74.
. 74.  .
. 3х1 + 2х2 + х3 = 17
3х1 + 2х2 + х3 = 17 .
. .
.
 и сложения ее с третьей строкой матрица А примет треугольный вид. Однако, чтобы упростить вычисления, можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим:
и сложения ее с третьей строкой матрица А примет треугольный вид. Однако, чтобы упростить вычисления, можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим: .
. .
. х1 + 4х2 - 3х3 = 9
х1 + 4х2 - 3х3 = 9 Найденное значение х3 = 1 подставим во второе уравнение системы, из которого х2 = 2х3 = 2 × 1 = 2.
Найденное значение х3 = 1 подставим во второе уравнение системы, из которого х2 = 2х3 = 2 × 1 = 2. 3 × 4 + 2 × 2 + 1 = 17 верно
3 × 4 + 2 × 2 + 1 = 17 верно . 76.
. 76.  .
.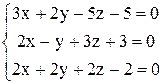 . 78.
. 78. 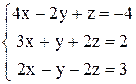 .
. . 80.
. 80.  .
. . 82.
. 82.  .
. . 84.
. 84.  .
.



