
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм построения обратной матрицыСодержание книги Поиск на нашем сайте
Для построения матрицы А-1, обратной матрице А, нужно: 1. Вычислить определитель матрицы А, причем det А ¹ 0 2. Найти алгебраические дополнения элементов аij матрицы А и составить матрицу дополнений Ад. 3. Составить союзную матрицу А*, транспонируя матрицу Ад. 4. Составить обратную матрицу
Пример. Найти обратную матрицу А-1, если А= Решение. Вычислим определитель матрицы А: det A= Найдем алгебраические дополнения элементов матрицы А. а11 = 2, М11 = а12 = 1, М12 = а13 = 3, М13 = а21 = –1, М21 = а22 = 0, М22 = а23 = 4, М23 = а31 = 5, М31 = а32 = 1, М32 = а33 = 1, М33 = Составим матрицу дополнений Ад = Найдем союзную матрицу А* = (Ад)т = Построим обратную матрицу
Найти обратную матрицу для следующих матриц: 32. 35. 38. 41.
Простейшие матричные уравнения
Рассмотрим матрицы
причем элементы матриц А и В заданы, а Х1, Х2, Х3 – неизвестные. Тогда уравнение А × Х = В называется простейшим матричным уравнением. Чтобы его решить, т. е. найти элементы матрицы неизвестных Х, поступим следующим образом: 1. Умножим обе части уравнения на матрицу А-1, обратную для матрицы А, слева: А-1 (А × Х) = А-1 × В. 2. Используя свойство умножения матриц, запишем (А-1 × А) Х = А-1 × В. 3. Из определения обратной матрицы (А-1 × А = Е) имеем Е × Х = А-1 × В. 4. Используя свойство единичной матрицы (Е × Х = Х), окончательно получим Х = А-1 × В. Замечание. Если матричное уравнение имеет вид Х × С = Д, то для нахождения неизвестной матрицы Х уравнение необходимо умножать на С-1 справа. Пример. Решить матричное уравнение
Решение. Введем обозначения А = Из определения умножения матриц с учетом размерностей А и В матрица неизвестных Х будет иметь вид Х = С учетом введенных обозначений имеем А × Х = В, откуда Х = А-1 × В. Найдем А-1 по алгоритму (см.)
Вычислим произведение
Тогда для Х получим Х = Решить матричные уравнения: 44. 46. 48. 50. 51. 52.
Ранг матрицы
Рассмотрим матрицу А размера (m x n)
Минором k-ого порядка матрицы А будем называть определитель порядка к, элементами которого являются элементы матрицы А, стоящие на пересечении любых k строк и любых k столбцов. Очевидно k £ min (m, n). Определение. Рангом r(A) матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля. Определение. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется базисным минором. Определени е. Матрицы, имеющие одинаковые ранги, называются эквивалентными. Вычисление ранга матрицы Определение. Матрица называется ступенчатой, если под первым ненулевым элементом каждой ее строки стоят нули в нижележащих строках. Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк. Таким образом, преобразуя матрицу к ступенчатому виду, несложно определить ее ранг. Эта операция осуществляется с помощью элементарных преобразований матрицы, которые не изменяют ее ранга. Умножение всех элементов ряда матрицы на число l ¹ 0; – замена строк столбцами и наоборот; – перестановка местами параллельных рядов; – вычеркивание нулевого ряда; – прибавление к элементам некоторого ряда соответствующих элементов параллельного ряда, умноженных на любое действительное число. Пример. Вычислить ранг матрицы А = Решение. Преобразуем матрицу к ступенчатому виду. Для этого к третьей строке прибавим вторую, умноженную на (–3). А ~
К четвертой строке прибавим третью.
Число ненулевых строк в полученной эквивалентной матрице равно трем, следовательно, r(А) = 3. Определить ранг матрицы: 53. 55. 57.
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.119.222 (0.01 с.) |


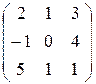
 = 10 ¹ 0
= 10 ¹ 0 = –4, А11 = (–1)1+1 (–4) = –4
= –4, А11 = (–1)1+1 (–4) = –4 = –21, А12 = (–1)1+2 ×(–1) = 21
= –21, А12 = (–1)1+2 ×(–1) = 21 = -1, А13 = (–1)1+3 ×1 = –1
= -1, А13 = (–1)1+3 ×1 = –1 = –2, А21 = (–1)2+1× (–2) = 2
= –2, А21 = (–1)2+1× (–2) = 2 =–13, А22 = (–1)2+2 × (–13) = –13
=–13, А22 = (–1)2+2 × (–13) = –13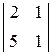 = –3, А23 = (–1)2+3 × (–3) = 3
= –3, А23 = (–1)2+3 × (–3) = 3 = 4, А31 = (–1)3+1× 4 = 4
= 4, А31 = (–1)3+1× 4 = 4 = 11, А32 = (–1)3+2 × 11 = –11
= 11, А32 = (–1)3+2 × 11 = –11 = 1, А33 = (–1)3+3 × 1 = 1
= 1, А33 = (–1)3+3 × 1 = 1 .
.
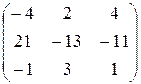 .
.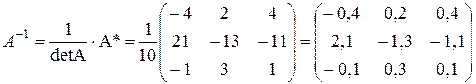 .
.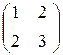 . 33.
. 33.  . 34.
. 34.  .
. . 36.
. 36.  . 37.
. 37.  .
.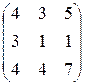 . 39.
. 39.  . 40.
. 40.  .
. . 42.
. 42. 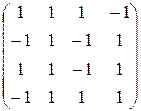 . 43.
. 43.  .
.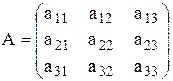 ;
; 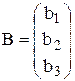 ;
; 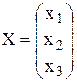 ,
, .
.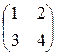 ; В =
; В = 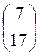 .
.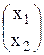 .
.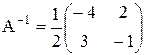
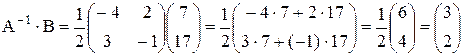
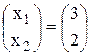 откуда х1 = 3, х2 = 2
откуда х1 = 3, х2 = 2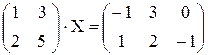 . 45.
. 45. 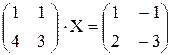 .
.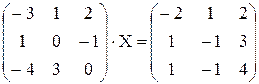 . 47.
. 47. 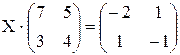 .
.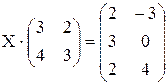 . 49. X
. 49. X 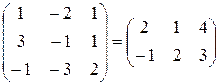 .
.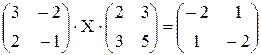 .
.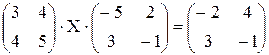 .
.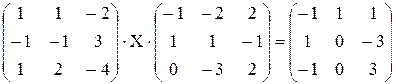 .
. .
.
 .
. А ~
А ~ 
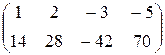 . 54.
. 54.  .
.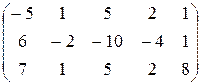 . 56.
. 56.  .
.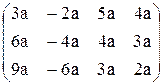 . 58.
. 58.  .
.


