
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие общего решения системы уравнений ⇐ ПредыдущаяСтр 6 из 6
Рассмотрим систему уравнений (2) и будем считать, что она совместна, т.е. r(А) = r(В) = r и пусть r< n. Рассмотрим какой-нибудь базисный минор основной матрицы А, выделим в нем произвольную строку, элементы которой есть коэффициент при r неизвестных в одном из уравнений системы. Эти неизвестные, например, х1, х2, …, хr, назовем базисными, тогда остальные (n-r) неизвестных, т.е. хr+1, хr+2, …, хn назовем свободными переменными. Выразим все базисные неизвестные через свободные в выбранной системе r уравнений, получим:
Присвоим свободным переменным произвольные действительные значения сi, где Количество наборов r базисных неизвестных из n переменных определяется числом базисных миноров. Пример. Исследовать систему уравнений на совместность и найти ее общее решение.
2х1 - х2 + 2х3 - х4 = 0 5х1 + 3х2 + 8х3 + х4 = 1 Решение. Определим ранги матриц А и В, для чего выпишем расширенную матрицу В и приведем ее к ступенчатому виду В = Умножим последовательно первую строку на (-2) и (-5) и сложим соответственно со второй и третьей строками. Получим эквивалентную матрицу В ~ К третьей строке прибавим вторую, умноженную на (-2), тогда
Число ненулевых строк матриц А и В равно двум, r(А) = r(В) = r = 2, следовательно по теореме Кронекера-Капелли система совместна, но т. к. r = 2 < n = 4, она имеет бесконечное множество решений. Ранг системы r = 2, а это значит, что базисные миноры матрицы А имеют порядок, равный двум, каждый из которых определяет набор базисных неизвестных. Выпишем базисные миноры матрицы А М1 = М2 = М3 = М4 = М5 = М6 = Таким образом, существует шесть вариантов общего решения системы уравнений. Для примера рассмотрим первый вариант, соответствующий базисному минору М1. а) х1 и х2 – базисные неизвестные; х3 и х4 – свободные переменные. Пусть х3 = с1, х4 = с2, с1, с2 Î R. Из ступенчатой матрицы В восстановим систему уравнений, равносильную исходной
-11х2 - 6х3 - 7х4 = -2 Умножим второе уравнение на (–1) и с учетом введенных обозначений перепишем систему в виде
11х2 = 2 - 6с1 - 7с2 Выразим базисные неизвестные х1 и х2 через свободные переменные. Так как система уравнений имеет треугольный вид, ее удобно решать методом Гаусса. Из последнего уравнения находим
Подставляя это значение х2 в первое уравнение для х1, получим
Таким образом, первый вариант общего решения будет иметь вид
Исследовать совместность системы уравнений и найти ее общее решение:
91. 93. 95. 97. 99. 100.
Ответы 1. 4. АВ = 8. 11. 13. А·В·С = 33. 37. 40. 42. 44. 47. 51. 58. r = 1, если а = 1; r = 2, если а = –2; r = 3, если а ¹ 1 и а ¹ –2; 59. (3; 1; 1); 60. (1; 4; –2); 61. (–1; 0; 1); 62. (1; –1; 2); 63. (1; 3; 4); 64. (0; 1; 2); 65. (1; 1; 2); 66. (1; 1; 1); 67. (1; 2; 3); 68. (2; 0; 1); 69. 70. Бесконечное множество решений; 71. (2; 1; –1; 3); 72. (1; 1; 2; –1); 73. (1; 2; 3; 4); 74. (–2; 0; 2; 1); 75. (3; 2; 1); 76. (2; 1; 2); 77. (–2; 2; 1); 78. (1; 3; –2); 79. (1; 0; 3); 80. (2; 4; 3); 81. (2; –1; 2; 1); 82. (1; –4; 2; –3); 83. (1; 1; –1; –1); 84. (2; 1; 1; 1); 85. (–1; –3; 4); 86. (–1; 3; 1); 87. (–9; –10; 13); 88. (3; 1; 2); 89. (1; 1; –1; –1); 90. (3; 2; 0; 1); 91. r = 2,(2 + с1 – 2с2; 1 – 2с1 – с2; с1; с2); 92. r = 2, (8 – 9с1 – 4с2; с1; с2; –10 + 11с1 + 5с2); 93. r = 2, ( с1;с2; 11с1 – 11с2 – 11;–8с1 + 8с2 + 8); 94. r = 3, (2 + с1 – 1 – 2с; 2с; с); 95. Несовместна; 96. r = 3, (5 – 2с; 98. Несовместна; 99. r = 2, (с1; с2; – 6 + 5с1 + с2 – с3; с3; –1 + с1); 100. r = 3, (–9 – с1 – с2; с1; с2; –7 + 2с2; 3 + 2с2).
Список рекомендуемой литературы 1. Высшая математика для экономистов / Под ред. проф. Н.Ш. Крамера. – М., 1997. 2. Общий курс высшей математики для экономистов /Под ред. проф. В.И. Ермакова. – М., 2001. 3. Щипачев В.С. Высшая математика / В.С. Щипачев. – М., 2001. 6. Сборник задач по высшей математике для экономистов / Под ред. проф. В.И. Ермакова. – М., 2002.
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ ПО ЛИНЕЙНОЙ АЛГЕБРЕ
Составители: Коровин Анатолий Геннадьевич Кокорина Елена Васильевна
Редактор Н.С. Шубина Компьютерный набор Н.М. Болотова
Сдано в набор 21.04.2005. Подписано к печати 28.06.2005. Формат 60х84 1/16. Бумага Data Copy. Гарнитура Таймс. Усл.-печ.л. 2,5. Тираж экз. Заказ №.
Нижегородский коммерческий институт 603140, г. Н. Новгород, пр. Ленина, 27.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.228 (0.019 с.) |

 , тогда получим общее решение системы уравнений (х1, х2, …, хr, с1, с2, …, сn-r)
, тогда получим общее решение системы уравнений (х1, х2, …, хr, с1, с2, …, сn-r)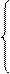 х1 + 5х2 + 4х3 + 3 х4 = 1
х1 + 5х2 + 4х3 + 3 х4 = 1




 В ~
В ~ 
 = –1 ¹ 0, х1, х2 – первый набор базисных неизвестных;
= –1 ¹ 0, х1, х2 – первый набор базисных неизвестных; = –6 ¹ 0, х1, х3 – второй набор базисных неизвестных;
= –6 ¹ 0, х1, х3 – второй набор базисных неизвестных; = –7 ¹ 0, х1, х4 – третий набор базисных неизвестных;
= –7 ¹ 0, х1, х4 – третий набор базисных неизвестных; = 14 ¹ 0, х2, х3 – четвертый набор базисных неизвестных;
= 14 ¹ 0, х2, х3 – четвертый набор базисных неизвестных; = –2 ¹ 0, х2, х4 – пятый набор базисных неизвестных;
= –2 ¹ 0, х2, х4 – пятый набор базисных неизвестных; = –10 ¹ 0, х3, х4 – шестой набор базисных неизвестных.
= –10 ¹ 0, х3, х4 – шестой набор базисных неизвестных. х1 + 5х2 + 4х3 + 3х4 = 1
х1 + 5х2 + 4х3 + 3х4 = 1 .
. .
. .
. 92.
92. 
 . 94.
. 94.  .
. . 96.
. 96.  .
. . 98.
. 98.  .
. .
. .
. ; 2.
; 2.  ; 3. 49;
; 3. 49; , ВА =
, ВА =  ; 5.
; 5. 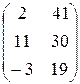 ; 6.
; 6.  ; 7. 7;
; 7. 7; ; 9.
; 9.  ; 10.
; 10.  ;
; ; 12. ( АВ)·С=А·(ВС)=
; 12. ( АВ)·С=А·(ВС)=  ;
; , А·С·В не существует, В·А·С не существует, В·С·А =
, А·С·В не существует, В·А·С не существует, В·С·А =  , С·А·В =
, С·А·В =  , С·В·А не существует; 14. –25; 15. 14; 16. –36; 17. –1; 18. –20; 19. 5; 20. –3; 21. 6; 22. 16; 23. –360; 24. 117; 25. 234; 26. 0; 27. 21; 28. –230; 29. –222; 30. –322; 31. 57; 32.
, С·В·А не существует; 14. –25; 15. 14; 16. –36; 17. –1; 18. –20; 19. 5; 20. –3; 21. 6; 22. 16; 23. –360; 24. 117; 25. 234; 26. 0; 27. 21; 28. –230; 29. –222; 30. –322; 31. 57; 32.  ;
; ; 34.
; 34.  ; 35.
; 35.  ; 36.
; 36.  ;
; ; 38.
; 38.  ; 39.
; 39.  ;
; ; 41.
; 41.  ;
; ; 43.
; 43.  ;
; ; 45.
; 45.  ; 46.
; 46.  ;
; ; 48.
; 48.  ; 49.
; 49.  ; 50.
; 50. 
 ; 52.
; 52.  ; 53. 2; 54. 2; 55. 3; 56. 4; 57. 2;
; 53. 2; 54. 2; 55. 3; 56. 4; 57. 2; ;
; (7 – 5с; с;
(7 – 5с; с; 


