
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие определителей матрицСтр 1 из 6Следующая ⇒
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ ПО ЛИНЕЙНОЙ АЛГЕБРЕ Нижний Новгород
УДК 517 ББК 22.1я73
Сборник задач и упражнений по линейной алгебре / Сост. А.Г. Коровин, Е.В. Кокорина. – Н. Новгород: НКИ, 2005. – 41 с.
Отв. редактор: зав. кафедрой высшей математики, д. техн. н., профессор Б.И. Вайсблат.
Настоящее пособие содержит методические указания и основные теоретические сведения, необходимые для решения задач по отдельным темам линейной алгебры. Его цель – закрепить теоретические знания, полученные при изучении данного раздела курса высшей математики, и дать умения и навыки решения задач по данному разделу. Пособие предназначено для студентов дневного отделения экономических и коммерческих специальностей.
ã Нижегородский коммерческий институт, 2005 ã Составление, Коровин А.Г., Кокорина Е.В., 2005
Понятие матриц Определение 1. Матрицей размера (m х n) (m и n – натуральные числа) называется совокупность чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Строки и столбцы матрицы называются рядами.
Элементы матрицы обозначают aij, где i – номер строки, j – номер столбца. Если в матрице А m = n, то она называется квадратной порядка n и записывается
Элементы а11, а22, …, аnn образуют главную диагональ матрицы Аn. Виды квадратных матриц:
Вn – треугольная матрица; Dn – диагональная матрица; En – единичная матрица; Оn – нулевая матрица. Операции над матрицами
Определение 2. Матрицы одного размера А = (аij) и В = (bij) называются равными, если равны их соответствующие элементы, т. е. аij = bij.
Сложение матриц Определение 3. Суммой (разностью) матриц А = (аij) и В = (bij) одного размера называется матрица С, элементы которой равны суммам (разностям) соответствующих элементов матриц А и В, т.е. сij = аij + bij Пример. Найти сумму матриц× А = Решение С = А + В = Операция сложения матриц обладает следующими свойствами: 1. А + В = В + А; 2. (А + В) + С = А + (В + С).
Умножение матрицы на число Определение 4. Произведением матрицы А = (аij) на вещественное число У называется матрица С = (сij) той же размерности, элементы которой равны произведению числа k на соответствующие элементы матрицы А, т. е. сij = k × аij.
Пример. Найти произведение матрицы А = Решение. С = k × А = Операция умножения матрицы на число обладает свойствами: 1. a(bА) = (ab)А; 2. a(А+В) = aА + aВ; 3. (a+b)А = aА + bА, (a и b – действительные числа). Умножение матриц Определение 5. Произведением матрицы А = (аip) размера (m x n) на матрицу В = (bpj) размера (n x p) называется матрица С = (сij) размера (m x p), элементы которой равны сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В, т. е. сij = аi1b1j + аi2b2j +… + аiрbрj (1) Причем матрицу А можно умножать на матрицу В тогда и только тогда, когда число столбцов матрицы А равно числу строк матрицы В. Пример. Найти произведение матриц А = Решение. Размер матрицы А - (2 х 3), размер матрицы В - (3 х 2). Число столбцов А равно числу строк В: умножение возможно. При этом размер матрицы С = А × В - (2 × 2). Найдем элементы сij матрицы С по формуле (1). с11 = а11b11 + а12b21 +а13b31 = 1 × 1 + 2 × 0 + 0 × 2 = 1; с12 = а11b12 + а12b22 +а13b32 = 1 × 2 + 2 × 1 + 0 × 2 = 4; с21 = а21b11 + а22b21 +а23b31 = 3 × 1 + 1 × 0 + 1 × 2 = 5; с22 = а21b12 + а22b22 +а23b32 = 3 × 2 + 1 × 1 + 1 × 2 = 9. Таким образом, С = Операция умножения матриц обладает следующими свойствами: 1. (АВ)С = А(ВС); 2. (А + В)С = АС + ВС; 3. В общем случае АВ ¹ ВА. Замечание: Свойством коммутативности обладают произведения А×Е = Е×А = А, А×О = О×А = О, где Е и О – единичная и нулевая матрицы соответственно. Транспонирование матрицы Определение 6. Если в матрице А = (аij) размера (m х n) строчки и столбцы поменять местами, то полученная при этом матрица Ат = (аji) размера (n х m) называется транспонированной. Пример. Транспонировать матрицу А = Решение. Операция транспонирования матрицы А осуществляется следующим образом: первая строка матрицы А становится первым столбцом матрицы Ат, вторая строка А – вторым столбцом Ат, т. е. Ат =
1. Выполнить следующие действия: 2·
2. Решить уравнение 5·А + 2Х – В = 0, где А =
3. Найти элемент С32 матрицы С = А·В, если А = 4. Вычислить А·В и В·А, если А = Вычислить произведение матриц: 5. 7. 9.
Вычислить: 11. 3 А·В – 2 В·А, если
А = 12. (А·В)·С и А·(В·С), если А = 13. Вычислить все возможные произведения матриц А, В и С, если А = Решение. det A = Определитель матрицы А = (аij) третьего порядка вычисляется по правилу треугольников (Сарруса)
Пример. Вычислить определитель матрицы А = Решение. Для вычисления определителя воспользуемся правилом треугольников. det A = Свойства определителей 1. Определитель произведения матриц равен произведению определителей перемножаемых матриц, т. е. det (A × B) = det A × det B. 2. Определитель транспонированной матрицы равен определителю исходной матрицы, т. е. det A = det Aт 3. При перестановке двух параллельных рядов местами определитель изменяет свой знак на противоположный. 4. Общий множитель элементов одного ряда можно вынести за знак определителя. 5. Определитель, имеющий два одинаковых параллельных ряда, равен нулю. 6. Если элементы двух параллельных рядов определителя пропорциональны, то он равен нулю. 7. Если определитель имеет ряд из одних нулей, то он равен нулю. 8. Если к элементам какого-либо ряда определителя прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число, то определитель не изменит своей величины. 9. Треугольный определитель, у которого все элементы, лежащие ниже (выше) главной диагонали, – нули, равен произведению элементов главной диагонали.
Решение. Обратим все элементы первого столбца определителя в нуль, кроме первого (а11 = 1). Для чего элементы первой строки умножим последовательно на (–3), (–1) и 2 и сложим соответственно с элементами второй, третьей и четвертой строк.
Вынесем за знак определителя 2 – общий множитель элементов четвертой строки и разложим определитель по элементам первого столбца.
Отличным от нуля является лишь первое слагаемое, поэтому D = 2 × а11А11 = 2 × 1 × (–1)1+1 × М11 = 2 Вычисляя определитель третьего порядка по правилу треугольников, окончательно получим: D = 2 × (–24) = –48.
2. Преобразование определителя к треугольному виду Данный метод основан на использовании свойства 9 определителей. Пример. Вычислить определитель
Решение. Используя свойство 8, преобразуем определитель к треугольному виду, т. е. так, чтобы под его главной диагональю стояли нули. Элементы первой строки умножим последовательно на (–3), (–1) и 2 и сложим соответственно с элементами второй, третьей и четвертой строк.
Вынесем за знак определителя 2 – общий множитель элементов четвертой строки – и поменяем местами вторую и третью строки.
Вторую строку умножим последовательно на (–7) и 3 и сложим соответственно с третьей и четвертой строками.
Вынесем за знак определителя 3 и 2 – общие множители элементов третьей и четвертой строк соответственно.
К элементам четвертой строки прибавим соответствующие элементы третьей.
Перемножая элементы главной диагонали полученного треугольного определителя, окончательно получим: D = –12 × 4 = – 48 Вычислить определители: 14. 17. 20. 23. 26. 29.
31. Обратная матрица
Определение. Квадратная матрица А называется вырожденной, если ее определитель равен нулю, и невырожденной, если ее определитель отличен от нуля. Определение. Матрица А-1 называется обратной для матрицы А, если выполняется условие А-1 × А = А × А-1 = Е. Для составления обратной матрицы введем следующие понятия: 1. Ад – матрица дополнений, которая состоит из алгебраических дополнений каждого элемента матрицы А. 2. А* – союзная или присоединенная матрица, которая является транспонированной для матрицы дополнений, т. е. А* = (Ад)т. Теорема. Если матрица невырожденная, то обратная для нее матрица А-1 вычисляется по формуле
Решение. Вычислим определитель матрицы А: det A= Найдем алгебраические дополнения элементов матрицы А. а11 = 2, М11 = а12 = 1, М12 = а13 = 3, М13 = а21 = –1, М21 = а22 = 0, М22 = а23 = 4, М23 = а31 = 5, М31 = а32 = 1, М32 = а33 = 1, М33 = Составим матрицу дополнений Ад = Найдем союзную матрицу А* = (Ад)т = Построим обратную матрицу
Найти обратную матрицу для следующих матриц: 32. 35. 38. 41.
Ранг матрицы
Рассмотрим матрицу А размера (m x n)
Минором k-ого порядка матрицы А будем называть определитель порядка к, элементами которого являются элементы матрицы А, стоящие на пересечении любых k строк и любых k столбцов. Очевидно k £ min (m, n). Определение. Рангом r(A) матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля. Определение. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется базисным минором. Определени е. Матрицы, имеющие одинаковые ранги, называются эквивалентными. Вычисление ранга матрицы Определение. Матрица называется ступенчатой, если под первым ненулевым элементом каждой ее строки стоят нули в нижележащих строках. Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк. Таким образом, преобразуя матрицу к ступенчатому виду, несложно определить ее ранг. Эта операция осуществляется с помощью элементарных преобразований матрицы, которые не изменяют ее ранга. Умножение всех элементов ряда матрицы на число l ¹ 0; – замена строк столбцами и наоборот;
– перестановка местами параллельных рядов; – вычеркивание нулевого ряда; – прибавление к элементам некоторого ряда соответствующих элементов параллельного ряда, умноженных на любое действительное число. Пример. Вычислить ранг матрицы А = Решение. Преобразуем матрицу к ступенчатому виду. Для этого к третьей строке прибавим вторую, умноженную на (–3). А ~
К четвертой строке прибавим третью.
Число ненулевых строк в полученной эквивалентной матрице равно трем, следовательно, r(А) = 3. Определить ранг матрицы: 53. 55. 57.
Методы их решения Рассмотрим систему n линейных уравнений с n неизвестными.
а21х1 + а22х2 + … + а2nxn = b2 (1) ………………………………. аn1х1 + аn2х2 + … + аnnxn = bn
Определение: Решением системы (1) называется совокупность чисел (х1, х2, …, хn), которая обращает каждое уравнение системы в верное равенство. Матрица А, составленная из коэффициентов при неизвестных, называется основной матрицей системы (1). A = Матрица В, состоящая из элементов матрицы А и столбца свободных членов системы (1), называется расширенной матрицей. В =
Матричный метод Рассмотрим матрицы Х = С = Тогда по правилу умножения матриц систему (1) можно представить в виде матричного уравнения А × Х = С (2) Решение уравнения (2) изложено выше, то есть Х = А-1 × С, где А-1 – обратная матрица для основной матрицы системы (1). Решить системы уравнений матричным методом: 59. 61. 63. Метод Крамера
Система n линейных уравнений с n неизвестными, главный определитель которой отличен от нуля, всегда имеет решение и притом единственное, которое находится по формулам:
где D = det А – определитель основной матрицы А системы (1), который называется главным, Dхi получаются из определителя D заменой i-ого столбца столбцом из свободных членов, т. е. D = Dх1 = Dх2 = Dхn = Пример. Решить систему уравнений методом Крамера:
х1 + х2 + 5х3 = 16 3х1 - 2х2 + х3 = 1 Решение. Вычислим определитель основной матрицы системы D = det A = Вычислим вспомогательные определители Dх1 = Dх2 = Dх3 = По формулам Крамера найдем неизвестные
Таким образом, х1 = 0; х2 = 1; х3 = 3.
Решить системы уравнений методом Крамера: 65. 67. 69. 71. 73. Метод Гаусса Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы, т.е. приведении основной матрицы системы к треугольному виду, когда под ее главной диагональю стоят нули. Это достигается с помощью элементарных преобразований матрицы над строчками. В результате таких преобразований не нарушается равносильность системы, и она приобретает также треугольный вид, т. е. последнее уравнение содержит одну неизвестную, предпоследнее – две и т. д. Выражают из последнего уравнения n-ую неизвестную и с помощью обратного хода, используя ряд последовательных подстановок, получают значения всех неизвестных.
Пример. Решить систему уравнений методом Гаусса
2х1 - х2 + 2х3 = 8. х1 + 4х2 - 3х3 = 9 Решение. Выпишем расширенную матрицу системы и приведем содержащуюся в ней матрицу А к треугольному виду. В = Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных выражений при последующих вычислениях В ~ Первую строку полученной матрицы умножим последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом В будет иметь вид: В ~. После умножения второй строки на В ~ Далее, умножая вторую строку матрицы на 10 и складывая с третьей, окончательно получим: В ~ Восстановим из полученной матрицы В систему уравнений, равносильную данной
х2 - 2х3 = 0 - 10х3 = -10 Из последнего уравнения находим После подстановки х3 = 1 и х2 = 2 в первое уравнение для х1 получим х1 = 9 - 4х2 + 3х3 = 9 - 4 × 2 + 3 × 1 = 4. Итак, х1 = 4, х2 = 2, х3 = 1. Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно. Проверка:
2 × 4 - 2 + 2 × 1 = 8 верно 4 + 4 × 2 - 3 × 1 = 9 верно Итак, система решена верно. Решить системы уравнений методом Гаусса: 75. 77. 79. 81. 83.
Метод Жордана-Гаусса Суть метода Жордана-Гаусса состоит в полном исключении переменных из каждого уравнения системы, кроме единственной, т. е. основная матрица системы приводится с помощью элементарных преобразований над строчками к единичной матрице и система (1) приобретает следующий вид:
откуда видно, что неизвестные х1; х2;…; хn равны соответствующим свободным членам в1'; в2';…; вn', т.е. решением системы уравнений (1) является набор чисел (в1'; в2';…; вn').
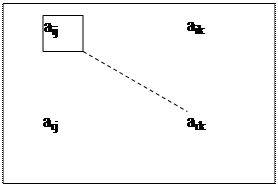
Правило прямоугольника Пусть в матрице А системы аij – разрешающий элемент, а пересчитываемый элемент аrk, тогда можно рассмотреть прямоугольник,
где разрешающий и искомый элементы лежат на одной его диагонали, называемой главной. Новое значение а'rk пересчитываемого элемента аrk вычисляется по формуле а'rk = т. е. умножаем элементы главной диагонали прямоугольника, вычитаем произведение элементов другой его диагонали и результат делим на разрешающий элемент. Аналогично пересчитывается столбец свободных членов в'r Пример. Решить систему уравнений, используя алгоритм Жордана- Гаусса.
Решение. Запишем расширенную матрицу системы в виде таблицы и воспользуемся алгоритмом Жордана-Гаусса.
Таблица № 4 задает систему уравнений, равносильную данной
откуда x1 = 1; x2 = –3; x3 = 2. Решить системы уравнений методом Жордана-Гаусса. 85. 87. 89.
Ответы 1. 4. АВ = 8. 11. 13. А·В·С = 33. 37. 40. 42. 44. 47. 51. 58. r = 1, если а = 1; r = 2, если а = –2; r = 3, если а ¹ 1 и а ¹ –2; 59. (3; 1; 1); 60. (1; 4; –2); 61. (–1; 0; 1); 62. (1; –1; 2); 63. (1; 3; 4); 64. (0; 1; 2); 65. (1; 1; 2); 66. (1; 1; 1); 67. (1; 2; 3); 68. (2; 0; 1); 69. 70. Бесконечное множество решений; 71. (2; 1; –1; 3); 72. (1; 1; 2; –1); 73. (1; 2; 3; 4); 74. (–2; 0; 2; 1); 75. (3; 2; 1); 76. (2; 1; 2); 77. (–2; 2; 1); 78. (1; 3; –2); 79. (1; 0; 3); 80. (2; 4; 3); 81. (2; –1; 2; 1); 82. (1; –4; 2; –3); 83. (1; 1; –1; –1); 84. (2; 1; 1; 1); 85. (–1; –3; 4); 86. (–1; 3; 1); 87. (–9; –10; 13); 88. (3; 1; 2); 89. (1; 1; –1; –1); 90. (3; 2; 0; 1); 91. r = 2,(2 + с1 – 2с2; 1 – 2с1 – с2; с1; с2); 92. r = 2, (8 – 9с1 – 4с2; с1; с2; –10 + 11с1 + 5с2); 93. r = 2, ( с1;с2; 11с1 – 11с2 – 11;–8с1 + 8с2 + 8); 94. r = 3, (2 + с1 – 1 – 2с; 2с; с); 95. Несовместна; 96. r = 3, (5 – 2с; 98. Несовместна; 99. r = 2, (с1; с2; – 6 + 5с1 + с2 – с3; с3; –1 + с1); 100. r = 3, (–9 – с1 – с2; с1; с2; –7 + 2с2; 3 + 2с2).
Список рекомендуемой литературы 1. Высшая математика для экономистов / Под ред. проф. Н.Ш. Крамера. – М., 1997. 2. Общий курс высшей математики для экономистов /Под ред. проф. В.И. Ермакова. – М., 2001. 3. Щипачев В.С. Высшая математика / В.С. Щипачев. – М., 2001. 6. Сборник задач по высшей математике для экономистов / Под ред. проф. В.И. Ермакова. – М., 2002.
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ ПО ЛИНЕЙНОЙ АЛГЕБРЕ
Составители: Коровин Анатолий Геннадьевич Кокорина Елена Васильевна
Редактор Н.С. Шубина Компьютерный набор Н.М. Болотова
Сдано в набор 21.04.2005. Подписано к печати 28.06.2005. Формат 60х84 1/16. Бумага Data Copy. Гарнитура Таймс. Усл.-печ.л. 2,5. Тираж экз. Заказ №.
Нижегородский коммерческий институт 603140, г. Н. Новгород, пр. Ленина, 27.
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ ПО ЛИНЕЙНОЙ АЛГЕБРЕ Нижний Новгород
УДК 517 ББК 22.1я73
Сборник задач и упражнений по линейной алгебре / Сост. А.Г. Коровин, Е.В. Кокорина. – Н. Новгород: НКИ, 2005. – 41 с.
Отв. редактор: зав. кафедрой высшей математики, д. техн. н., профессор Б.И. Вайсблат.
Настоящее пособие содержит методические указания и основные теоретические сведения, необходимые для решения задач по отдельным темам линейной алгебры. Его цель – закрепить теоретические знания, полученные при изучении данного раздела курса высшей математики, и дать умения и навыки решения задач по данному разделу. Пособие предназначено для студентов дневного отделения экономических и коммерческих специальностей.
ã Нижегородский коммерческий институт, 2005 ã Составление, Коровин А.Г., Кокорина Е.В., 2005
Понятие матриц Определение 1. Матрицей размера (m х n) (m и n – натуральные числа) называется совокупность чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Строки и столбцы матрицы называются рядами.
Элементы матрицы обозначают aij, где i – номер строки, j – номер столбца. Если в матрице А m = n, то она называется квадратной порядка n и записывается
Элементы а11, а22, …, аnn образуют главную диагональ матрицы Аn. Виды квадратных матриц:
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.236.174 (0.334 с.) |
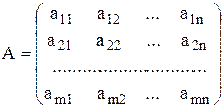
 .
. ;
;  ;
; ;
;  .
. и В =
и В = 

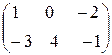 на число k = 3.
на число k = 3. .
. и В =
и В = 
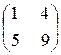 .
. .
. .
. – 3·
– 3· 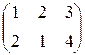 .
. ; В =
; В =  .
. ; В =
; В =  .
. ; В =
; В = 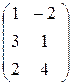 .
.
 . 6.
. 6. 
 .
.
 . 8.
. 8. 
 .
.
 . 10.
. 10. 
 .
. ; В =
; В = 
 ; В =
; В =  ; С =
; С = 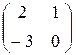 .
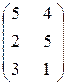
. ; В =
; В =  ; С =
; С =  /
/ = 1 × 4 - 2 × 3 = -2
= 1 × 4 - 2 × 3 = -2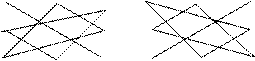 det A =
det A =  = (а11а22а33 + а12а23а31 + а21а13а32) - (а13а22а31 + а12а33а21 + а11а23а32)
= (а11а22а33 + а12а23а31 + а21а13а32) - (а13а22а31 + а12а33а21 + а11а23а32)
 = (1 × 5 × 9 + 2 × 6 × 7 + 4 × 3 × 9) - (3 × 5 × 7 + 4 × 2 × 6 + 1 × 6 × 8) = 0
= (1 × 5 × 9 + 2 × 6 × 7 + 4 × 3 × 9) - (3 × 5 × 7 + 4 × 2 × 6 + 1 × 6 × 8) = 0
 = 2 (а11А11 + а21А21 + а31А31 + а41А41).
= 2 (а11А11 + а21А21 + а31А31 + а41А41).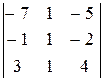 .
.

 .
. .
. .
.
 15.
15.  16.
16. 
 18.
18.  19.
19. 
 . 21.
. 21.  . 22.
. 22. 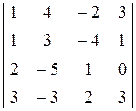 .
. . 24.
. 24. 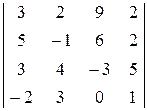 . 25.
. 25.  .
. . 27.
. 27.  . 28.
. 28.  .
. . 30.
. 30.  .
. .
. .
. = 10 ¹ 0
= 10 ¹ 0 = –4, А11 = (–1)1+1 (–4) = –4
= –4, А11 = (–1)1+1 (–4) = –4 = –21, А12 = (–1)1+2 ×(–1) = 21
= –21, А12 = (–1)1+2 ×(–1) = 21 = -1, А13 = (–1)1+3 ×1 = –1
= -1, А13 = (–1)1+3 ×1 = –1 = –2, А21 = (–1)2+1× (–2) = 2
= –2, А21 = (–1)2+1× (–2) = 2 =–13, А22 = (–1)2+2 × (–13) = –13
=–13, А22 = (–1)2+2 × (–13) = –13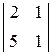 = –3, А23 = (–1)2+3 × (–3) = 3
= –3, А23 = (–1)2+3 × (–3) = 3 = 4, А31 = (–1)3+1× 4 = 4
= 4, А31 = (–1)3+1× 4 = 4 = 11, А32 = (–1)3+2 × 11 = –11
= 11, А32 = (–1)3+2 × 11 = –11 = 1, А33 = (–1)3+3 × 1 = 1
= 1, А33 = (–1)3+3 × 1 = 1 .
.
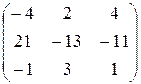 .
.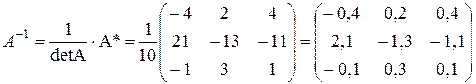 .
.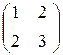 . 33.
. 33.  . 34.
. 34.  .
. . 36.
. 36.  . 37.
. 37.  .
.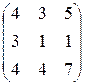 . 39.
. 39.  . 40.
. 40.  .
. . 42.
. 42. 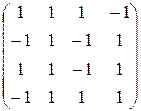 . 43.
. 43.  .
. .
.
 .
. А ~
А ~ 
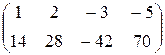 . 54.
. 54.  .
.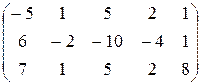 . 56.
. 56.  .
.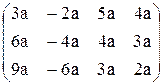 . 58.
. 58.  .
. а11х1 + а12х2 + … + а1nxn = b1
а11х1 + а12х2 + … + а1nxn = b1 .
.
 – матрица неизвестных;
– матрица неизвестных; – матрица свободных членов системы (1).
– матрица свободных членов системы (1). 60.
60. 
 62.
62. 
 . 64.
. 64.  .
. ,
, ;
; ;
; ;
;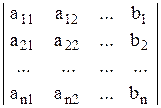 ;
; 2х1 + 3х2 + 4х3 = 15
2х1 + 3х2 + 4х3 = 15 = 44 ¹ 0
= 44 ¹ 0 = 0;
= 0; = 44;
= 44; = 132.
= 132. ;
;  ;
;  .
. . 66.
. 66.  .
. . 68.
. 68.  .
. . 70.
. 70. 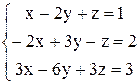 .
. . 72.
. 72. 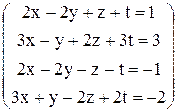 .
. . 74.
. 74.  .
. 3х1 + 2х2 + х3 = 17
3х1 + 2х2 + х3 = 17 .
. .
.
 и сложения ее с третьей строкой матрица А примет треугольный вид. Однако, чтобы упростить вычисления, можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим:
и сложения ее с третьей строкой матрица А примет треугольный вид. Однако, чтобы упростить вычисления, можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим: .
. .
. х1 + 4х2 - 3х3 = 9
х1 + 4х2 - 3х3 = 9 Найденное значение х3 = 1 подставим во второе уравнение системы, из которого х2 = 2х3 = 2 × 1 = 2.
Найденное значение х3 = 1 подставим во второе уравнение системы, из которого х2 = 2х3 = 2 × 1 = 2. 3 × 4 + 2 × 2 + 1 = 17 верно
3 × 4 + 2 × 2 + 1 = 17 верно . 76.
. 76.  .
.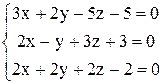 . 78.
. 78. 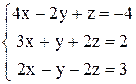 .
. . 80.
. 80.  .
. . 82.
. 82.  .
. . 84.
. 84.  .
.

 /
/

 . 86.
. 86.  .
. . 88.
. 88.  .
. . 90.
. 90. 
 ; 2.
; 2.  ; 3. 49;
; 3. 49; , ВА =
, ВА =  ; 5.
; 5. 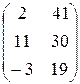 ; 6.
; 6.  ; 7. 7;
; 7. 7; ; 9.
; 9.  ; 10.
; 10.  ;
; ; 12. ( АВ)·С=А·(ВС)=
; 12. ( АВ)·С=А·(ВС)=  ;
; , А·С·В не существует, В·А·С не существует, В·С·А =
, А·С·В не существует, В·А·С не существует, В·С·А =  , С·А·В =
, С·А·В =  , С·В·А не существует; 14. –25; 15. 14; 16. –36; 17. –1; 18. –20; 19. 5; 20. –3; 21. 6; 22. 16; 23. –360; 24. 117; 25. 234; 26. 0; 27. 21; 28. –230; 29. –222; 30. –322; 31. 57; 32.
, С·В·А не существует; 14. –25; 15. 14; 16. –36; 17. –1; 18. –20; 19. 5; 20. –3; 21. 6; 22. 16; 23. –360; 24. 117; 25. 234; 26. 0; 27. 21; 28. –230; 29. –222; 30. –322; 31. 57; 32.  ;
; ; 34.
; 34.  ; 35.
; 35.  ; 36.
; 36.  ;
; ; 38.
; 38.  ; 39.
; 39.  ;
; ; 41.
; 41.  ;
; ; 43.
; 43.  ;
; ; 45.
; 45.  ; 46.
; 46.  ;
; ; 48.
; 48.  ; 49.
; 49.  ; 50.
; 50. 
 ; 52.
; 52.  ; 53. 2; 54. 2; 55. 3; 56. 4; 57. 2;
; 53. 2; 54. 2; 55. 3; 56. 4; 57. 2; ;
; (7 – 5с; с;
(7 – 5с; с; 


