Алгоритм метода Жордана-Гаусса

Элементы а₁₁; а₂₂;…; а_nn главной диагонали основной матрицы А системы (1) поочередно на каждом этапе решения задачи будут являться разрешающими элементами, а строки и столбцы, на пересечении которых они стоят, – разрешающими.

1. Выбрать разрешающий элемент и разделить на него разрешающую строку.

1. В разрешающем столбце записать нули вместо всех элементов, кроме разрешающего.

2. Остальные элементы расширенной матрицы системы пересчитать по правилу прямоугольника.

 

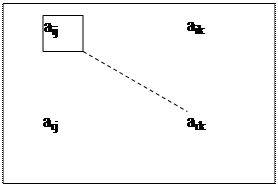
Правило прямоугольника

Пусть в матрице А системы а_ij – разрешающий элемент, а пересчитываемый элемент а_rk, тогда можно рассмотреть прямоугольник,

 

где разрешающий и искомый элементы лежат на одной его диагонали, называемой главной. Новое значение а'_rk пересчитываемого элемента а_rk вычисляется по формуле

а'_{rk =}

т. е. умножаем элементы главной диагонали прямоугольника, вычитаем произведение элементов другой его диагонали и результат делим на разрешающий элемент.

Аналогично пересчитывается столбец свободных членов

в^'_{r /}

Пример. Решить систему уравнений, используя алгоритм Жордана- Гаусса.

Решение. Запишем расширенную матрицу системы в виде таблицы и воспользуемся алгоритмом Жордана-Гаусса.

№ табл.	х1	х2	х3	вi
1.	-3	-5	-6 -3	-16
2.		-5/2 -11/2	-3 -4	5/2 17/2 -21
3.			-13/11 -39/11 8/11	15/11 17/11 78/11
4.				-3

Таблица № 4 задает систему уравнений, равносильную данной

откуда x₁ = 1; x₂ = –3; x₃ = 2.

Решить системы уравнений методом Жордана-Гаусса.

85. . 86. .

87. . 88. .

89. . 90.

 

Системы m линейных уравнений с n неизвестными

 

Понятие совместности системы уравнений

Рассмотрим систему m линейных уравнений с n неизвестными

а₁₁х₁ + а₁₂х₂ + … + а_1nx_n = b₁

а₂₁х₁ + а₂₂х₂ + … + а_2nx_n = b₂ (2)

……………………………….

а_m1х₁ + а_m2х₂ + … + а_mnx_n = b_m

Определение. Система уравнений называется совместной, если она имеет хотя бы одно решение, если же система не имеет ни одного решения, то она называется несовместной.

Определение. Совместная система называется определенной, если она имеет только одно решение, и неопределенной, если она имеет больше одного решения.

Теорема Кронекера-Капелли (критерий совместности системы уравнений).

Система m линейных уравнений с n неизвестными совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы, r(A) = r (В) = r, где r называется рангом системы, причем:

1. если r = n, то система имеет единственное решение, т. е. определена;

2. если r < n, то система имеет бесконечное множество решений, т. е. система не определена.