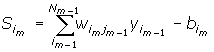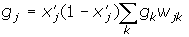Нейромережа зворотного поширення похибки (Back Propagation)

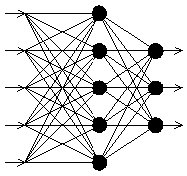
Архітектура FeedForward BackPropagation була розроблена на початку 1970-х років декількома незалежними авторами: Вербор (Werbor); Паркер (Parker); Румельгарт (Rumelhart), Хінтон (Hinton) та Вільямс (Williams). На даний час, парадигма ВackРropagation найбільш популярна, ефективна та легка модель навчання для складних, багатошарових мереж. Вона використовується у різних типах застосувань і породила великий клас нейромереж з різними структурами та методами навчання.

Типова мережа ВackРropagation має вхідний прошарок, вихідний прошарок та принаймні один прихований прошарок. Теоретично, обмежень відносно числа прихованих прошарків не існує, але практично застосовують один або два (рис. 3).

Рис. 3. Багатошаровий перцептрон

Нейрони організовані в пошарову структуру з прямою передачею сигналу. Кожний нейрон мережі продукує зважену суму своїх входів, пропускає цю величину через передатну функцію і видає вихідне значення. Мережа може моделювати функцію практично будь якої складності, причому число прошарків і число нейронів у кожному прошарку визначають складність функції. Визначення числа проміжних прошарків і числа нейронів в них є важливим при моделюванні мережі. Більшість дослідників та інженерів, застосовуючи архітектуру до визначених проблем використовують загальні правила, зокрема:

1. Кількість входів та виходів мережі визначаються кількістю вхідних та вихідних параметрів досліджуваного об'єкту, явища, процесу, тощо. На відміну від зовнішніх прошарків, число нейронів прихованого прошарку n _прих обирається емпіричним шляхом. В більшості випадків достатня кількість нейронів становить n _прих £ n _вх + n _вих, де n _вх, n _вих - кількість нейронів у вхідному і, відповідно, у вихідному прошарках.
2. Якщо складність у відношенні між отриманими та бажаними даними на виході збільшується, кількість нейронів прихованого прошарку повинна також збільшитись.
3. Якщо процес, що моделюється, може розділятись на багато етапів, потрібен додатковий прихований прошарок (прошарки). Якщо процес не розділяється на етапи, тоді додаткові прошарки можуть допустити перезапам'ятовування і, відповідно, невірне загальне рішення.

Після того, як визначено число прошарків і число нейронів в кожному з них, потрібно знайти значення для синаптичних ваг і порогів мережі, які спроможні мінімізувати похибку спродукованого результату. Саме для цього існують алгоритми навчання, де відбувається підгонка моделі мережі до наявних навчальних даних. Похибка для конкретної моделі мережі визначається шляхом проходження через мережу всіх навчальних прикладів і порівняння спродукованих вихідних значень з бажаними значеннями. Множина похибок створює функцію похибок, значення якої можна розглядати, як похибку мережі. В якості функції похибок найчастіше використовують суму квадратів похибок.

Для кращого розуміння алгоритму навчання мережі Back Propagation потрібно роз'яснити поняття поверхні станів. Кожному значенню синаптичних ваг і порогів мережі (вільних параметрів моделі кількістю N) відповідає один вимір в багатовимірному просторі. N +1-ий вимір відповідає похибці мережі. Для різноманітних сполучень ваг відповідну похибку мережі можна зобразити точкою в N +1-вимірному просторі, всі ці точки утворюють деяку поверхню - поверхню станів. Мета навчання нейромережі полягає в знаходженні на багатовимірній поверхні найнижчої точки.

Поверхня станів має складну будову і досить неприємні властивості, зокрема, наявність локальних мінімумів (точки, найнижчі в своєму певному околі, але вищі від глобального мінімуму), пласкі ділянки, сідлові точки і довгі вузькі яри. Аналітичними засобами неможливо визначити розташування глобального мінімуму на поверхні станів, тому навчання нейромережі по суті полягає в дослідженні цієї поверхні. Відштовхуючись від початкової конфігурації ваг і порогів (від випадково обраної точки на поверхні), алгоритм навчання поступово відшукує глобальний мінімум. Обчислюється вектор градієнту поверхні похибок, який вказує напрямок найкоротшого спуску по поверхні з заданої точки. Якщо трошки просунутись по ньому, похибка зменшиться. Зрештою алгоритм зупиняється в нижній точці, що може виявитись лише локальним мінімумом (в ідеальному випадку - глобальним мінімумом). Складність тут полягає у виборі довжини кроків. При великій довжині кроку збіжність буде швидшою, але є небезпека перестрибнути рішення, або піти в неправильному напрямку. При маленькому кроці, правильний напрямок буде виявлений, але зростає кількість ітерацій. На практиці розмір кроку береться пропорційним крутизні схилу з деякою константою - швидкістю навчання. Правильний вибір швидкості навчання залежить від конкретної задачі і здійснюється дослідним шляхом. Ця константа може також залежати від часу, зменшуючись по мірі просування алгоритму.

Алгоритм діє ітеративне, його кроки називаються епохами. На кожній епосі на вхід мережі по черзі подаються всі навчальні приклади, вихідні значення мережі порівнюються з бажаними значеннями і обчислюється похибка. Значення похибки, а також градієнту поверхні станів використовують для корекції ваг, і дії повторюються. Процес навчання припиняється або коли пройдена визначена кількість епох, або коли похибка досягає визначеного рівня малості, або коли похибка перестає зменшуватись (користувач переважно сам вибирає потрібний критерій останову).

Алгоритм навчання мережі

1. Ініціалізація мережі: вагові коефіцієнти і зсуви мережі приймають малі випадкові значення.
2. Визначення елемента навчальної множини: (вхід - вихід). Входи (x ₁, x ₂... x_N), повинні розрізнятися для всіх прикладів навчальної множини.
3. Обчислення вихідного сигналу:

y_im = f (S_jm)

i_m =1, 2,..., N_m, m =1, 2,..., L

де S - вихід суматора, w - вага зв'язку, y - вихід нейрона, b - зсув, i - номер нейрона, N - число нейронів у прошарку, m - номер прошарку, L - число прошарків, f - передатна функція.

1. Налаштування синаптичних ваг:

w_ij (t +1)= w_ij (t)+ rg_jx'_і

де w_ij - вага від нейрона i або від елемента вхідного сигналу i до нейрона j у момент часу t, x_i ' - вихід нейрона i, r - швидкість навчання, g_j - значення похибки для нейрона j.

Якщо нейрон з номером j належить останньому прошарку, тоді

g_j = y_j (1- y_j)(d_j - y_j)

де d_j - бажаний вихід нейрона j, y_j - поточний вихід нейрона j.

Якщо нейрон з номером j належить одному з прошарків з першого по передостанній, тоді

де k пробігає всі нейрони прошарку з номером на одиницю більше, ніж у того, котрому належить нейрон j.

Зовнішні зсуви нейронів b налаштовуються аналогічним образом.

Тип вхідних сигналів: цілі чи дійсні.

Тип вихідних сигналів: дійсні з інтервалу, заданого передатною функцією нейронів.

Тип передатної функції: сигмоїдальна. В нейронних мережах застосовуються кілька варіантів сигмоїдальних передатних функцій.

Функція Ферми (експонентна сигмоїда):

де s - вихід суматора нейрона, a - деякий параметр.

Раціональна сигмоїда:

Гіперболічний тангенс:

Згадані функції відносяться до однопараметричних. Значення функції залежить від аргументу й одного параметра. Також використовуються багатопараметричні передатні функції, наприклад:

Сигмоїдальні функції є монотонно зростаючими і мають відмінні від нуля похідні по всій області визначення. Ці характеристики забезпечують правильне функціонування і навчання мережі.

Області застосування. Розпізнавання образів, класифікація, прогнозування.

Недоліки. Багатокритеріальна задача оптимізації в методі зворотного поширення розглядається як набір однокритеріальних задач - на кожній ітерації відбуваються зміни значень параметрів мережі, що покращують роботу лише з одним прикладом навчальної вибірки. Такий підхід істотно зменшує швидкість навчання.

Переваги. Зворотне поширення - ефективний та популярний алгоритм навчання багатошарових нейронних мереж, з його допомогою вирішуються численні практичні задачі.

Модифікації. Модифікації алгоритму зворотного поширення зв'язані з використанням різних функцій похибки, різних процедур визначення напрямку і величини кроку.

Delta Bar Delta

Delta bar Delta була розроблена Робертом Джекобсом (Robert Jacobs), для покращення оцінки навчання стандартних мереж FeedForward і є модифікацією мережі BackPropagation.

Процедура BackPropagation базується на підході найкрутішого спуску, який мінімізує похибку передбачення мережі під час процесу змінювання синаптичних ваг. Стандартні оцінки навчання застосовуються на базисі "прошарок за прошарком" і значення моменту призначаються глобально. Моментом вважається фактор, що використовується для згладжування оцінки навчання. Момент додається до стандартної зміни ваги і є пропорційним до попередньої зміни ваги. Хоча цей метод є успішним у вирішенні багатьох задач, збіжність процедури занадто повільна для використання.

Парадигма Delta bar Delta має "неформальний" підхід до навчання штучних мереж, при якому кожна вага має свій власний самоадаптований фактор навчання і минулі значення похибки використовуються для обчислення майбутніх значень. Знання ймовірних похибок дозволяє мережі робити інтелектуальні кроки при змінюванні ваг, але процес ускладнюється тим, що кожна вага може мати зовсім різний вплив на загальну похибку. Джекобс запропонував поняття "здорового глузду", коли кожна вага з'єднання мережі повинна мати власну оцінку навчання, а розмір кроку, що призначений до одної ваги з'єднання не застосовується для всіх ваг у прошарку.

Оцінка навчання ваги з'єднання змінюється на основі інформації про біжучу похибку, знайденої із стандартної ВackРropagation. Якщо локальна похибка має однаковий знак для декількох послідовних часових кроків, оцінка навчання для цього з'єднання лінійно збільшується. Якщо локальна похибка часто змінює знак, оцінка навчання зменшується геометрично і це гарантує, що оцінки навчання з'єднання будуть завжди додатними. Оцінкам навчання дозволено змінюватись в часі. Призначення оцінки навчання до кожного з'єднання, дозвіл цій оцінці навчання неперервне змінюватись з часом обумовлюють зменшення часу збіжності.

З дозволом різних оцінок навчання для кожної ваги з'єднання у мережі, пошук найкрутішого спуску може не виконуватись. Замість цього, ваги з'єднань змінюються на основі часткових похідних похибки відносно самої ваги і оцінці "кривини поверхні похибки" поблизу біжучої точки значення ваги. Зміни ваг відповідають обмеженню місцевості і вимагають інформацію від нейронів, з якими вони з'єднані.

Переваги. Парадигма Delta Bar Delta є спробою прискорити процес збіжності алгоритму зворотного поширення за рахунок використання додаткової інформації про зміну параметрів і ваг під час навчання.

Недоліки:

• Навіть невелике лінійне збільшення коефіцієнта може привести до значного росту швидкості навчання, що викликає стрибки в просторі ваг.
• Геометричне зменшення коефіцієнта іноді виявляється не досить швидким.

Extended Delta Bar Delta

Елі Мінаї (Ali Minai) та Рон Вільямс (Ron Williams) розробили алгоритм Extended Delta bar Delta, як природній наслідок роботи Джекобса. В алгоритм вбудовується пам'ять з особливістю відновлення. Після кожного представлення навчальних даних епохи, оцінюється накопичена похибка. Якщо похибка є меншою за попередню мінімальну похибку, ваги зберігаються у пам'яті, як найкращі на цей час. Параметр допуску керує фазою відновлення. У випадку, коли біжуча похибка перевищує мінімальну попередню похибку, модифіковану параметром допуску, всі значення ваг з'єднань стохастичне повертаються до збереженої у пам'яті найкращої множини ваг.

Скерований випадковий пошук

Мережа скерованого випадкового пошуку (Directed Random Search), використовує стандартну архітектуру FeedForward, яка не базується на алгоритмі BackProragation і коректує ваги випадковим чином. Для забезпечення порядку в такому процесі, до випадкового кроку додається компонента напрямку, яка гарантує скерування ваг до попередньо успішного напрямку пошуку. Вплив на всі нейрони здійснюється окремо.

Для збереження ваг всередині компактної області, де алгоритм працює добре, встановлюють верхню межу величини ваги. Встановлюючи межі ваг великими, мережа може продовжувати працювати, оскільки справжній глобальний оптимум лишається невідомим. Іншою особливістю правила навчання є початкова відмінність у випадковому розподілі ваг. У більшості комерційних пакетів існує рекомендоване розробником число для параметра початкової відмінності.

Парадигма випадкового пошуку має декілька важливих рис. Вона є швидкою та легкою у використанні, найкращі результати отримують, коли початкові ваги знаходяться близько до найкращих ваг. Швидкою парадигма є завдяки тому, що для проміжних нейронів похибки не обчислюються, а обчислюється лише вихідна похибка. Алгоритм надає ефект лише в малій мережі, оскільки при збільшенні числа з'єднань, процес навчання стає довгим та важким.

Існує чотири ключові компоненти мережі з випадковим пошуком. Це є випадковий крок, крок реверсування, скерована компонента та самокорегуюча відмінність.

Випадковий крок. До кожної ваги додається випадкова величина. Вся навчальна множина пропускається через мережу, створюючи "похибку передбачення". Якщо нова загальна похибка навчальної множини є меншою за попередню найкращу похибку передбачення, біжучі значення ваг, які включають випадковий крок стають новою множиною "найкращих" ваг. Біжуча похибка передбачення зберігається як нова, найкраща похибка передбачення.

Крок реверсування. Якщо результати випадкового кроку є гіршими за попередні найкращі, випадкова величина віднімається від початкового значення ваги. Це створює множину ваг, які знаходяться в протилежному напрямку до попереднього випадкового кроку. Якщо загальна "похибка передбачення" є меншою за попередню найкращу похибку, біжучі значення ваг та біжуча похибка передбачення зберігаються як найкращі. Якщо і прямий і зворотній кроки не покращують результат, до найкращих ваг додається повністю нова множина випадкових значень і процес починається спочатку.

Скерована компонента. Для збіжності мережі створюється множина скерованих компонент, отриманих по результатах прямого та зворотного кроків. Скеровані компоненти, що відображають ланку успіхів або невдач попередніх випадкових кроків, додаються до випадкових компонент на кожному кроці процедури і забезпечують елемент "здорового глузду" до пошуку. Доведено, що додавання скерованих компонент забезпечує різке підвищення ефективності алгоритму.

Самокорегуюча відмінність. Визначається параметр початкової відмінності для керування початковим розміром випадкових кроків, що додається до ваг. Адаптивний механізм змінює параметр відмінності, який базується на біжучій оцінці успіху або невдачі. Правило навчання припускає, що біжучий розмір кроків для ваг у правильному напрямку збільшується для випадку декількох послідовних успіхів. Навпаки, якщо воно виявляє декілька послідовних невдач, відмінність зменшується для зменшення розміру кроку.

Переваги. Для малих та середніх нейромереж, скерований випадковий пошук надає добрі результати за короткий час. Навчання є автоматичним, вимагає невеликої взаємодії з користувачем.

Недоліки. Кількість ваг з'єднань накладає практичні обмеження на розмір задачі. Якщо мережа має більше ніж 200 ваг з'єднань, скерований випадковий пошук може вимагати збільшення часу навчання, але продукувати прийнятні рішення.