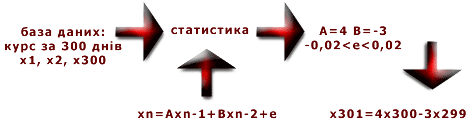Призначення аналітичних технологій

Аналітичні технології потрібні в першу чергу людям, що приймають важливі рішення - керівникам, аналітикам, експертам, консультантам. Дохід компанії у великому ступені визначається якістю цих рішень - точністю прогнозів, оптимальністю обраних стратегій.

• Прогнозування:
• курсів валют;
• цін на сировину;
• попиту;
• доходу компанії;
• рівня безробіття;
• числа страхових випадків.
• Оптимізація:
• розкладів;
• маршрутів;
• плану закупівель;
• плану інвестицій;
• стратегії розвитку.

Як правило, для реальних задач бізнесу й виробництва не існує чітких алгоритмів рішення. Зазвичай керівники й експерти вирішували такі задачі тільки на основі особистого досвіду. Часто класичні методики виявляються малоефективними в багатьох практичних задачах. Це пояснюється тим, що неможливо досить точно описати реальність за допомогою невеликого числа параметрів моделі, або розрахунок моделі займає занадто багато часу та обчислювальних ресурсів, а за допомогою аналітичних технологій будуються системи, що дозволяють істотно підвищити ефективність рішень.

Традиційні технології

Детерміновані технології

Аналітичні технології типу теореми Піфагора використовуються людиною вже багато століть. За цей час була створена величезна кількість формул, теорем і алгоритмів для рішення класичних задач - визначення об'ємів, рішення систем лінійних рівнянь, пошуку коренів багаточленів. Розроблено складні й ефективні методи для рішення задач оптимального керування, рішення диференційних рівнянь і т.д. Всі ці методи діють по однієї і тій же схемі.

Для застосування алгоритму необхідно, щоб дана задача цілком описувалася визначеною детермінованою моделлю (деяким набором відомих функцій і параметрів). У такому випадку алгоритм дає точну відповідь. Наприклад, для застосування теореми Піфагора потрібно перевірити, що трикутник - прямокутний.

Імовірнісні технології

На практиці часто зустрічаються задачі, пов'язані зі спостереженням випадкових величин - наприклад, задача прогнозування курсу акцій. Для подібних задач не можна побудувати детерміновані моделі, тому застосовується принципово інший, імовірнісний підхід.

Параметри імовірнісних моделей - це розподіли випадкових величин, їхні середні значення, дисперсії і т.д. Як правило, ці параметри заздалегідь невідомі, а для їхньої оцінки використовуються статистичні методи, що застосовуються до вибірок спостережених значень (історичних даних).

Такого роду методи припускають, що відомо деяка імовірнісна модель задачі. Наприклад, у задачі прогнозування курсу можна припустити, що завтрашній курс акцій залежить тільки від курсу за останні 2 дні (авторегресійна модель). Якщо це вірно, то спостереження курсу протягом декількох місяців дозволяють досить точно оцінити коефіцієнти цієї залежності і прогнозувати курс у майбутньому.

Приклади реальних задач