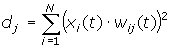Нейронна мережа вищого порядку або функціонально-пов'язана нейронна мережа

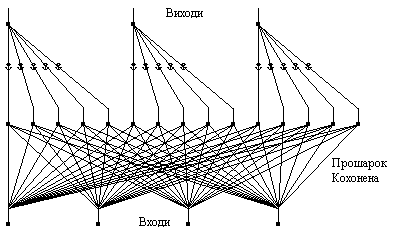
Функціонально-пов'язані мережі були розроблені Йох-Хан Пао (Yoh-Han Pao) і детально описані в його книзі "Адаптивне розпізнавання образів та нейронні мережі" (Adaptive Pattern Recognition and Neural Networks). Нейромережа розширює стандартну архітектуру FeedForward BackPropagation модифікацією вузлів на вхідному прошарку. Входи комбінуються зрозумілим математичним шляхом за допомогою функцій вищого порядку, таких як квадрати, куби або синуси і розширюють сприйняття мережею заданої проблеми. Із назв цих функцій, вищого порядку або функціонально пов'язаних входів і випливає назва нейромереж.

Існує два основних способи додавання вхідних вузлів. В першому, у модель можуть додаватись перехресні добутки вхідних елементів, це називається вхідним добутком або тензорною моделлю, де кожна компонента вхідного образу перемножується зі всіма компонентами вхідного вектора. Наприклад, для мережі ВackРropagation з трьома входами (A, B і C), перехресними добутками будуть AA, BB, CC, AB, AC та BC (елементи другого порядку). Також можуть додаватись елементи третього порядку, такі як ABC.

Другим методом для додавання вхідних вузлів є функціональне розширення базових входів. У випадку моделі з входами A, B і C, її можна перетворити у модель нейронної мережі вищого порядку зі входами: A, B, C, SIN (A), COS (B), LOG (C), MAX (A,B,C) та ін. Повний ефект повинна забезпечити мережа з об'єднанням моделі тензорного та функціонального розширення.

Ніякої нової інформації не додається, але розширене представлення входів робить мережу простішою для навчання. Існують обмеження для цієї моделі. Для перетворення початкових входів необхідна обробка більшої кількості вхідних вузлів, що впливає на швидкодію мережі, тому при розширенні входів має бути враховане поєднання точного рішення та порівняно невеликого часу навчання.

Мережа Кохонена

Мережа розроблена Тойво Кохоненом на початку 1980-х рр. і принципово відрізняється від розглянутих вище мереж, оскільки використовує неконтрольоване навчання і навчальна множина складається лише із значень вхідних змінних.

Мережа розпізнає кластери в навчальних даних і розподіляє дані до відповідних кластерів. Якщо в наступному мережа зустрічається з набором даних, несхожим ні з одним із відомих зразків, вона відносить його до нового кластеру. Якщо в даних містяться мітки класів, то мережа спроможна вирішувати задачі класифікації. Мережі Кохонена можна використовувати і в задачах, де класи відомі - перевага буде у спроможності мережі виявляти подібність між різноманітними класами.

Мережа Кохонена має всього два прошарки: вхідний і вихідний, що називають самоорганізованою картою. Елементи карти розташовуються в деякому просторі - як правило двовимірному.

Рис. 4. Мережа Кохонена

Мережа Кохонена навчається методом послідовних наближень. Починаючи з випадковим чином обраного вихідного розташування центрів, алгоритм поступово покращується для кластеризації навчальних даних.

Проте, алгоритм може працювати і на іншому рівні. В результаті ітеративної процедури навчання мережа організовується таким чином, що елементи, які відповідають центрам, розташованим близько один від одного в просторі входів, будуть розташовані близько один від одного і на топологічній карті. Топологічний прошарок мережі можна уявити як двовимірну штахету, яку потрібно так відобразити в N -вимірний простір входів, щоб по можливості зберегти вихідну структуру даних. Звісно ж, при будь-якій спробі відтворити N -вимірний простір на площині буде загублено багато деталей, але такий прийом дозволяє користувачу візуалізувати дані, що неможливо зрозуміти іншим засобом.

Основний ітераційний алгоритм Кохонена послідовно проходить ряд епох, на кожній епосі опрацьовується один навчальний приклад. Вхідні сигнали - вектори дійсних чисел - послідовно пред'являються мережі. Бажані вихідні сигнали не визначаються. Після пред'явлення достатнього числа вхідних векторів, синаптичні ваги мережі визначають кластери. Крім того, ваги організуються так, що топологічне близькі вузли чуттєві до схожих вхідних сигналів.

Для реалізації алгоритму необхідно визначити міру сусідства нейронів (окіл нейрона-переможця). На мал. 6 показані зони топологічного сусідства нейронів на карті ознак у різні моменти часу. NE_j (t) - множина нейронів, що вважаються сусідами нейрона j у момент часу t. Зони сусідства зменшуються з часом.

Рис. 5. Зони топологічного сусідства на карті ознак у різні моменти часу

Алгоритм функціонування мережі Кохонена:

1. Ініціалізація мережі. Ваговим коефіцієнтам мережі надаються малі випадкові значення. Початкова зона сусідства показана на рис. 5.
2. Пред'явлення мережі нового вхідного сигналу.
3. Обчислення відстані до всіх нейронів мережі:

Відстані d_j від вхідного сигналу до кожного нейрона j визначаються за формулою:

де x_i - i-ий елемент вхідного сигналу в момент часу t, w_ij (t) - вага зв'язку від i-го елемента вхідного сигналу до нейрона j у момент часу t.

1. Вибір нейрона з найменшою відстанню:

Вибирається нейрон-переможець j^*, для якого відстань d_j найменше.

1. Налаштування ваг нейрона j^* і його сусідів:

Робиться налаштування ваг для нейрона j^* і всіх нейронів з його околу NE. Нові значення ваг:

w_ij (t +1)= w_ij (t)+ r (t)(x_i (t)- w_ij (t))

де r (t) - швидкість навчання, що зменшується з часом (додатне число, менше одиниці).

1. Повернення до кроку 2.

В алгоритмі використовується коефіцієнт швидкості навчання, який поступово зменшується, для тонкішої корекції на новій епосі. В результаті позиція центру встановлюється в певній позиції, яка задовільним чином кластеризує приклади, для яких даний нейрон є переможцем.

Властивість топологічної впорядкованості досягається в алгоритмі за допомогою використання поняття околу. Окіл - це декілька нейронів, що оточують нейрон-переможець. Відповідно до швидкості навчання, розмір околу поступово зменшується, так, що спочатку до нього належить досить велике число нейронів (можливо вся карта), на самих останніх етапах окіл стає нульовим і складається лише з нейрона-переможця. В алгоритмі навчання корекція застосовується не тільки до нейрона-переможця, але і до всіх нейронів з його поточного околу. В результаті такої зміни околу, початкові доволі великі ділянки мережі мігрують в бік навчальних прикладів. Мережа формує грубу структуру топологічного порядку, при якій схожі приклади активують групи нейронів, що близько знаходяться на топологічній карті. З кожною новою епохою швидкість навчання і розмір околу зменшуються, тим самим всередині ділянок карти виявляються більш тонкі розходження, що зрештою призводить до точнішого налаштування кожного нейрона. Часто навчання зумисне розбивають на дві фази: більш коротку, з великою швидкістю навчання і великих околів, і більш тривалу з малою швидкістю навчання і нульовими або майже нульовими околами.

Після того, як мережа навчена розпізнаванню структури даних, її можна використовувати як засіб візуалізації при аналізі даних.

Області застосування. Кластерний аналіз, розпізнавання образів, класифікація.

Недоліки. Мережа може бути використана для кластерного аналізу тільки в тому випадку, якщо заздалегідь відоме число кластерів.

Переваги. Мережа Кохонена здатна функціонувати в умовах перешкод, тому що число кластерів фіксоване, ваги модифікуються повільно, налаштування ваг закінчується після навчання.

Модифікації. Одна з модифікацій полягає в тому, що до мережі Кохонена додається мережа MAXNET, що визначає нейрон з найменшою відстанню до вхідного сигналу.

Квантування навчального вектора (Learning VectorQuantization)

Мережа запропонована Тойво Кохоненом у середині 80-х рр., набагато пізніше за його початкову роботу по самоорганізованим картам. Мережа базується на прошарку Кохонена, який здатний до сортування прикладів у відповідні кластери і використовується як для проблем класифікації, так і для кластеризації зображень.

Мережа містить вхідний прошарок, самоорганізовану карту Кохонена та вихідний прошарок. Приклад мережі зображений на рис. 6. Вихідний прошарок має стільки нейронів, скільки є відмінних категорій або класів. Карта Кохонена має ряд нейронів, згрупованих для кожного з цих класів. Кількість елементів обробки на один клас залежить від складності відношення "вхід-вихід". Звичайно, кожен клас буде мати однакову кількість елементів по всьому прошарку. Прошарок Кохонена навчається класифікації за допомогою навчальної множини. Мережа використовує правила контрольованого навчання. Вхідний прошарок повинен містити лише один нейрон для кожного окремого вхідного параметра.

Квантування навчального вектора класифікує вхідні дані у визначені групування, тобто відображає n -вимірний простір у m -вимірний простір (бере n входів і створює m виходів). Карти зберігають відношення між близькими сусідами у навчальній множині так, що вхідні образи, які не були попередньо вивчені, будуть розподілені за категоріями їх найближчих сусідів у навчальних даних.

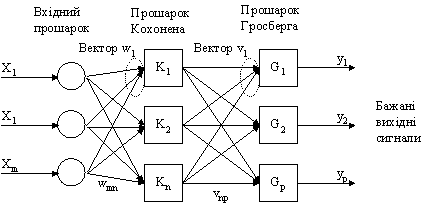
Рис. 6. Приклад мережі з квантуванням навчального вектора.

У режимі навчання, контрольована мережа використовує прошарок Кохонена, де обчислюється відстань від навчального вектора до кожного нейрону і найближчий нейрон оголошується переможцем. Існує лише один переможець на весь прошарок. Переможцю дозволено збуджувати лише один вихідний нейрон, оголошуючи клас або кластер до якого належить вхідний вектор. Якщо нейрон-переможець знаходиться у очікуваному класі навчального вектора, його ваги підсилюються у напрямку навчального вектора. Якщо нейрон-переможець не є у класі навчального вектора, ваги з'єднань зменшуються. Ця остання операція згадується як відштовхування (repulsion). Під час навчання окремі нейрони, що приписані до часткового класу мігрують до області, пов'язаної з їх специфічним класом.

Під час режиму функціонування, обчислюється відстань від вхідного вектора до кожного нейрону і знову найближчий нейрон оголошується переможцем. Це в свою чергу генерує один вихід, визначаючи частковий клас, знайдений мережею.

Недоліки. Для складних проблем класифікації з подібними вхідними прикладами, мережа вимагає великої карти Кохонена з багатьма нейронами на клас. Це вибірково може бути подолано вибором доцільних навчальних прикладів або розширенням вхідного прошарку.

Мережа квантування навчального вектора страждає від дефекту, що деякі нейрони мають тенденцію до перемоги занадто часто, тобто налаштовують свої ваги дуже швидко, а інші постійно залишаються незадіяними. Це часто трапляється, коли їх ваги мають значення далекі від навчальних прикладів. Щоб пом'якшити цю проблему, нейрон, який перемагає занадто часто штрафується, тобто зменшуються ваги його зв'язків з кожним вхідним нейроном. Це зменшення ваг є пропорційним до різниці між частотою перемог нейрону та частотою перемог середнього нейрону.

Переваги. Алгоритм граничної корекції використовується для вдосконалення рішення навіть коли було знайдено відносно добре рішення. Алгоритм спроможний діяти, коли нейрон-переможець знаходиться у неправильному класі, а другий найкращий нейрон у правильному класі. Навчальний вектор повинен бути близько від середньої точки простору, що з'єднує ці два нейрони. Неправильний нейрон-переможець зміщується з навчального вектора, а нейрон з іншого місця посувається до навчального вектора. Ця процедура робить чіткішою межу між областями, де можлива невірна класифікація.

На початку навчання бажано відключити відштовхування. Нейрон-переможець пересувається до навчального вектора лише тоді, коли навчальний вектор та нейрон-переможець знаходяться в одному класі. Це право вибору доцільне, коли нейрон повинен оминати область, яка має відмінний клас для досягнення необхідної області.

Мережа зустрічного поширення (CounterРropagation)

Роберт Хехт-Нільсен (Robert Hecht-Nielsen) розробив мережу СounterРropagation як засіб для поєднання неконтрольованого прошарку Кохонена із контрольованим вихідним прошарком. Мережа призначена для вирішення складних класифікацій, при мінімізації числа нейронів та часу навчання. Навчання для мережі СounterРropagation подібне до мережі з квантуванням навчального вектора.

Приклад мережі зображений на рис. 7. Односкерована мережа CounterPropagation має три прошарки: вхідний прошарок, самоорганізовану карту Кохонена та вихідний прошарок, що використовує правило "дельта" для зміни вхідних ваг з'єднань. Цей прошарок називають прошарком Гросберга.

Рис. 7. Мережа зустрічного поширення без зворотних зв'язків

Перша мережа СounterРropagation складалась із двоскерованого відображення між вхідним та вихідним прошарками. Дані надходять на вхідний прошарок для генерації класифікації на вихідному прошарку, вихідний прошарок по черзі приймає додатковий вхідний вектор та генерує вихідну класифікацію на вхідному прошарку мережі. Через такий зустрічно-поширений потік інформації випливає назва мережі. Багато розробників використовують односкерований варіант СounterРropagation, коли існує лише один шлях прямого поширення від вхідного до вихідного прошарку.

У мережі зустрічного поширення об'єднані два алгоритми: самоорганізована карта Кохонена і зірка Гросберга (Grossberg Outstar). Кожен елемент вхідного сигналу подається на всі нейрони прошарку Кохонена. Ваги зв'язків (w_mn) утворюють матрицю W. Кожен нейрон прошарку Кохонена з'єднаний зі всіма нейронами прошарку Гросберга. Ваги зв'язків (v_np) утворюють матрицю ваг V. Нейронні мережі, що поєднують різні нейропарадигми як будівельні блоки, більш близькі до мозку по архітектурі, ніж однорідні структури. Вважається, що в мозку саме каскадні з'єднання модулів різної спеціалізації дозволяють виконувати необхідні обчислення.

У процесі навчання мережі зустрічного поширення вхідні вектори асоціюються з відповідними вихідними векторами (двійковими або аналоговими). Після навчання мережа формує вихідні сигнали, що відповідають вхідним сигналам. Узагальнююча здатність мережі дає можливість одержувати правильний вихід, якщо вхідний вектор неповний чи спотворений.

Навчання мережі

Карта Кохонена класифікує вхідні вектори в групи схожих. В результаті самонавчання прошарок здобуває здатність розділяти несхожі вхідні вектори. Який саме нейрон буде активуватися при пред'явленні конкретного вхідного сигналу, заздалегідь важко передбачити.

При навчанні прошарку Кохонена на вхід подається вхідний вектор і обчислюються його скалярні добутки з векторами ваг всіх нейронів.

Скалярний добуток є мірою подібності між вхідним вектором і вектором ваг. Нейрон з максимальним значенням скалярного добутку з'являється "переможцем" і його ваги підсилюються (ваговий вектор наближається до вхідного).

w_н = w_c + r (x - w_c)

де w _н - нове значення ваги, що з'єднує вхідний компонент x з нейроном-переможцем, w _с - попереднє значення цієї ваги, r - коефіцієнт швидкості навчання, що спочатку звичайно дорівнює 0.7 і може поступово зменшуватися в процесі навчання. Це дозволяє робити великі початкові кроки для швидкого грубого навчання і менші кроки при підході до остаточної величини.

Кожна вага, зв'язана з нейроном-переможцем Кохонена, змінюється пропорційно різниці між його величиною і величиною входу, до якого він приєднаний. Напрямок зміни мінімізує різницю між вагою і відповідним елементом вхідного прошарку.

Навчальна множина може містити багато подібних між собою вхідних векторів, і мережа повинна бути навченою активувати один нейрон Кохонена для кожного з них. Ваги цього нейрона уявляють собою усереднення вхідних векторів, що його активують.

Виходи прошарку Кохонена подаються на входи нейронів прошарку Гросберга. Входи нейронів обчислюються як зважена сума виходів прошарку Кохонена. Кожна вага коректується лише в тому випадку, якщо вона з'єднана з нейроном Кохонена, який має ненульовий вихід. Величина корекції ваги пропорційна різниці між вагою і необхідним виходом нейрона Гросберга. Навчання прошарку Гросберга - це навчання "з вчителем", алгоритм використовує задані бажані виходи.

Функціонування мережі

У своїй найпростішій формі прошарок Кохонена функціонує за правилом "переможець отримує все". Для даного вхідного вектора один і тільки один нейрон Кохонена видає логічну одиницю, всі інші видають нуль.

Прошарок Гросберга функціонує в схожій манері. Його вихід є зваженою сумою виходів прошарку Кохонена.

Якщо прошарок Кохонена функціонує таким чином, що лише один вихід дорівнює одиниці, а інші дорівнюють нулю, то кожен нейрон прошарку Гросберга видає величину ваги, що зв'язує цей нейрон з єдиним нейроном Кохонена, чий вихід відмінний від нуля.

У повній моделі мережі зустрічного поширення є можливість одержувати вихідні сигнали по вхідним і навпаки. Цим двом діям відповідають пряме і зворотне поширення сигналів.

Області застосування. Розпізнавання образів, відновлення образів (асоціативна пам'ять), стиснення даних (із втратами).

Недоліки. Мережа не дає можливості будувати точні апроксимації (точні відображення). У цьому мережа значно уступає мережам зі зворотним поширенням похибки. До недоліків моделі також варто віднести слабкий теоретичний базис модифікацій мережі зустрічного поширення.

Переваги:

• Мережа зустрічного поширення проста. Вона дає можливість витягати статистичні властивості з множини вхідних сигналів. Кохонен довів, що для навченої мережі імовірність того, що випадково обраний вхідний вектор буде найближчим до будь-якого заданого вагового вектора, дорівнює 1/k, k - число нейронів Кохонена.
• Мережа швидко навчається. Час навчання в порівнянні зі зворотним поширенням може бути в 100 разів менше.
• По своїх можливостях будувати відображення мережа зустрічного поширення значно перевершує одношарові перцептрони.
• Мережа корисна для застосувань, у яких потрібно швидка початкова апроксимація.
• Мережа дає можливість будувати функцію і зворотну до неї, що знаходить застосування при рішенні практичних задач.

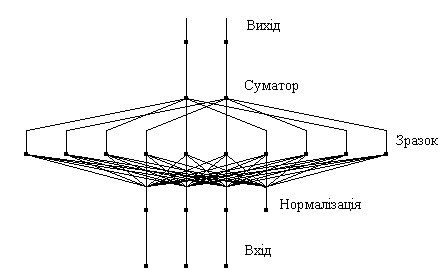
Модифікації. Мережі зустрічного поширення можуть розрізнятися способами визначення початкових значень синаптичних ваг.

Для підвищення ефективності навчання застосовується додавання шуму до вхідних векторів.

Ще один метод підвищення ефективності навчання - надання кожному нейрону "почуття справедливості". Якщо нейрон стає переможцем частіше, ніж 1/k (k - число нейронів Кохонена), то йому тимчасово збільшують поріг, даючи тим самим навчатися й іншим нейронам.

Крім "методу акредитації", при якому для кожного вхідного вектора активується лише один нейрон Кохонена, може бути використаний "метод інтерполяції", при використанні якого ціла група нейронів Кохонена, що мають найбільші виходи, може передавати свої вихідні сигнали в прошарок Гросберга. Цей метод підвищує точність відображень, реалізованих мережею.

Імовірнісна нейронна мережа

Імовірнісна нейронна мережа була розроблена Дональдом Спехтом (Donald Specht). Ця мережна архітектура була вперше представлена у двох статтях: "Імовірнісні нейронні мережі для класифікації" (Probabilistic Neural Networks for Classification) 1988, "Відображення або асоціативна пам'ять та імовірнісні нейронні мережі" (Mapping or Associative Memory and Probabilistic Neural Networks) 1990 р.

Виходи мережі можна інтерпретувати, як оцінки ймовірності належності елементу певному класу. Імовірнісна мережа вчиться оцінювати функцію густини ймовірності, її вихід розглядається як очікуване значення моделі в даній точці простору входів. Це значення пов'язане з густиною ймовірності спільного розподілу вхідних і вихідних даних.

Задача оцінки густини ймовірності відноситься до області байєсівської статистики. Звичайна статистика по заданій моделі показує, яка ймовірність того або іншого виходу (наприклад, на гральній кістці 6 очок буде випадати в середньому в одному випадку з шістьох). Байєсова статистика інтерпретує по іншому: правильність моделі оцінюється по наявних достовірних даних, тобто надає можливість оцінювати густину ймовірності розподілу параметрів моделі по наявних даних.

При рішенні задач класифікації можна оцінити густину ймовірності для кожного класу, порівняти між собою ймовірності приналежності до різних класів і обрати модель з параметрами, при яких густина ймовірності буде найбільшою.

Оцінка густини ймовірності в мережі заснована на ядерних оцінках. Якщо приклад розташований в даній точці простору, тоді в цій точці є певна густина ймовірності. Кластери з близько розташованих точок, свідчать, що в цьому місці густина імовірності велика. Поблизу спостереження є більша довіра до рівня густини, а по мірі віддалення від нього довіра зменшується і плине до нуля. В методі ядерних оцінок в точку, що відповідає кожному прикладу, поміщається деяка проста функція, потім вони всі додаються і в результаті утворюється оцінка для загальної густини імовірності. Найчастіше в якості ядерних функцій беруть дзвоноподібні функції (гаусові). Якщо є достатня кількість навчальних прикладів, такий метод дає добрі наближення до істинної густини імовірності.

Імовірнісна мережа має три прошарки: вхідний, радіальний та вихідний. Радіальні елементи беруться по одному на кожний приклад. Кожний з них містить гаусову функцію з центром в цьому прикладі. Кожному класу відповідає один вихідний елемент. Вихідний елемент з'єднаний лише з радіальними елементами, що відносяться до його класу і підсумовує виходи всіх елементів, що належать до його класу. Значення вихідних сигналів утворюються пропорційно ядерних оцінок ймовірності приналежності відповідним класам.

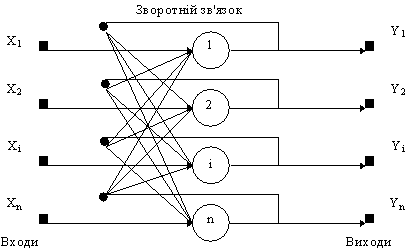
Рис. 8. Приклад імовірнісної нейронної мережі

Базова модель імовірнісної мережі має модифікації. Припустимо, що пропорції класів у навчальній множині відповідають їх пропорціям у всій досліджуваній вибірці (апріорна імовірність). Наприклад, якщо серед всіх людей хворими є 2%, то в навчальній множині для мережі, яка діагностує захворювання, хворих також повинно бути 2%. Якщо ж апріорні імовірності відрізняються від пропорції в навчальній виборці, мережа буде видавати невірний результат. Це можна врахувати, вводячи корегуючі коефіцієнти для різноманітних класів.

Навчання імовірнісної нейронної мережі є набагато простішим, ніж ВackРropagation. Істотним недоліком мережі є її розмір, оскільки вона фактично вміщує в собі всі навчальні дані, потребує багато пам'яті і може повільно працювати.

Мережа Хопфілда

Джон Хопфілд вперше представив свою асоціативну мережу у 1982 р. у Національній Академії Наук. На честь Хопфілда та нового підходу до моделювання, ця мережна парадигма згадується як мережа Хопфілда. Мережа базується на аналогії фізики динамічних систем. Початкові застосування для цього виду мережі включали асоціативну, або адресовану за змістом пам'ять та вирішували задачі оптимізації.

Мережа Хопфілда використовує три прошарки: вхідний, прошарок Хопфілда та вихідний прошарок. Кожен прошарок має однакову кількість нейронів. Входи прошарку Хопфілда під'єднані до виходів відповідних нейронів вхідного прошарку через змінні ваги з'єднань. Виходи прошарку Хопфілда під'єднуються до входів всіх нейронів прошарку Хопфілда, за винятком самого себе, а також до відповідних елементів у вихідному прошарку. В режимі функціонування, мережа скеровує дані з вхідного прошарку через фіксовані ваги з'єднань до прошарку Хопфілда. Прошарок Хопфілда коливається, поки не буде завершена певна кількість циклів, і біжучий стан прошарку передається на вихідний прошарок. Цей стан відповідає образу, вже запрограмованому у мережу.

Навчання мережі Хопфілда вимагає, щоб навчальний образ був представлений на вхідному та вихідному прошарках одночасно. Рекурсивний характер прошарку Хопфілда забезпечує засоби корекції всіх ваг з'єднань. Недвійкова реалізація мережі повинна мати пороговий механізм у передатній функції. Для правильного навчання мережі відповідні пари "вхід-вихід" мають відрізнятися між собою.

Якщо мережа Хопфілда використовується як пам'ять, що адресується за змістом вона має два головних обмеження. По-перше, число образів, що можуть бути збережені та точно відтворені є строго обмеженим. Якщо зберігається занадто багато параметрів, мережа може збігатись до нового неіснуючого образу, відмінному від всіх запрограмованих образів, або не збігатись взагалі. Межа ємності пам'яті для мережі приблизно 15% від числа нейронів у прошарку Хопфілда. Другим обмеженням парадигми є те, що прошарок Хопфілда може стати нестабільним, якщо навчальні приклади є занадто подібними. Зразок образу вважається нестабільним, якщо він застосовується за нульовий час і мережа збігається до деякого іншого образу з навчальної множини. Ця проблема може бути вирішена вибором навчальних прикладів більш ортогональних між собою.

Структурна схема мережі Хопфилда приведена на рис. 9.

Рис. 9. Структурна схема мережі Хопфілда.

Задача, розв'язувана даною мережею в якості асоціативної пам'яті, як правило, формулюється таким чином. Відомий деякий набір двійкових сигналів (зображень, звукових оцифровок, інших даних, що описують якийсь об'єкти або характеристики процесів), вважають зразковим. Мережа повинна вміти з зашумленого сигналу, поданого на її вхід, виділити ("пригадати" по частковій інформації) відповідний зразок або "дати висновок" про те, що вхідні дані не відповідають жодному із зразків. У загальному випадку, будь-який сигнал може бути описаний вектором x ₁, х_і, х_n..., n - число нейронів у мережі і величина вхідних і вихідних векторів. Кожний елемент x_i дорівнює або +1, або -1. Позначимо вектор, що описує k -ий зразок, через X_k, а його компоненти, відповідно, - x_ik, k =0,..., m -1, m - число зразків. Якщо мережа розпізнає (або "пригадує") якийсь зразок на основі пред'явлених їй даних, її виходи будуть містити саме його, тобто Y = X_k, де Y - вектор вихідних значень мережі: y ₁, y_i, y_n. У противному випадку, вихідний вектор не співпаде з жодний зразковим.

Якщо, наприклад, сигнали являють собою якесь зображення, то, відобразивши у графічному виді дані з виходу мережі, можна буде побачити картинку, що цілком збігається з однієї зі зразкових (у випадку успіху) або ж "вільну імпровізацію" мережі (у випадку невдачі).