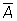Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи побудови функцій приналежності нечітких множинСодержание книги
Поиск на нашем сайте
У приведених вище прикладах використані прямі методи, коли експерт або просто задає для кожного xÎE значення mA(x), або визначає функцію приналежності. Як правило, прямі методи завдання функції приналежності використовуються для вимірних понять, таких як швидкість, година, відстань, тиск, температура і т.д., тобто коли виділяються полярні значення. У багатьох задачах при характеристиці об'єкта можна виділити набір ознак і для кожного з них визначити полярні значення, що відповідають значенням функції приналежності, 0 чи 1. Наприклад, у задачі розпізнавання обличчя можна виділити наступні пункти:
Для конкретного обличчя А експерт, виходячи з приведеної шкали, задає mA(x)Î [0,1], формуючи векторну функцію приналежності { mA(x1), mA(x2),... mA(x9)}. Непрямі методи визначення значень функції приналежності використовуються у випадках, коли немає елементарних вимірних властивостей, через які визначається потрібна нечітка множина. Як правило, це методи попарних порівнянь. Якби значення функцій приналежності були нам відомі, наприклад, mA(xi) = wi, i=1,2,...,n, тоді попарні порівняння можна представити матрицею відношень A = {aij}, де aij=wi/wj (операція ділення). Операції над нечіткими множинами Вміщення Нехай A і B - нечіткі множини на універсальній множині E. Говорять, що A міститься в B, якщо "x ÎE mA(x) <mB(x). Позначення: A Ì B. Іноді використовують термін "домінування", тобто у випадку коли A Ì B, говорять, що B домінує A. Рівність A і B рівні, якщо "xÎE mA(x) = mB (x). Позначення: A = B. Доповнення Нехай M = [0,1], A і B - нечіткі множини, задані на E. A і B доповнюють один одного, якщо "xÎE mA(x) = 1 - m B(x). Позначення: B = Очевидно, що Перетинання AÇB - найбільша нечітка підмножина, що міститься одночасно в A і B.
mAÇB(x) = min(mA(x), mB(x)). Об'єднання А È В - найменша нечітка підмножина, що включає як А, так і В, з функцією приналежності: mAÈ B(x) = max(mA(x), m B(x)). Різниця А - B = АÇ mA-B(x) = mA Ç Диз'юнктивна сума АÅB = (А - B)È(B - А) = (А Ç mA-B(x) = max{[min{m A(x), 1 - mB(x)}];[min{1 - mA(x), mB(x)}] } Приклади Нехай: A = 0,4/ x1 + 0,2/ x2+0/ x3+1/ x4; B = 0,7/ x1+0,9/ x2+0,1/ x3+1/ x4; C = 0,1/ x1+1/ x2+0,2/ x3+0,9/ x4. Тут: 1. AÌB, тобто A міститься в B чи B домінує A, С незрівнянно ні з A, ні з B, тобто парі {A, С} і {A, С} - парі недомінуємих нечітких множин. 2. A ¹ B ¹C. 3.
4. AÇB = 0,4/x1 + 0,2/x2 + 0/x3 + 1/x4. 5. АÈС = 0,7/x1 + 0,9/x2 + 0,1/x3 + 1/x4. 6. А - С = АÇ В - А = 7. А Å В = 0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.69.162 (0.007 с.) |

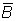 чи A =
чи A =