Загальна структура нечіткого мікроконтролера

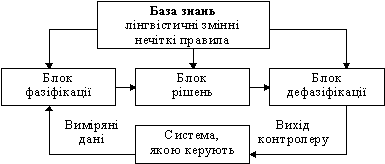
Загальна структура мікроконтролера, що використовує нечітку логіку, показана на рис.1. Вона містить у своєму складі наступні складові:

• блок фазіфікації;
• базу знань;
• блок рішень; блок дефазіфікації.

Блок фазіфікації перетворює чіткі величини, виміряні на виході об'єкта керування, у нечіткі величини, що описані лінгвістичними змінними в базі знань.

Блок рішень використовує нечіткі умовні (if - then) правила, закладені в базі знань, для перетворення нечітких вхідних даних у необхідні керуючі впливи, що носять також нечіткий характер.

Блок дефазіфікації перетворює нечіткі дані з виходу блоку рішень у чітку величину, що використовується для керування об'єктом.

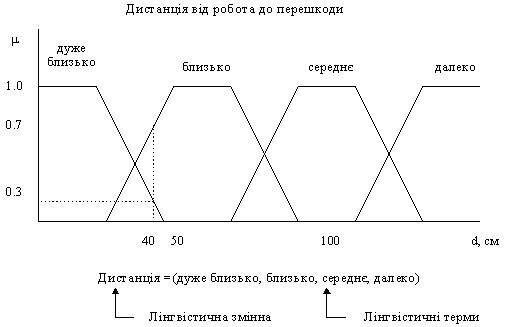
Рис. 1. Загальна структура нечіткого мікроконтролера

Як приклад відомих мікроконтролерів, що підтримують нечітку логіку можна назвати 68HC11, 68HC12 фірми Motorola, MCS-96 фірми Intel, а також деякі інші.

Всі системи з нечіткою логікою функціонують за одним принципом: показання вимірювальних приладів: фазіфікуються (перетворюються в нечіткий формат), обробляються, дефазіфікуються й у вигляді звичайних сигналів подаються на виконавчі пристрої.

Розглянемо випадок керування мобільним роботом, задачею якого є об'їзд перешкод. Введемо дві лінгвістичні змінні: ДИСТАНЦІЯ (відстань від робота до перешкоди) і НАПРЯМОК (кут між подовжньою віссю робота та напрямком на перешкоду).

Розглянемо лінгвістичну змінну ДИСТАНЦІЯ. Значеннями її можна визначити терми ДАЛЕКО, СЕРЕДНЕ, БЛИЗЬКО і ДУЖЕ БЛИЗЬКО. Для фізичної реалізації лінгвістичної змінної необхідно визначити точні фізичні значення термів цієї змінної. Нехай змінна ДИСТАНЦІЯ може приймати будь-які значення з діапазону від нуля до нескінченності. Відповідно до теорії нечітких множин, у такому випадку кожному значенню відстані з зазначеного діапазону може бути поставлене у відповідність деяке число від нуля до одиниці, що визначає ступінь приналежності даної фізичної відстані (припустимо 40 см) до того чи іншого терму лінгвістичної змінної ДИСТАНЦІЯ. Ступінь приналежності визначаємо функцією приналежності М(d), де d-відстань до перешкоди. У нашому випадку відстані 40 см. Можна задати ступінь приналежності до терму ДУЖЕ БЛИЗЬКО рівним 0,7, а до терму БЛИЗЬКО - 0,3 (рис. 2.). Конкретне визначення ступеня приналежності може проходити тільки при роботі з експертами.

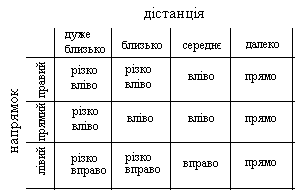
Рис. 2. Лінгвістична змінна і функція приналежності

Змінній НАПРЯМОК, яка може приймати значення в діапазоні від 0 до 360 градусів, задамо терми ЛІВИЙ, ПРЯМИЙ і ПРАВИЙ.

Тепер необхідно задати вихідні змінні. У даному прикладі достатньо однієї, яка назвемо РУЛЬОВИЙ КУТ. Вона може містити терми: РІЗКО ВЛІВО, ВЛІВО, ПРЯМО, ВПРАВО, РІЗКО ВПРАВО. Зв'язок між входом та виходом запам'ятовується в таблиці нечітких правил.

Таблиця нечітких правил

Кожний запис у даній таблиці відповідає своєму нечіткому правилу, наприклад: Якщо дистанція близько і напрямок правий, тоді рульовий кут різко вліво

Таким чином, мобільний робот з нечіткою логікою буде працювати за наступним принципом: дані з сенсорів про відстань до перешкоди та напрямок до неї будуть фазіфіковані, оброблені згідно табличних правил, дефазіфіковані і дані, що отримані, у вигляді керуючих сигналів надходять на приводи робота.

Нечітка логіка в Matlab

Fuzzy logic toolbox - вбудована в Matlab сукупність функцій, що містить набір засобів, які дозволяють:

• створювати і редагувати нечіткі системи всередині середовища Matlab;
• вбудовувати нечітку підсистему в SimuLink (поставляється з Matlab) при моделюванні загальної системи;
• побудувати нечітку систему в Matlab у вигляді процедури, що викликається з програми, яка написана на мові Сі.

Даний набір інструментів забезпечує три категорії інструментальних засобів програмування нечітких систем:

• функції командного рядка (command line functions);
• графічний інтерактивний інтерфейс;
• використання вбудованих блоків SimuLink.

Перша категорія - готові функції, які можна викликати відразу з командного рядка Matlab. Практично усі вони являють собою м-файли, що містять послідовність виразів, що виконують спеціалізований нечіткий алгоритм. Для перегляду вихідного коду функцій необхідно набрати в командному рядку:

type ім'я_функції

Крім того, Matlab дозволяє їх модифікувати шляхом копіювання і перейменування відповідного файлу та наступного його редагування. Таким чином, нечіткий набір інструментів є розширеним власними функціями.

Друга категорія дозволяє отримати доступ до тих самих функцій через графічний користувальницький інтерфейс, за допомогою якого набагато зручніше конструювати й аналізувати нечіткі системи.

Третя категорія - моделювання в середовищі SimuLink. Тут підсистеми представляються у виді блоків - можна з'єднати будь-яким чином і відразу отримати результати.

У Matlab є багато вбудованих функцій приналежності, зокрема:

• сигмоїдальна;
• двостороння сигмоїдальна;
• гаусова;
• дзвоноподібної форми
• S-функція приналежності;
• Z-функція приналежності;
• трапецієподібна;
• трикутна й ін.

Усі дії над нечіткими числами задаються мінімальним набором функцій і відбуваються всередині програми. Таким чином, користувачу необов'язково вивчати усі тонкощі теорії нечітких множин, достатньо лише визначити усі вхідні і вихідні змінні і задати таблицю правил, а решту роботи робить Matlab. Дефазіфікація виконується в один з п'ятьох методів, зазначених програмістом. Крім того, можна вивести на екран відповідно до введених правил результуючі поверхні керування в залежності від комбінації входів, схему отриманої нечіткої програми, і це лише мала частина всіх можливостей даного набору інструментів.

Переваги нечітких систем

Коротко перелічимо відмітні переваги fuzzy-систем у порівнянні з іншими: