
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика повышения логической культуры учащихся начальной и средней школы (из опытаСодержание книги
Поиск на нашем сайте
Работы) С целью поднятия логической культуры студентов - будущих педагогов автор разработал примерные задания по логике на период педагогической практики. В период непрерывной практики студентам IV курса отделения начальных классов МП ГУ им. В.И.Ленина рекомендовалось провести с учащимися 2, 3, 4 классов внеклассные занятия по теме «Понятие» по следующим разделам: 1.Отношения между понятиями. 2.Обобщение и ограничение понятий. 3.Определение понятий. 4.Деление понятий. 5.Объединение и пересечение понятий. 6.Логические ошибки учащихся в процессе оперирования понятиями. Содержание работы Отношения между понятиями рекомендуется разъяснять учащимся с помощью иллюстраций всех шести типов отношений понятий (тождественные; подчиненные и подчиняющие; перекрещивающиеся; соподчиненные; противоположные; противоречащие). Сначала можно взять примеры понятий по усмотрению самого практиканта и проиллюстрировать их отношения с помощью кругов Эйлера. Каждое понятие обозначается большой буквой (А, В, С...). Работа проводится со всеми учащимися одновременно. Затем рекомендуется всем студентам-практикантам предложить для самостоятельного решения задачи, одинаковые для всех классов, с целью в дальнейшем сравнить результаты работ учащихся 2, 3,4 классов и оценить быстроту и степень усвоения новых знаний. Контрольный вариант задач рекомендуется следующий (он уже был апробирован): 1.Первый летчик-космонавт, космонавт Юрий Алексеевич Гагарин. 2.а) Школьник, турист; б) Каменный дом, двухэтажный дом, трехэтажный дом. 3. а) Фигура, треугольник; б) Главный член предложения, подлежащее. 4.Скрипка, рояль, барабан, музыкальный инструмент. 5.Северный полюс, Южный полюс. 6.а) Великан, карлик; б) Глубокая река, мелкая река. После выполнения и проверки самостоятельных работ рекомендуется на следующем занятии провести анализ хороших работ и показать типы допущенных логических ошибок. Работы учащихся должны быть собраны и сданы преподавателю логики вместе с письменным отчетом о педпрактике (по логике). Обобщение и ограничение понятий также сначала следует разъяснить на своих примерах, затем предложить произвести обобщение понятий «березка», «ложка» и ограничение понятий «растение», «лодка». Необходимо выявить типичные ошибки, допущенные учащимися начальных классов в процессе осуществления операций обобщения и ограничения понятий. Деление понятий. После разъяснения этой операции на своих примерах рекомендуется провести операцию деления для понятий «треугольник» и «член предложения» (или понятия «звук»). Эти понятия уже известны учащимся начальных классов. Также необходимо дать классификацию ошибочных ответов учащихся, Определение понятий следует разъяснить на примерах, взятых из учебников 2, 3 и 4 класса, именно того класса, в котором проводятся занятия, Рекомендуется сказать учащимся и о правилах определения понятий и о типичных ошибках, возникающих при их нарушении. Следует предложить учащимся определить такие понятия: «компас», «квадрат», с которыми они познакомились на уроках. Операции объединения понятий и пересечения понятий1 (как показали эксперименты с учащимися 2, 3, 4 классов) не вызывают затруднений: школьники на уроках математики знакомились с этими операциями. После объяснения на своих примерах рекомендуется предложить учащимся произвести объединение понятий: а) «дерево» и «ель»; б) «инженер» и «изобретатель». Пересечение понятий можно сделать для следующих примеров; а) «студент» и «спортсмен»; б) «населенный пункт» и «город». Логические ошибки учащихся в процессе оперирования понятиями студент-практикант должен систематизировать сам на основе проведенных занятий с учащимися и в обобщенном виде включить в письменный отчет о проведении педпрактики по логике. Для ориентировки сообщаем, что таких типов ошибок в оперировании понятиями выявлено около 20. Особенно ценными будут не только простая констатация этих ошибок, а ваши конкретные предложения для учителя о приемах и методах преодоления логических ошибок, встречающихся у учащихся того или иного из начальных классов а ходе работы с понятиями. 2. Требования к оформлению работы 1. В письменном отчете о проведенной педпрактике по логике необходимо описать проведенные занятия с учащимися и сделать приложение по следующей схеме (см. табл. с. 323). В этой схеме правильное решение обозначено «+ «; «проп.» и «неполн.» обозначают (соответственно) то, что пропущены промежуточные понятия при ограничении или обобщении понятии или сделано неполное ограничение или обобщение; «скач.» означает скачок в делении, а «шир.» — широкое определение. Такая схема покажет ошибки в решении задач — их количество и типы, а также позволит выявить, какие задачи решены правильно. 3.Студент должен показать, на каких его собственных примерах производилось объяснение материала и дать правильное решение задач. 4.Работа должна содержать информацию о приемах работы студента- 5.Необходимо описать все типы логических ошибок, обнаруженных в ходе
5.Предъявить письменные работы учащихся, выполненные на стандарт 6.Найти в журнале «Начальная школа» статьи, посвященные развитию Письменный отчет покажет умение студента применять теоретические знания по логике в практике школьной работы. В период непрерывной педагогической практики студенты IV курса факультета начальных классов провели по 2-3 занятия но теме «Понятие» с учащимися начальных классов В г. Москве, и том числе с шестилетками. Студенты проводили или отдельные уроки, или внеклассные занятия, или занятия в группе продленного дня. Такую же работу с учащимися 4-10 классов в период педпрактики провели студенты П курса педагогического факультета. Эту работу под моим руководством проводили 200 студентов, охватив в обучении более 2500 учащихся. Такие занятия по логике у детей вызвали эмоционально-оживленный интерес; дети наперебой стремились отвечать у доски, они с большим желанием решали предложенные им задачи, обсуждали допущенные ошибки, эмоционально переживали неудачи. В своих подробных отчетах почти все студенты написали о необходимости проведения такой работы по логике с учащимися по развитию их логического мышления. Студенты вечернего отделения факультета начальных классов в 1987/88 учебном году провели такую же работу по теме «Понятие» со своими учащимися. Ранее, разумеется, они не проводили этой работы. По отзывам студентов-вечерников (уже работающих много лет учителями в начальных классах), ученики 1, 2, 3 классов были очень активны на занятиях по логике, и самим преподавателям эти занятия принесли большое моральное удовлетворение. Мы рекомендуем во время педпрактики студентов в качестве одной из форм внеклассной работы (или работы на уроках) проведение занятий по логике с учащимися всех классов школы. Преподаватель логики пединститута должен подобрать задачи по теме «Понятие» с учетом факультета, на котором изучается курс логики, школьного класса, программы и содержания школьного предмета, который будет преподавать студент-практикант. В 1987/88 учебном году студенты II курса педфака впервые провели педпрактику по темам «Суждение» и «Умозаключение», Они получили следующие задания. Задания по логике для студентов второго курса на период педагогической практики в 1987/88 учебном году Рекомендуется провести 2-3 внеклассных занятия (или занятия в группе продленного дня) с учащимися 2-10 классов по темам «Суждение» и «Умозаключение». Желательно сначала провести занятия, на которых объясняется материал, а затем — контрольного характера. По теме «Суждение» рекомендуется объяснить следующий материал: 1.Определение суждения. Структура простого суждения. 2.Виды простых суждений. 3.Объединенная классификация простых категорических суждений по 4.Сложное суждение и его виды: (а Отрицание суждения (a). В зависимости от класса методика объяснения и приведения примеров разрабатывается самим студентом-практикантом. Для начальных классов она будет одной, для средних — другой, а для старших (например, 10 и 11 классов) приближается к вузовской методике со внесенными практикантом упрощениями примеров. Приведем примерное объяснение материала для учащихся средних классов: 1.Определение суждения дано в учебнике (с. И, 60). Примеры можно 2.Структура суждения: субъект, предикат, связка, кванторное слово - 3.Объяснение видов простых суждений и суждений А, I, E, О, как нам Раздел «Сложное суждение и его виды» потребует введения логических знаков: 1. «Прозрачный лес один чернеет, и ель сквозь иней зеленеет, и речка по а 2.Этот юноша — футболист, или он шахматист. 3.Я поеду на Юг поездом или полечу самолетом. a v b(«v» — союз «или» строгий: в каждый данный момент времени можно делать только одно}. 4.Если будет хорошая погода, то мы пойдем на экскурсию. 5. a Ни один кит не является рыбой. = Ни одна рыба не является китом. 6. Я завтра пойду на тренировку (а). Я завтра не пойду на тренировку (а). Учащиеся должны придумать свои примеры на каждый вид логических связок (1-6). После этого студент предлагает своим учащимся ряд задач, требующих записи сложного суждения в виде формулы. Например: 1. «Если мальчик любит мыло и зубной порошок, этот мальчик очень милый, поступает хорошо» (В.Маяковский). Формула (а В качестве упражнений можно взять задачи данного учебника, приведенные нас. 90, задание III (1-3), ответы для которых будут следующими: 1.Формула первого сложного суждения: а 2.а 3. а Для учащихся старших классов можно в качестве примеров взять и задачи на с. 91-92, задание VII (1-7). По теме «Умозаключение» рекомендуется объяснить следующий материал: 1.Определение и структура умозаключений. 2.Дедуктивные умозаключения: а) категорический силлогизм; б) энтимема; в) условно-категорические умозаключения; г) разделительно-категорические умозаключения; д) конструктивные дилеммы. Рекомендуем привести 2-3 примера правильно построенных категорических силлогизмов, дающих истинное заключение, и примеры неправильно построенных, дающих вероятное заключение, и обратить внимание учащихся на возможные ошибки. Все металлы теплопроводны. Медь — металл.__ Медь теплопроводна. Все тигры полосатые. Это животное полосатое. Это животное — тигр. Учащиеся смогут привести аналогичные примеры. Энтимема объясняется школьникам на только что приведенных самим студентом или учащимся примерах. Пропускается либо большая посылка, либо меньшая, либо заключение. Разъясняется, что мы мыслим каждый день с помощью энтимем и реже — с помощью категорических силлогизмов. Условно-категорические и разделительно-категорические умозаключения разъясняются на примерах и строятся соответствующие формулы. Показываются примеры на достоверные и на вероятные модусы условно - категорических умозаключений на материале школьных учебников. Разъясняя разделительно-категорические умозаключения, практикант должен обратить внимание, чтобы в разделительной посылке были перечислены все возможные альтернативы, т.е. деление было бы полным (для отрицающее -утверждающего модуса). Отчет студента о проведенной работе должен состоять из следующих разделов: 1.Описать проведенные с учащимися занятия. 2.Сделать анализ ошибок (по произвольной схеме). 3. Предъявить письменные работы учащихся с указанием фамилии Опыт проведения педпрактики по логике в школах г. Москвы показал, что многие учителя школ сами логику не изучали, не знают ее применения в учебном процессе, а некоторые просто не понимают, зачем она нужна учащимся. Школьники встретили изучение логики с большим интересом, многие просили студентов еще провести с ними такого рода занятия. Педагогам, как никому другому, надо развивать логическое, творческое мышление своих учащихся, а они сами не изучали логики. Парадокс! Его можно и нужно разрешить. Преподаватель логики пединститута мог бы написать о результатах проведенной им новой, оригинальной работы с учащимися средних и старших классов В журналы «Математика в школе», «История в школе», «Физика в школе» и др. Так как в этих журналах публикуется мало статей о развитии логического мышления учащихся, то такая работа преподавателя логики была бы очень актуальна, ценна и полезна как для учителей школ, так и для студентов пединститутов и педучилищ. Студенты МПГУ им. В.И. Ленина провели огромную оригинальную работу, которая только что была показана выше. Насколько нам известно, в других педвузах подобная работа не ведется. 200 студентов смогли дать уроки по логике более 2500 учащимся. Несколько лет назад мы сформулировали педагогическую гипотезу — логику надо вводить как обязательный предмет в начальных классах средней школы. Хорошо логику воспринимают уже учащиеся 2 класса. Эта гипотеза получила свое научное и методическое подтверждения. Чтобы ее подтвердить, автор данного учебника начал преподавать логику сначала в 5, 8, 10 и 11 классах средней школы № 583 г Москвы по своим программам. Следует отметить, что учащиеся как 8, так и 10 и 11 классов с одинаковой быстротой овладевают теоретическим материалом и решают логические задачи. Контрольные, проведенные по тем же вариантам и тем же задачам, которые давались для студентов I курса педвуза, свидетельствуют о том, что логику необходимо вводить в курс средней школы, и не в 11 классе, а раньше. В той же школе в течение трех четвертей учебного года логику преподавал доктор философских наук, профессор А.Л.Никифоров в двух 10 классах экономического профиля. Его учащиеся успешно овладели основами логики, с интересом решали задачи и приводили свои примеры на материале экономики. Оригинальными были занятия по логике А.Д. Гетмановой в этой же школе с учащимися 5 класса. Это был годовой курс. Такой огромной заинтересованности, быстроты мышления и оригинальности я и не предполагала. Ученикам-пятиклассникам и мне эти уроки приносили настоящую интеллектуальную радость, подъем, часто они не хотели уходить, хотя эти были 6-й и 7-й уроки. Начало было в 5 классе не совсем удачным: весь класс не «потянул» обязательный курс логики, поэтому мы перешли на факультативные занятия, которые посещали 10-12 человек. Но это были действительно заинтересованные ученики-энтузиасты, они настаивали на проведении уроков логики и боялись, что занятия могут прерваться. Материал по логике пятиклассникам я специально давала по программе, приближенной к 10 классу, и они все понимали, решали, приводили массу оригинальных примеров, рассуждений. Это часто был праздник мысли, интеллекта и для них, и для меня. Особенно эффективны были последние два урока, когда мы решали задачи из книги известного психолога Г. Айзенка «Проверьте свои интеллектуальные способности» (Рига, 1992). Некоторые задачи воспроизведены здесь в фотокопии. Пятиклассники решали их быстрее, интереснее, чем взрослые. В книге Айзенка написано, что эти задачи предназначены людям от 18 до 50-60 лет, но мои 11-летние ученики смело опровергли знаменитого автора: они отлично справлялись с задачами, лишь изредка заглядывая в данный в книге ответ, если не могли решить задачу. Все учащиеся 5 класса получили годовой зачет с оценкой «отлично». Я же получала огромный эмоциональный положительный заряд от каждого общения с этими ребятами (в основном это были мальчики и 3 девочки). Ум у пятиклассников острый, подвижный, незакостеневший. Ученики 10 класса школы № 248 (школа с профилирующим преподаванием английского языка), где логика преподавалась мною факультативно, также поразили меня своей общей эрудицией, большим чувством юмора. Уроки по логике часто проходили очень весело, приводилось много остроумных примеров, анекдотов из литературных источников, веселых историй из школьной жизни. Впечатление от этих уроков осталось самым светлым, иногда они живее схватывали материал и реагировали даже острее, чем отдельные студенты. Однако формирование логической культуры желательно начинать не со старших, а с первого класса начальной школы. Мой опыт преподавания логики в трех школах г. Москвы и Московской области в 1, 2,3,4,5 классах убедительно доказал, что ученики начальных классов успешно овладевают логическими знаниями. Уроки базируются на большом, ярко иллюстрированном художественном материале из детских народных сказок, детской художественной литературы, природоведения, математики и других предметов. Неоднократные наблюдения в течение последних лет моего преподавания логики в начальных классах показали, что ученикам 1 -3 классов доставляет интеллектуальное удовольствие решение задач на нахождение отношений между понятиями (например, «игрушка», «заводная игрушка», «заводной автомобиль», «кукла», «кукла Барби»), Используя разноцветные кружки (круги Эйлера), приготовленные ими на уроках труда, дети решают аналогичные задачи. Уже на первом и втором уроках первоклассники в стихотворении находят понятия и суждения, почти безошибочно отличая одну форму мышления от другой. В дальнейшем они придумывают свои примеры на различные виды умозаключений. Сложные суждения учащиеся выражают формулами типа (A На уроках решались шарады, отгадывались загадки и кроссворды, применялись многочисленные ярко раскрашенные рисунки, изготовленные студентами педагогических университетов г. Москвы, пелись песни, использовались подвижные игры и другие разнообразные методы обучения. Курс логики в средней школе изучается в основном в 10 и II классах. Опыт такого преподавания намного шире, чем у младших школьников. Имеется программа для общеобразовательных учреждений «Логика» (58 часов), которая рекомендована Главным управлением развития общего среднего образования Министерства образования Российской Федерации (М., Просвещение, 1994). В соответствии с этой программой написано учебное пособие «Логика, 10-11-е классы», в которой наряду с теоретическими разделами даются задачи по курсу логики и занимательные задачи. Авторами являются доктора философских наук, профессора А.Д. Гетманова, А.Л.Никифоров, М.И.Панов, А.И. Уемов, Б.Л.Яшин, Ученики 10-11 классов школы № 356 и Люблинской гимназии (г. Москва) изготовили много интересных, оригинально иллюстрированных работ и наглядных пособий, а после изучения спецкурса по теории аргументации учащиеся гимназии провели ряд диспутов на молодежные темы. В.А. Ширнин преподает логику в общеэстетической школе-гимназии № 676 г. Москвы и средней школе № 26 г. Воскресенска главным образом в 10-11 классах и в 5-8 классах. В.А. Ширнин применяет необычные формы ведения уроков и подбирает запоминающиеся примеры для иллюстрации теоретического материала. Два года в школе-гимназии № 676 ребята в качестве экзамена по выбору сдают логику в форме защиты рефератов на темы: «Логические основы формирования понятий (на основе понятия «мода»)», «Популярное объяснение младшим школьникам, что такое умозаключение и дедукция (с иллюстрациями автора)» и др. В марте 1994 г. Ширнин провел трехдневный семинар для 30 учителей Воскресенского района, желающих преподавать логику в школе. Ведущий семинара Ширнин получил положительные отзывы, и слушатели изъявили желание продолжить эти занятия. Участники семинара высоко оценили указанное выше учебное пособие по логике для 10-11 классов и выразили готовность заниматься по данному пособию с учащимися своих школ. Преподаватель Л.П. Заросилова в Московском музыкально-театральном лицее в течение 1991/92 уч. г. проводила эксперимент по преподаванию логики учащимся 1-11 классов. Были отмечены успехи учащихся и их определенный, логически оформленный стиль высказывания по общим и специальным предметам: театроведению, сольфеджио, ритмике, эстетике и др. Итак, материал, изложенный в этой главе, позволяет сделать вывод, что логику как обязательный предмет надо вводить в средней школе и во всех типах педагогических учебных заведений, ибо логика лежит в основе гуманитаризации системы народного образования. И это — главное направление логического образования. В соответствии с ним изложен материал в данном учебнике. Другое направление заключается в том, чтобы дать лишь основы логических знаний и сделать это в процессе преподавания школьных дисциплин: математики, информатики, русского языка, физики, биологии, истории, литературы и др. Однако накопленного опыта такого обучения на сегодняшний день недостаточно. И хорошо, что работа в этом направлении ведется. Преподает логику во взаимосвязи с информатикой Путилло Л.В. (лицей, г. Лобня Моск. обл.). В школах г. Москвы преподают логику во взаимосвязи с информатикой учителя: Бримечкова В.А. (шк. № 134), Горшкова Г.В. (шк. № 947), Танцорова М.В. (шк. № 639), Трофимова М.В. (шк. № 876). Ничикова Е.В. связывает преподавание логики с психологией, а Курчаткина И.Е. (шк. № 134) логические знания дает на уроках физики. Тихомирова О. В. преподает логику студентам-юристам в тесной связи с юриспруденцией, правом и другими юридическими знаниями. Учитель школы № 931 г. Москвы Миронова Е.В. преподает логику в 11 педклассе, связывая логические знания с материалом русского языка и литературы. Щеколдина Н.С. (шк. № 789) в 5-7 и 11 классах на уроках русского языка использовала правила определения понятий, дихотомическое деление, классификацию понятий, обобщение и ограничение понятий, показывала нарушения логического закона тождества. На уроках литературы она подробно анализировала приемы, сходные с определением понятий, обращалась к объяснению аналогии, учила находить и формулировать дилеммы, стоящие перед литературными героями. Таким образом, повышение логической культуры школьников может осуществляться либо посредством систематического преподавания логики в 1-11 классах, либо путем введения ее основ при изучении отдельных предметов. Необходимо совершенствовать эту важнейшую научно-методическую работу по обоим направлениям. Глава X
|
||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.012 с.) |


 b ), {a v b ), (a v b), (a
b ), {a v b ), (a v b), (a  b), (a
b), (a 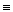 b).
b).


