
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратное уравнение. Полное, неполное квадратное уравнение. Исследование корней квадратного уравнения в зависимости от знака дискриминанта.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Квадратное уравнение. Полное, неполное квадратное уравнение. Исследование корней квадратного уравнения в зависимости от знака дискриминанта. Квадратным уравнением называется уравнение вида
где x - переменная, a,b,c - постоянные (числовые) коэффициенты. В общем случае решение квадратных уравнений сводится к нахождению дискриминанта:
О корнях квадратного уравнения можно судить по знаку дискриминанта (D):
В общем случае корни уравнения равны:
Очевидно, в случае с нулевым дискриминантом, оба корня равны
Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:
В таком случае корни уравнения вычисляются по формуле:
Теорема Виета. Приведенным квадратным уравнением называется уравнение вида
то есть квадратное уравнение с единичным коэффициентом при старшем члене. В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:
ax2 + bx = 0, a≠0, b≠0 Пусть неполное квадратное уравнение имеет вид 1. Вынесем общий множитель Мы получим
2. Решаем получившуюся систему уравнений. Решив эту систему, мы получим
Существование корней квадратного уравнения Для того чтобы квадратное уравнение ах 2 + bх + с = 0 имело корни необходимо и достаточно чтобы дискриминант уравнения был больше или равен нулю. Как правило, в случае необходимости доказать, что заданное квадратное уравнение имеет решение, начинают с вычисления его дискриминанта, с тем чтобы затем доказать его неотрицательность. Но существуют способы, которые основываются на очевидных графических соображениях. Так, если а > 0, то для доказательства того, что уравнение ах 2 + bx + с = 0 имеет два решения, достаточно указать одну точку х 0, в которой f(x 0 ) = ах 02 + bx 0 + c < 0. Чаще всего в качестве х 0 берут 0 (даёт достаточное условие с < 0), 1 (условие а + b + с < 0) или – 1 (условие а – b + c < 0).
Основные свойства функций. 1) Область определения функции и область значений функции. Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. В элементарной математике изучаются функции только на множестве действительных чисел. 2) Нули функции. Значения х, при которых y=0, называется нулями функции. Это абсциссы точек пересечения графика функции с осью Ох.
3) Промежутки знакопостоянства функции. Промежутки знакопостоянства функции – такие промежутки значений x, на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.
4) Монотонность функции. Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции. Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
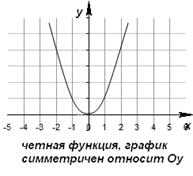
5) Четность (нечетность) функции. Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат. Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат. Четная функция обладает следующими свойствами:
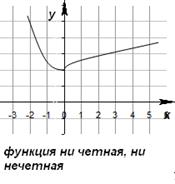
Нечетная функция обладает следующими свойствами: Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
6) Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная.
7) Периодическость функции. Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы). Функция f называется периодической, если существует такое число, что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T). T - это период функции. Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период. Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.
Свойства степеней Основные свойства степеней с целым показателем: am *an = a(m+n); am: an = a(m-n) (при a не равном нулю); (am)n = a(m*n); (a*b)n = an *bn; (a/b)n = (an)/(bn) (при b не равном нулю); a1 = a; a0 = 1 (при a не равном нулю); Эти свойства будут справедливы для любых чисел a, b и любых целых чисел m и n. Стоит отметить также следующее свойство: Если m>n, то am > an, при a>1 и am Можно обобщить понятие степени числа на случаи, когда в качестве показателя степени выступают рациональные числа. При этом хотелось бы, чтобы выполнялись все выше перечисленные свойства или хотя бы часть из них. Например, при выполнении свойства (am)n = a(m*n) выполнялось бы следующее равенство: (a(m/n))n = am. Это равенство означает, что число a(m/n) должно являться корнем n-ой степени из числа am. Степенью некоторого числа a (большего нуля) с рациональным показателем r = (m/n), где m – некоторое целое число, n – некоторое натурально число большее единицы, называется число n√(am). Исходя из определения: a(m/n) = n√(am). Для всех положительных r будет определена степень числа нуль. По определению 0r = 0. Отметим также, что при любом целом, любых натуральных m и n, и положительном а верно следующее равенство: a(m/n) = a((mk)/(nk)). Например: 134(3/4) = 134(6/8) = 134(9/12). Из определения степени с рациональным показателем напрямую следует тот факт, что для любого положительного а и любого рационального r число ar будет положительным. Свойства степеней. Для любых целых чисел m и p:
Свойства 1 - 5 справедливы Рис. II.1. При n=2 получаем функцию y = х2, ее свойства: Функция у —х2. Перечислим свойства функции у = х2. Область определения функции — вся числовая прямая. у = х2— четная функция (f(— х) = (— x)2 = x2 = f (х)). На промежутке [0; + οο) функция возрастает. В самом деле, если 4) На промежутке (- В самом доле, если
(-х1)2> (- х2)2, т. е.
Рис. II.2. При n = 3 получаем функцию у = х3, ее свойства: Область определения функции — вся числовая прямая. y = х3 — нечетная функция (f (- х) = (- x)2 = - х3 = - f (x)).
График (кубическая парабола) изображен на рисунке II.3. Рис. II.3. Пусть n— произвольное четное натуральное число, большее двух: n = 4, 6, 8,.... В этом случае функция у = хn обладает теми же свойствами, что и функция у = х2. График такой функции напоминает параболу у = х2, только ветви графика при |n| >1 тем круче идут вверх, чем больше n, а при Пусть n — произвольное нечетное число, большее трех: n = = 5, 7, 9,.... В этом случае функция у = хn обладает теми же свойствами, что и функция у = х3. График такой функции напоминает кубическую параболу (только ветви графика тем круче идут вверх, вниз, чем больше n. Отметим также, что на промежутке (0; 1) график степенной функции у = хn тем медленнее отдаляется от оси х с ростом х, чем больше n. Степенная функция с целым отрицательным показателем. Рассмотрим функцию у = х-n, где n — натуральное число. При n = 1 получаем у = х-n или у =
Рис. II.4. график функции у = Функция определена при всех х y = y = убывает на (0; +оо) и возрастает на (—оо;0). Теми же свойствами обладают любые функции вида y = х-n при четном n, большем двух. График функции у = Функции вида Степенная функция с положительным дробным показателем. Рассмотрим функцию у = хr, где r — положительная несократимая дробь. Перечислим некоторые свойства этой функции. Область определения — луч [0; + оо). Рис. II.5. На рисунке II.5. изображен график функции Подобный вид имеет график любой функции вида у = хr, где На том же рисунке изображен график функции Степенная функция с отрицательным дробным показателем. Рассмотрим функцию у = х-r, где r — положительная несократимая дробь. Перечислим свойства этой функции.
Область определения — промежуток (0; + оо). Рис. II.6. Свойства логарифмов Пусть 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) Определение Выражение Натуральный логарифм — это логарифм по основанию e. Обозначается lnx. Переход к новому основанию
ЛОГАРИФМИРОВАНИЕ. ГРАФИЧЕСКИЙ СПОСОБ. Многие уравнения, содержащие переменную не только под знаком логарифма или в показателе степени, удобно решать графически. Графически решением уравнения являются абсциссы точек пересечения графиков функций, заданных в уравнении. МЕТОД ПОДБОРА. Радианная мера угла. Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан. Градусная мера угла в 1 радиан равна: Так как дуга длиной π R (полуокружность), стягивает центральный угол в 180 °, то дуга длиной R, стягивает угол в π раз меньший, т.е.
И наоборот
Так как π = 3,14, то 1 рад = 57,3° Если угол содержит a радиан, то его градусная мера равна
И наоборот
Обычно при обозначении меры угла в радианах наименование «рад» опускают. Например, 360° = 2π рад, пишут 360° = 2π В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.
Косинус Косинусом числа а называется абсцисса точки, изображающей это число на числовой окружности. Косинусом угла в а радиан называется косинус числа а. Косинус - функция числа. Ее область определения - множество всех чисел, так как у любого числа можно найти ординату изображающей его точки. Область значений косинуса - отрезок от -1 до 1, так как любое число этого отрезка на оси абсцисс является проекцией какой-либо точки окружности, но никакая точка вне этого отрезка не является проекцией какой-либо из этих точек. Период косинуса равен Знак косинуса: 1. косинус равен нулю при 2. косинус положителен при 3. косинус отрицателен при Косинус - функция четная. Во-первых, область определения этой функции есть множество всех чисел, а значит,
1. Косинус возрастает на отрезках 2. Косинус убывает на отрезках
Тангенс Тангенсом числа называется отношение синуса этого числа к косинусу этого числа: Тангенсом угла в а радиан называется тангенс числа а.
Тангенс - функция числа. Ее область определения - множество всех чисел, у которых косинус не равен нулю, так как никаких других ограничений в определении тангенса нет. И так как косинус равен нулю при Область значений тангенса - множество всех действительных чисел. Период тангенса равен Знак тангенса: тангенс - отношение синуса к косинусу. Значит, он 1. равен нулю, когда синус равен нулю, то есть при 2. положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при 3. отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при Тангенс - функция нечетная. Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых, Вот и получилось, что Значит, тангенс возрастает на каждом участке своей области определения, то есть на всех интервалах вида Котангенс Котангенсом числа называется отношение косинуса этого числа к синусу этого числа: Область значений котангенса - множество всех действительных чисел. Период котангенса равен Знак котангенса: котангенс - отношение косинуса к синусу. Значит, он 1. равен нулю, когда косинус равен нулю, то есть при 2. положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при 3. отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при Котангенс - функция нечетная. Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых, В силу нечетности синуса и четности косинуса, числитель полученной дроби равен Вот и получилось, что
Квадратное уравнение. Полное, неполное квадратное уравнение. Исследование корней квадратного уравнения в зависимости от знака дискриминанта. Квадратным уравнением называется уравнение вида
где x - переменная, a,b,c - постоянные (числовые) коэффициенты. В общем случае решение квадратных уравнений сводится к нахождению дискриминанта:
О корнях квадратного уравнения можно судить по знаку дискриминанта (D):
В общем случае корни уравнения равны:
Очевидно, в случае с нулевым дискриминантом, оба корня равны
Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:
В таком случае корни уравнения вычисляются по формуле:
Теорема Виета. Приведенным квадратным уравнением называется уравнение вида
то есть квадратное уравнение с единичным коэффициентом при старшем члене. В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:
ax2 + bx = 0, a≠0, b≠0 Пусть неполное квадратное уравнение имеет вид 1. Вынесем общий множитель Мы получим
2. Решаем получившуюся систему уравнений. Решив эту систему, мы получим
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 8242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.221.45 (0.016 с.) |

 ,
, .
.
 .
. .
.
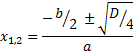
 ,
, .
.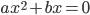 , где a ≠ 0; b≠ 0. В левой части этого уравнения естьобщий множитель
, где a ≠ 0; b≠ 0. В левой части этого уравнения естьобщий множитель 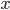 .
. . Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем
. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем  или
или  . Таким образом, данное уравнение эквивалентно двум уравнениям:
. Таким образом, данное уравнение эквивалентно двум уравнениям:
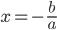 . Следовательно, данное квадратное уравнение имеет два корня
. Следовательно, данное квадратное уравнение имеет два корня 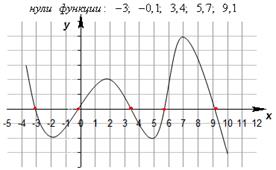







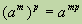

 .
. , не равных 0; свойство 6 -
, не равных 0; свойство 6 -  указанных
указанных 
 , то
, то 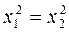 , а это и означает возрастание функции.
, а это и означает возрастание функции. ; 0] функция убывает.
; 0] функция убывает. , а это и означает убывание функции.
, а это и означает убывание функции. Графиком функции y=х2 является парабола. Этот график изображен на рисунке II.2.
Графиком функции y=х2 является парабола. Этот график изображен на рисунке II.2. 3) Функция y = x3 возрастает на всей числовой прямой. График функции y = x3 изображен на рисунке. Он называется кубической параболой.
3) Функция y = x3 возрастает на всей числовой прямой. График функции y = x3 изображен на рисунке. Он называется кубической параболой. тем «теснее прижимаются» к оси х, чем больше n.
тем «теснее прижимаются» к оси х, чем больше n. Свойства этой функции:
Свойства этой функции: График (гипербола) изображен на рисунке II.4.
График (гипербола) изображен на рисунке II.4. .
. 0.
0. , если n = 4, 6,....
, если n = 4, 6,.... ,
,  ,
,  обладают теми же свойствами, как и функция
обладают теми же свойствами, как и функция  .
. Он заключен между графиками функций у = х2 и у = х3, заданных на промежутке [0; + оо).
Он заключен между графиками функций у = х2 и у = х3, заданных на промежутке [0; + оо). .
. . Подобный вид имеет график любой степенной функции у = хr, где
. Подобный вид имеет график любой степенной функции у = хr, где  .
. Тогда:
Тогда:

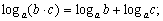


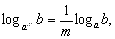






 Тогда и только тогда, когда
Тогда и только тогда, когда 
 тогда и только тогда, когда
тогда и только тогда, когда 
 тогда и только тогда, когда
тогда и только тогда, когда 
 с учетом того, что
с учетом того, что  называется - основным логарифмическим тождеством.
называется - основным логарифмическим тождеством. , частности, если c = b, то
, частности, если c = b, то 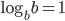 , и тогда:
, и тогда:





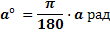
 . Ведь через каждые
. Ведь через каждые  , где n - любое целое число;
, где n - любое целое число;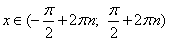 , где n - любое целое число;
, где n - любое целое число; , где n - любое целое число.
, где n - любое целое число. симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их абсциссы - косинусы - окажутся равными. То есть
симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их абсциссы - косинусы - окажутся равными. То есть для любого x.
для любого x. , где n - любое целое число.
, где n - любое целое число. , где n - любое целое число.
, где n - любое целое число.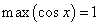 при
при  ;
;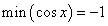 при
при  .
. .
. , где
, где 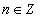 .
. . Ведь если взять любые два допустимые значения x (не равные
. Ведь если взять любые два допустимые значения x (не равные  ), отличающиеся друг от друга на
), отличающиеся друг от друга на 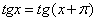 , то есть число
, то есть число  , где n - любое целое число.
, где n - любое целое число. , где а - любое целое число.
, где а - любое целое число. , где а - любое целое число.
, где а - любое целое число. . В силу нечетности синуса и четности косинуса, числитель полученной дроби равен
. В силу нечетности синуса и четности косинуса, числитель полученной дроби равен  , а ее знаменатель равен
, а ее знаменатель равен 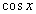 , а значит, сама эта дробь равна
, а значит, сама эта дробь равна  .
. .
. , где а - любое целое число.
, где а - любое целое число. . Котангенсом угла в а радиан называется котангенс числа а. Котангенс - функция числа. Ее область определения - множество всех чисел, у которых синус не равен нулю, так как никаких других ограничений в определении котангенса нет. И так как синус равен нулю при
. Котангенсом угла в а радиан называется котангенс числа а. Котангенс - функция числа. Ее область определения - множество всех чисел, у которых синус не равен нулю, так как никаких других ограничений в определении котангенса нет. И так как синус равен нулю при  , где
, где 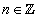
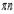 ), отличающиеся друг от друга на
), отличающиеся друг от друга на  , то есть, что число
, то есть, что число 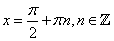 .
. .
.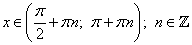 .
. .
. .
. . Котангенс убывает на каждом участке своей области определения, то есть на всех интервалах вида
. Котангенс убывает на каждом участке своей области определения, то есть на всех интервалах вида  .
.



