Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логарифмические неравенства, основные способы решения.Содержание книги
Поиск на нашем сайте Неравенства вида logax>b (logax≥b) или logax<b (logax≤b), где a>0, a≠1, называются простейшими логарифмическиминеравенствами. Решение логарифмических неравенств основано на строгой монотонности логарифмической функции. Известно, что o при основании, большем единицы, логарифмическая функция возрастает, o при положительном основании, меньшем единицы, логарифмическая функция убывает. Неравенство вида эквивалентно следующим системам неравенств o при a>1 f(x)>0, f(x)>ab; o при 0<a<1 f(x)>0, f(x)<ab. Неравенство вида эквивалентно следующим системам неравенств o при a>1 f(x)>0, f(x)<ab; o при 0<a<1 f(x)>0, f(x)>ab. Пример. Решить неравенство log8(x2-4x+3)<1. Решение. Так как основание логарифма больше единицы (а=8), то данное неравенство эквивалентно системе:
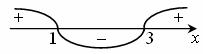
Каждое неравенство решим методом интервалов. х2-4x+3=0 при х1=1, х2=3. Определяя знаки, получим:
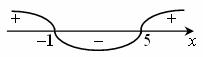
х2-4x-5=0 при х1=-1, х2=5. Определяя знаки, получим
Совмещая промежутки, имеем:
Таким образом, Ответ: Неравенство вида эквивалентно следующим системам неравенств: o при a>1 f(x)>0, g(x)>0, f(x)>g(x); o при 0<a<1 f(x)>0, g(x)>0, f(x)<g(x). Неравенство вида эквивалентно следующим системам неравенств o при a>1 f(x)>0, g(x)>0, f(x)<g(x); o при 0<a<1 f(x)>0, g(x)>0, f(x)>g(x). Пример. Решить неравенство:
Решение. Основание логарифмической функции меньше 1 (a=0,2). Поэтому, выписывая области определения выражений левой и правой частей неравенства и пользуясь свойством монотонности, получим равносильную систему: Решение неравенств второй степени методом интервалов:
Совмещая промежутки, получим:
Ответ: (-2;1). Более сложные логарифмические неравенства сводятся к простейшим методами, аналогичными используемым при решении логарифмических уравнений. Пример 1. Решить неравенство:
Решение. Переходя к основанию 2 в выражении, стоящем в правой части данного неравенства, получим:
Теперь перейдем к равносильной системе:
Решение встречающихся квадратичных неравенств провели методом интервалов:
Совмещая промежутки, получим
Ответ: (0; 2). Если в неравенстве встречается логарифмическая функция, содержащая неизвестное в основании, то, как правило, следует рассматривать два случая: o когда основание больше 1 o когда основание положительно, но меньше 1. Неравенство с переменным основанием можно также решать, используя формулы перехода к новому, не содержащему неизвестное, основанию.
Радианная мера угла. Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан. Градусная мера угла в 1 радиан равна: Так как дуга длиной π R (полуокружность), стягивает центральный угол в 180 °, то дуга длиной R, стягивает угол в π раз меньший, т.е.
И наоборот
Так как π = 3,14, то 1 рад = 57,3° Если угол содержит a радиан, то его градусная мера равна
И наоборот
Обычно при обозначении меры угла в радианах наименование «рад» опускают. Например, 360° = 2π рад, пишут 360° = 2π В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

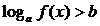

 или
или  .
.

 .
. .
.

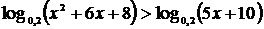 .
. .
.


 .
.
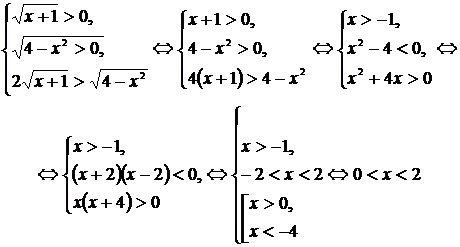


 .
.