
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства тригонометрических функций: Четность, нечетность, периодичность. Знаки значений тригонометрических функций по четвертям.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Синусом числа а называется ордината точки, изображающей это число на числовой окружности. Синусом угла в а радиан называется синус числа а. Синус - функция числа x. Ее область определения - множество всех чисел, так как у любого числа можно найти ординату изображающей его точки. Область значений синуса - отрезок от -1 до 1, так как любое число этого отрезка на оси ординат является проекцией какой-либо точки окружности, но никакая точка вне этого отрезка не является проекцией какой-либо из этих точек. Период синуса равен Знак синуса: 1. синус равен нулю при 2. синус положителен при 3. синус отрицателен при , где n - любое целое число. Синус - функция нечетная. Во-первых, область определения этой функции есть множество всех чисел, а значит, 1. Синус возрастает на отрезках 2. Cинус убывает на отрезке
Косинус Косинусом числа а называется абсцисса точки, изображающей это число на числовой окружности. Косинусом угла в а радиан называется косинус числа а. Косинус - функция числа. Ее область определения - множество всех чисел, так как у любого числа можно найти ординату изображающей его точки. Область значений косинуса - отрезок от -1 до 1, так как любое число этого отрезка на оси абсцисс является проекцией какой-либо точки окружности, но никакая точка вне этого отрезка не является проекцией какой-либо из этих точек. Период косинуса равен Знак косинуса: 1. косинус равен нулю при 2. косинус положителен при 3. косинус отрицателен при Косинус - функция четная. Во-первых, область определения этой функции есть множество всех чисел, а значит,
1. Косинус возрастает на отрезках 2. Косинус убывает на отрезках
Тангенс Тангенсом числа называется отношение синуса этого числа к косинусу этого числа: Тангенсом угла в а радиан называется тангенс числа а. Тангенс - функция числа. Ее область определения - множество всех чисел, у которых косинус не равен нулю, так как никаких других ограничений в определении тангенса нет. И так как косинус равен нулю при Область значений тангенса - множество всех действительных чисел. Период тангенса равен Знак тангенса: тангенс - отношение синуса к косинусу. Значит, он 1. равен нулю, когда синус равен нулю, то есть при 2. положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при 3. отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при Тангенс - функция нечетная. Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых, Вот и получилось, что Значит, тангенс возрастает на каждом участке своей области определения, то есть на всех интервалах вида Котангенс Котангенсом числа называется отношение косинуса этого числа к синусу этого числа: Область значений котангенса - множество всех действительных чисел. Период котангенса равен Знак котангенса: котангенс - отношение косинуса к синусу. Значит, он 1. равен нулю, когда косинус равен нулю, то есть при 2. положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при 3. отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при Котангенс - функция нечетная. Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых, В силу нечетности синуса и четности косинуса, числитель полученной дроби равен Вот и получилось, что
|
||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 1987; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

 . Ведь через каждые
. Ведь через каждые  , где n - любое целое число;
, где n - любое целое число; , где n - любое целое число;
, где n - любое целое число;
 симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их ординаты - синусы - окажутся также противоположными. То есть
симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их ординаты - синусы - окажутся также противоположными. То есть 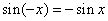 для любого x.
для любого x. , где n - любое целое число.
, где n - любое целое число. , где n - любое целое число.
, где n - любое целое число. при
при  ;
; при
при  .
. , где n - любое целое число;
, где n - любое целое число;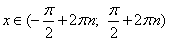 , где n - любое целое число;
, где n - любое целое число; , где n - любое целое число.
, где n - любое целое число. симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их абсциссы - косинусы - окажутся равными. То есть
симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их абсциссы - косинусы - окажутся равными. То есть для любого x.
для любого x. , где n - любое целое число.
, где n - любое целое число. , где n - любое целое число.
, где n - любое целое число.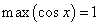 при
при  ;
;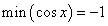 при
при  .
. .
. , где
, где 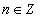 .
. . Ведь если взять любые два допустимые значения x (не равные
. Ведь если взять любые два допустимые значения x (не равные  ), отличающиеся друг от друга на
), отличающиеся друг от друга на 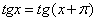 , то есть число
, то есть число  , где а - любое целое число.
, где а - любое целое число. , где а - любое целое число.
, где а - любое целое число. . В силу нечетности синуса и четности косинуса, числитель полученной дроби равен
. В силу нечетности синуса и четности косинуса, числитель полученной дроби равен  , а ее знаменатель равен
, а ее знаменатель равен 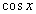 , а значит, сама эта дробь равна
, а значит, сама эта дробь равна  .
. .
. , где а - любое целое число.
, где а - любое целое число. . Котангенсом угла в а радиан называется котангенс числа а. Котангенс - функция числа. Ее область определения - множество всех чисел, у которых синус не равен нулю, так как никаких других ограничений в определении котангенса нет. И так как синус равен нулю при
. Котангенсом угла в а радиан называется котангенс числа а. Котангенс - функция числа. Ее область определения - множество всех чисел, у которых синус не равен нулю, так как никаких других ограничений в определении котангенса нет. И так как синус равен нулю при  , где
, где 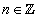
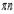 ), отличающиеся друг от друга на
), отличающиеся друг от друга на  , то есть, что число
, то есть, что число 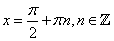 .
. .
.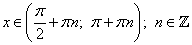 .
. .
. .
. . Котангенс убывает на каждом участке своей области определения, то есть на всех интервалах вида
. Котангенс убывает на каждом участке своей области определения, то есть на всех интервалах вида  .
.



