
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логарифмические уравнения, основные способы решения.Содержание книги
Поиск на нашем сайте
Логарифмическим уравнением называется уравнение, в котором неизвестное (х) и выражения с ним находятся под знаком логарифмической функции. Решение логарифмических уравнений подразумевает, что вы уже знакомы спонятием и видами логарифмов и основными формулами. Самое простое уравнение имеет вид logax = b, где a и b -некоторые числа,x — неизвестное. Следует отметить, что если х будет находиться где-нибудь вне логарифма, например log2х = х-2, то такое уравнение уже называется смешанным и для его решения нужен особый подход. Идеальным случаем является ситуация, когда Вам попадется уравнение, в котором под знаком логарифма находятся только числа, например х+2 = log22. Здесь достаточно знать свойства логарифмов для его решения. Но такая удача случается не часто, поэтому приготовьтесь к более сложным вещам. Но сначала, все-таки, начнём с простых уравнений. Для их решения желательно иметь самое общее представление о логарифме. Рассмотрим логарифмические уравнения вида:
Решение этих уравнений основано на следующей теореме. Теорема 1. Уравнение
Для решения уравнения (1) достаточно решить уравнение
и его решения подставить в систему неравенств
задающую область определения уравнения (1). Корнями уравнения (1) будут только те решения уравнения (3), которые удовлетворяют системе (4), т.е. принадлежат области определения уравнения (1). При решения логарифмических уравнений может произойти расширение области определения (приобретение посторонних корней) или сужение (потеря корней). Поэтому подстановка корней уравнения (3) в систему (4), т.е. проверка решения, обязательна. Пример 1: Решить уравнение Решение:
Оба значения х удовлетворяют условиям системы. Ответ: Рассмотрим уравнения вида:
Их решение основано на следующей теореме Теорема 2: Уравнение (5) равносильно системе
Корнями уравнения (5) будут только те корни уравнения принадлежат области определения, задаваемой условиями Логарифмическое уравнение вида (5) можно решить различными способами. Рассмотрим основные из них. 1. ПОТЕНЦИНИРОВАНИЕ (применение свойств логарифма). 2. ИСПОЛЬЗОВАНИЕ ОПРЕДЕЛЕНИЯ ЛОГАРИФМА ПРИВЕДЕНИЕ К КВАДРАТНОМУ УРАВНЕНИЮ. ЛОГАРИФМИРОВАНИЕ. ПРИВЕДЕНИЕ К ОДНОМУ ОСНОВАНИЮ. 6. ВВЕДЕНИЕ ВСПОМОГАТЕЛЬНОЙ ПЕРЕМЕННОЙ. ГРАФИЧЕСКИЙ СПОСОБ. Многие уравнения, содержащие переменную не только под знаком логарифма или в показателе степени, удобно решать графически. Графически решением уравнения являются абсциссы точек пересечения графиков функций, заданных в уравнении. МЕТОД ПОДБОРА.
|
||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.47.193 (0.006 с.) |

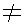 1.
1.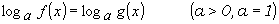 (1)
(1)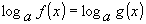 равносильно системе
равносильно системе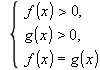 (2)
(2)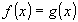 (3)
(3)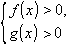 (4),
(4),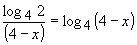




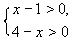

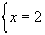

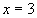
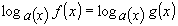 (5)
(5)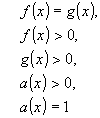 (6)
(6)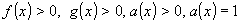 .
.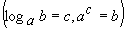 .
.


