
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показательные неравенства. Основные способы решения.Содержание книги
Поиск на нашем сайте
Показательным неравенством называется неравенство, в котором неизвестная содержится только в показателе степени при постоянном основании А, А > 0, A ¹ 1. При решении показательныx неравенств используются следующие утверждения: A.1. Если a > 1, неравенство a f (x) > a g (x) равносильно неравенству f (x) > g (x). Аналогично, a f (x) < a g (x) Û f (x) < g (x). A.2. Если 0 < a < 1, неравенство a f (x) > a g (x) равносильно неравенству f (x) < g (x). Аналогично, a f (x) < a g (x) Û f (x) > g (x). A.3. Неравенство [ h (x)] f (x) > [ h (x)] g (x) равносильно совокупности систем неравенств
Замечание.. Если знак неравенства (1) нестрогий, дополнительно рассматривается и случай
где D (f) (D (g)) означает область определения функции f (g). A.4. Если b ≥ 0, неравенство af (x) < b не имеет решений (следует из свойств показательной функции). A.5. Если b ≤ 0, множеством решений неравенства af (x) > b является x Î D (f). A.6. Если a > 1, b > 0, неравенство af (x) > b равносильно неравенству f (x) > log ab. Аналогично, a f (x) < b Û f (x) < log ab. A.7. Если 0 < a < 1, b > 0, неравенство a f (x) > b равносильно неравенству f (x) < log ab. Аналогично, a f (x) < b Û f (x) > log ab. Логарифм. Свойства логарифмов. Десятичные и натуральные логарифмы. Логарифмом числа B (B > 0) По основанию а (А > 0, А ¹ 1) называют показатель степени, в которую нужно возвести число А, чтобы получить число B:
Формулу (6.1) называют Основным логарифмическим тождеством. Логарифм числа B по основанию 10 называется Десятичным логарифмом И обозначается Логарифм по основанию E (E = 2,71828…) называется Натуральным логарифмом и обозначается Свойства логарифмов Пусть 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) Обобщенные свойства логарифмов Пусть 3*) 4*) 5*) 6*) З а м е ч а н и е 1. Следует различать произведение логарифмов З а м е ч а н и е 2. Степень логарифма может быть записана двумя способами:
Логарифмированием называется операция нахождения логарифма числа или выражения. Основное логарифмическое тождество. Правила действия с логарифмами. Переход к новому основанию.
Показательное уравнение
Итак, логарифмом числа Определение Выражение Натуральный логарифм — это логарифм по основанию e. Обозначается lnx.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.195.219 (0.009 с.) |


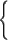
 (6.1)
(6.1)

 Тогда:
Тогда:

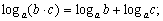


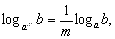






 Тогда и только тогда, когда
Тогда и только тогда, когда 
 тогда и только тогда, когда
тогда и только тогда, когда 
 тогда и только тогда, когда
тогда и только тогда, когда 
 и
и  – выражения с переменной. Тогда:
– выражения с переменной. Тогда: где
где 
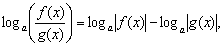 где
где 
 где
где 
 где
где 
 и повторный логарифм
и повторный логарифм 
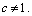
 или
или 
 не имеет решений при
не имеет решений при 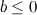 и имеет единственный корень в случае, когда
и имеет единственный корень в случае, когда  . Этот корень называют логарифмом числа
. Этот корень называют логарифмом числа  по основанию
по основанию  и обозначают
и обозначают  , то есть
, то есть
 с учетом того, что
с учетом того, что  называется - основным логарифмическим тождеством.
называется - основным логарифмическим тождеством.


