
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корни натуральной степени и их свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Арифметическим корнем n-ой степени из неотрицательного числа Степень корня – это натуральное число, большее 1.
2. 3. 4. 5. Частные случаи: 1. Если показатель корня целое нечетное число ( В случае нечетного показателя уравнение
Для корня нечетной степени справедливо тождество:
2. Если показатель корня целое четное число ( В случае четного показателя уравнение при и, если Для корня четной степени справедливо тождество:
Для корня четной степени справедливы равенства:
Степенная функция, ее свойства и график. Степенная функция и ее свойства.
Прямая пропорциональность. Прямой пропорциональностью называется функция, заданная формулой у = kxn, где число k называется коэффициентом пропорциональности. Перечислим свойства функции у = kx. Область определения функции — множество всех действительных чисел. y = kx — нечетная функция (f(— х) = k (— х)= — kx = -k(х)).
График (прямая) изображен на рисунке II.1. Рис. II.1. При n=2 получаем функцию y = х2, ее свойства: Функция у —х2. Перечислим свойства функции у = х2. Область определения функции — вся числовая прямая. у = х2— четная функция (f(— х) = (— x)2 = x2 = f (х)). На промежутке [0; + οο) функция возрастает. В самом деле, если 4) На промежутке (- В самом доле, если (-х1)2> (- х2)2, т. е.
Рис. II.2. При n = 3 получаем функцию у = х3, ее свойства: Область определения функции — вся числовая прямая. y = х3 — нечетная функция (f (- х) = (- x)2 = - х3 = - f (x)).
График (кубическая парабола) изображен на рисунке II.3. Рис. II.3. Пусть n— произвольное четное натуральное число, большее двух: n = 4, 6, 8,.... В этом случае функция у = хn обладает теми же свойствами, что и функция у = х2. График такой функции напоминает параболу у = х2, только ветви графика при |n| >1 тем круче идут вверх, чем больше n, а при Пусть n — произвольное нечетное число, большее трех: n = = 5, 7, 9,.... В этом случае функция у = хn обладает теми же свойствами, что и функция у = х3. График такой функции напоминает кубическую параболу (только ветви графика тем круче идут вверх, вниз, чем больше n. Отметим также, что на промежутке (0; 1) график степенной функции у = хn тем медленнее отдаляется от оси х с ростом х, чем больше n. Степенная функция с целым отрицательным показателем. Рассмотрим функцию у = х-n, где n — натуральное число. При n = 1 получаем у = х-n или у =
|
||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 3889; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.125.236 (0.006 с.) |

 называется неотрицательное число, n-я степень которого равна
называется неотрицательное число, n-я степень которого равна  ,
,  ,
, 

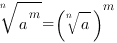


 ), то подкоренное выражение может быть отрицательным.
), то подкоренное выражение может быть отрицательным.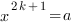
 при любом действительном значении
при любом действительном значении  ВСЕГДА имеет единственный корень:
ВСЕГДА имеет единственный корень: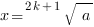 ,
,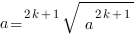 ,
, ), то подкоренное выражение не может быть отрицательным.
), то подкоренное выражение не может быть отрицательным. имеет
имеет единственный корнь
единственный корнь 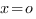




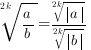
 Степенная функция с натуральным показателем. Функция у = хn, где n — натуральное число, называется степенной функцией с натуральным показателем. При n = 1 получаем функцию у = х, ее свойства:
Степенная функция с натуральным показателем. Функция у = хn, где n — натуральное число, называется степенной функцией с натуральным показателем. При n = 1 получаем функцию у = х, ее свойства: 3) При k > 0 функция возрастает, а при k < 0 убывает на всей числовой прямой.
3) При k > 0 функция возрастает, а при k < 0 убывает на всей числовой прямой. , то
, то 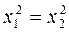 , а это и означает возрастание функции.
, а это и означает возрастание функции. ; 0] функция убывает.
; 0] функция убывает. , а это и означает убывание функции.
, а это и означает убывание функции. Графиком функции y=х2 является парабола. Этот график изображен на рисунке II.2.
Графиком функции y=х2 является парабола. Этот график изображен на рисунке II.2. 3) Функция y = x3 возрастает на всей числовой прямой. График функции y = x3 изображен на рисунке. Он называется кубической параболой.
3) Функция y = x3 возрастает на всей числовой прямой. График функции y = x3 изображен на рисунке. Он называется кубической параболой. тем «теснее прижимаются» к оси х, чем больше n.
тем «теснее прижимаются» к оси х, чем больше n. Свойства этой функции:
Свойства этой функции: График (гипербола) изображен на рисунке II.4.
График (гипербола) изображен на рисунке II.4.


