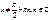Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Арифметический квадратный корень
Определение Арифметическим квадратным корнем из неотрицательного числа a - (
Корнем k –ой степени из a (k - нечетное) называется число, k -ая степень которого равна a.
Квадратное уравнение: ax2 + bx + c = 0
Дискриминант: D = b2 – 4ac
Теорема Виета Приведенное квадратное уравнение: x2 + px + q = 0 x1 + x2 = - p x1 × x2 = q x1+x2 = -b/a x1× x2 = c/a Логарифм Определение Логарифмом числа по b основанию a называется такое число, обозначаемое a - основание логарифма (a > 0, a ¹ 1), b - логарифмическое число (b > 0) Десятичный логарифм: Натуральный логарифм: Формулы
Дроби Сложение Деление с остатком:

Вычитание
Умножение
Деление
Составная дробь Делимость натуральных чисел: Пусть n: m = k, где n, m, k – натуральные числа. Тогда m – делитель числа n, а n – кратно числу m. Число n называется простым, если его делителями являются только единица и само число n. Множество простых чисел: {2; 3; 5; 7; 11; 13;...; 41; 43; 47 и т.д.} Числа n и m называются взаимно простыми, если у них нет общихделителей, кроме единицы. Десятичные числа: Стандартный вид: 317,3 = 3,173× 102 ; 0,00003173 = 3,173× 10-5 Форма записи: 3173 = 3× 1000 + 1× 100 + 7× 10 + 3 Модуль Формулы Определение · ½ x ½ ³ 0 · ½ x - y ½ ³ ½ x ½ - ½ y ½ · ½- x ½=½ x ½ · ½ x × y ½ = ½ x ½ × ½ y ½ · ½ x ½ ³ x
· ½ x: y ½ =½ x ½: ½ y ½ · ½ x + y ½ £ ½ x ½ + ½ y ½ ½ x ½2 = x 2 Неравенства Определения: Неравенством называется выражение вида: a < b (a £ b), a > b (a ³ b)
Основные свойства:
Модуль: уравнения и неравенства 1. 2. 3. 4. 5. Периодическая дробь
Признаки делимости чисел: Проценты Определение: Процентом называется сотая часть от числа. 1%A = 0,01A Основные типы задач на проценты: Сколько процентов составляет число A от числа B? B - 100% A - x% Сложные проценты. Число A увеличилось на 20%, а затем полученное число уменьшили на 25%. Как, в итоге, изменилось исходное число? 1) A1 = (100% + 20%)A = 120%A = 1,2A 2) A2 = (100% - 25%)A1=75%A1 = 0,75A1 = 0,75×1,2A = 0,9A = 90%A 3) A1 – A = 90%A – 100%A = -10%A Þ Ответ: уменьшилось на 10%. Изменение величины. Как изменится время, если скорость движения увеличится на 25%?
Þ Ответ: уменьшится на 20%
Þ Ответ: уменьшится на 20% Среднее арифметическое, геометрическое Среднее арифметическое: Среднее геометрическое: Уравнение движения Пусть Тогда: где Определенный интеграл
Первообразная элементарных функций
Правила вычисления первообразной функции Определение: Функция F(x) называется первообразной для функции f(x), если
Правила вычисления производной функции
Производные элементарных функций
Равносильные уравнения:
Числовые множества:
Тригонометрия
Основные триг. формулы
Формулы суммы функций
Формулы суммы аргументов:
Формулы произведения функций
Формулы половинного аргумента
Формулы двойного аргумента
Формула дополнительного угла
Универсальная подстановка
Свойства тригонометрических функций
Тригонометрические уравнения Косинус:
Уравнения с синусом Частные формулы:
Общая формула:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.242.165 (0.067 с.) |
 ) - называется неотрицательное число, квадрат которого равен a.
) - называется неотрицательное число, квадрат которого равен a.











 , что
, что  .
.
 где e = 2,71828
где e = 2,71828














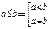











 Правило:
Правило: 





 - уравнение движения материальной точки, где S – путь, t – время движения.
- уравнение движения материальной точки, где S – путь, t – время движения. ,
, – скорость,
– скорость,  - ускорение.
- ускорение.








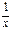






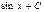


 .
.









 Сложная функция:
Сложная функция:








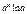

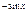


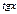



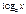











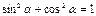 Þ
Þ 


 Þ
Þ 




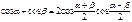









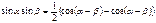




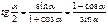



 где
где

 Определение тригонометрических функций
Определение тригонометрических функций