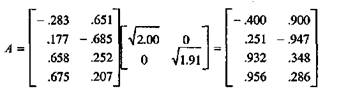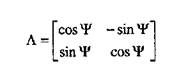Основные уравнения и процедуры факторного анализа

Основные уравнения

Раньше практически во всех учебниках и монографиях по факторному анализу предусматривалось объяснение того, как проводить основные вычисления «вручную» или посредством простейшего счетного устройства (арифмометра или калькулятора). Сегодня в связи со сложностью и большим объемом вычислений, необходимых для построения матрицы взаимосвязей, выделения факторов и их вращения, наверное, не осталось ни одного человека, который при проведении факторного анализа не использовал бы мощных компьютеров и соответствующих программ.

Поэтому мы сосредоточим внимание на том, какие наиболее существенные матрицы (массивы данных) можно получить в ходе факторного анализа, как они связаны друг с другом и как их можно использовать для интерпретации данных. Все необходимые вычисления можно сделать с помощью любой компьютерной программы (например, SPSS или STADIA).

В табл. 1 приведен список наиболее важных матриц для методов главных компонент и факторного анализа. Этот список содержит в основном матрицы взаимосвязей (между переменными, между факторами, между переменными и факторами), стандартизированных значений (по переменным и по факторам), регрессионных весов (для расчета факторных значений с помощью значений по переменным), а также матрицы факторных отображений взаимосвязей между факторами и переменными после косоугольного вращения. В табл. 1 приводятся также матрицы собственных чисел и соответствующих им собственных векторов. Собственные числа (собственные значения) и собственные вектора описываются ввиду их значимости для выделения факторов, употребления в этой связи большого количества специальных терминов, а также тесной связи собственных чисел и дисперсии в статистических исследованиях.

Таблица 1

Матрицы, наиболее часто используемые в факторном анализе

Обозначение	Название	Размер	Описание
R	Матрица взаимосвязей	p x p	Взаимосвязи между переменными
D	Матрица нестандартизированных данных	N x p	Первичные данные — нестандартизированные значения наблюдений по первичным переменным
Z	Матрица стандартизированных данных	N x p	Стандартизованные значения наблюдений по первичным переменным
F	Матрица значений факторов	N x f	Стандартизированные значения наблюдений по факторам
А	Матрица факторных нагрузок Матрица факторного отображения	p x f	Коэффициенты регрессии для общих факторов при условии, что наблюдаемые переменные являются линейной комбинацией факторов. В случае ортогонального вращения — взаимосвязи между переменными и факторами
В	Матрица коэффициентов значений факторов	p x f	Коэффициенты регрессии для вычисления значений факторов с помощью значений переменных
S	Структурная матрица	p x f	Взаимосвязи между переменными и факторами
Ф	Матрица корреляций факторов	f x f	Корреляции между факторами
L	Матрица собственных значений (диагональная)	f x f	Собственные значения (характеристические, латентные корни); каждому фактору соответствует одно собственное число
V	Матрица собственных векторов	f x f	Собственные (характеристические) вектора; каждому собственному числу соответствует один собственный вектор

Примечание. При указании размера дается количество рядов х количество столбцов: р — количество переменных, N — количество наблюдений, f — количество факторов или компонент. Если матрица взаимосвязей R не вырождена и имеет ранг равный р, то тогда фактически выделяется р собственных чисел и собственных векторов, а не f. Однако интерес представляют только f из них. Поэтому оставшиеся p - f не показываются.

К матрицам S и Ф применяется только косоугольное вращение, к остальным — ортогональное и косоугольное.

 

Набор данных, подготовленных для факторного анализа, состоит из результатов измерений (опроса) большого количества испытуемых (респондентов) по определенным шкалам (переменными). В табл. 2 приводится массив данных, который условно можно считать удовлетворяющим требованиям факторного анализа.

Пяти респондентам, обратившимся в туристическое агентство с целью приобрести путевку на морской курорт, были заданы вопросы о значимости для них четырех условий (переменных) выбора места летнего отдыха. Этими условиями-переменными были: стоимость путевки, комфортабельность комплекса, температура воздуха, температура воды. Чем большей, с точки зрения респондента, значимостью обладало для него то или иное условие, тем большее значение он ему приписывал. Исследовательская задача состояла в изучении модели взаимосвязи между переменными и выявлении глубинных причин, обусловливающих выбор курорта. (Пример, конечно же, предельно упрощен в иллюстративно-учебных целях, и его не следует рассматривать всерьез в содержательном аспекте.)

Матрица взаимосвязей (табл. 2) была вычислена как корреляционная. Обратите внимание на структуру взаимосвязей в ней, выделенную вертикальными и горизонтальными линиями. Высокие корреляции в верхнем левом и нижнем правом квадрантах показывают, что оценки по стоимости путевки и комфортабельности комплекса взаимосвязаны, также как и оценки по температуре воздуха и температуре воды. Два других квадранта показывают, что температура воздуха и комфортабельность комплекса связаны между собой, также как и комфортабельность комплекса и температура воды.

Попробуем теперь с помощью факторного анализа обнаружить эту структуру корреляций, легко замечаемую невооруженным глазом в маленькой корреляционной матрице (в большой матрице это очень непросто сделать).

 

Таблица 2

Данные для факторного анализа (учебный пример)

Туристы	Переменные
Стоимость путевки	Уровень комфорта	Температура воздуха	Температура воды
T1
Т2
Т3
Т4
Т5

Корреляционная матрица

	Стоимость путевки	Уровень комфорта	Температура воздуха	Температура воды
Стоимость путевки	1,000	-0,953	-0,055	-0,130
Уровень комфорта	-0,953	1,000	-,091	-0,036
Температура воздуха	-0,055	-0,091	1,000	0,990
Температура воды	-0,130	-0,036	0,990	1,000

 

Факторизация

Важная теорема из матричной алгебры гласит, что матрицы, удовлетворяющие определенным условиям, могут быть диагонализированы, т.е. преобразованы в матрицу, на главной диагонали которой стоят числа, а на всех остальных позициях — нули. Матрицы взаимосвязей относятся именно к типу диагонализируемых матриц. Преобразование проводится по формуле:

L=V’RV (6)

т.е. диагонализация матрицы R выполняется умножением ее сначала (слева) на транспонированную матрицу V, обозначаемую V’, а потом (справа) на саму матрицу V.

Столбцы в матрице V называются собственными векторами, а величины на главной диагонали матрицы L, — собственными числами. Первый собственный вектор соответствует первому собственному числу и т.д. (подробнее об этом см. в Приложении 1).

В связи с тем, что в приведенном примере рассматриваются четыре переменные, мы получаем четыре собственные величины с соответствующими им собственными векторами. Но поскольку целью факторного анализа является обобщение матрицы взаимосвязей посредством как можно меньшего количества факторов и каждая собственная величина соответствует разным потенциально возможным факторам, обычно принимаются в расчет только факторы с большими собственными величинами. При «хорошем» факторном решении матрица вычисленных взаимосвязей, полученная с помощью этого ограниченного набора факторов, практически дублирует матрицу взаимосвязей.

В нашем примере, когда на количество факторов не накладываются никакие ограничения, собственные величины 2.02, 1.94,.04 и.00 вычисляются для каждого из четырех возможных факторов. Только для первых двух факторов собственные значения достаточно велики, чтобы стать предметом дальнейшего рассмотрения. Поэтому выполняется повторное выделение только первых двух факторов. Они имеют собственные величины 2.00 и 1.91 соответственно, как это указано в табл. 3. Используя уравнение (6) и вставив значения из приведенного примера, получаем:

(Все величины, вычисленные на компьютере, совпадают; расчеты, выполненные «вручную», могут отличаться в связи с неточностями округления.)

Умножение слева матрицы собственных векторов на транспонированную ей дает единичную матрицу Е (с единицами на главной диагонали и остальными нулями). Поэтому можно сказать, что преобразование матрицы взаимосвязей по формуле (6) не изменяет ее саму, а лишь преобразует к более удобному для анализа виду:

V’ V=E (7)

Например:

Таблица 3

Собственные векторы и соответствующие собственные числа для рассматриваемого учебного примера

Собственный вектор 1	Собственный вектор 2
-.283	.651
.177	-.685
.658	.252
.675	.207
Собственное значение 1	Собственное значение 2
2.00	1.91

 

Поскольку корреляционная матрица диагонализируема, то для получения результатов факторного анализа к ней можно применять матричную алгебру собственных векторов и собственных величин (см. Приложение 1). Если матрица диагонализируема, то вся существенная информация о факторной структуре содержится в ее диагональной форме. В факторном анализе собственные числа соответствуют дисперсии, объясняемой факторами. Фактор с наибольшей собственной величиной объясняет наибольшую дисперсию и т.д., пока не доходит до факторов с небольшими или отрицательными собственными величинами, которые обычно не учитываются при анализе. Расчеты собственных величин и собственных векторов весьма трудоемки, и умение их вычислять не является крайней необходимостью для психолога, осваивающего факторный анализ в своих практических целях. Однако знакомство с этой процедурой не повредит, поэтому в Приложении 1 мы даем в качестве примера вычисления собственных чисел и собственных векторов на маленькой матрице.

Для нахождения собственных величин квадратной матрицы р х р необходимо найти корни многочлена степени р, а для нахождения собственных векторов — решить р уравнений с р неизвестными с дополнительными побочными ограничениями, что для р>3 редко выполняется вручную. Как только найдены собственные вектора и собственные величины, оставшаяся часть факторного анализа (или метода главных компонент) становится более или менее ясной (см. уравнения 8—11).

Уравнение (6) может быть представлено в виде: R=V’LV, (8)

т.е. матрицу взаимосвязей можно рассматривать как произведение трех матриц — матрицы собственных величин, матрицы соответствующих собственных векторов и транспонированной к ней.

После преобразования матрицу собственных величин L можно представить следующим образом:

L=ÖLÖL (9)

и следовательно: R=VÖLÖL V’ (10)

или (что то же самое): R=(VÖL)(ÖL V’)

Обозначим: A=(VÖL), а А’=(ÖL V’), тогда R=AA’ (11)

т.е. матрица взаимосвязей также может быть представлена как произведение двух матриц, каждая из которых есть комбинация собственных векторов и квадратных корней из собственных величин.

Уравнение (11) часто называют фундаментальным уравнением факторного анализа[6]. Оно выражает утверждение о том, что матрица взаимосвязей — это произведение матрицы факторных нагрузок (А) и транспонированной к ней.

Уравнения (10) и (11) также показывают, что значительная доля вычислений в методах факторного анализа и главных компонент заключается в определении собственных величин и собственных векторов. Как только они становятся известны, факторная матрица до поворота получается путем прямого матричного умножения:

A=VÖL (12)

В нашем примере:

Матрица факторных нагрузок является матрицей взаимосвязей (интерпретируемых как коэффициенты корреляций) между факторами и переменными. Первый столбец — это корреляции между первым фактором и каждой переменной по очереди: стоимость путевки (-.400), комфортабельность комплекса (.251), температура воздуха (.932), температура воды (.956). Второй столбец — это корреляции между вторым фактором и каждой переменной: стоимость путевки (.900), комфортабельность комплекса (—.947), температура воздуха (.348), температура воды (.286). Фактор интерпретируется на основе сильно связанных с ним (т.е. имеющих по нему высокие нагрузки) переменных. Так, первый фактор главным образом «климатический» (температура воздуха и воды), в то время как второй «экономический» (стоимость путевки и комфортабельность комплекса).

Интерпретируя эти факторы, следует обратить внимание на то, что переменные, имеющие высокие нагрузки по первому фактору (температура воздуха и температура воды), взаимосвязаны положительно, тогда как переменные, имеющие высокие нагрузки по второму фактору (стоимость путевки и комфортабельность комплекса), взаимосвязаны отрицательно (от дешевого курорта нельзя ожидать большой комфортабельности). Первый фактор называется униполярным (все переменные сгруппированы на одном полюсе), а второй — биполярным (переменные распались на две противоположные по смыслу группы — два полюса). Переменные, имеющие факторные нагрузки со знаком «плюс», образуют положительный полюс, а со знаком «минус» — отрицательный. При этом названия полюсов «положительный» и «отрицательный» при интерпретации фактора не имеют оценочного смысла «плохой» и «хороший». Выбор знака происходит во время вычислений случайным образом. Замена всех знаков на противоположные (всех плюсов на минусы, а всех минусов на плюсы) решения не меняет. Анализ знаков необходим только для идентификации групп (что чему противопоставлено). С таким же успехом один полюс можно называть правым, другой левым. В нашем примере переменная стоимость путевки оказалась на положительном (правом) полюсе, ей противопоставлена переменная комфортабельность комплекса на отрицательном (левом) полюсе. И этот фактор можно проинтерпретировать (назвать) как «Экономичность о Комфортность». Респонденты, для которых проблема экономии существенна, оказались справа — получили факторные значения со знаком «плюс». При выборе курорта они более ориентируются на его дешевизну и менее — на комфортабельность. Респонденты, не экономящие на отдыхе (цена путевки их мало волнует) и желающие отдохнуть прежде всего в комфортных условиях, оказались слева — получили факторные значения со знаком «минус».

Однако следует иметь в виду, что все переменные в значительной степени коррелируют с обоими факторами. В рамках этого простого примера интерпретация очевидна, но в случае реальных данных не все так просто. Обычно фактор легче интерпретируется, если с ним сильно взаимосвязана только небольшая часть переменных, а остальные — нет.

Ортогональное вращение

Вращение обычно применяется после выделения факторов для максимизации высоких корреляций и минимизации низких. Существуют многочисленные методы вращения, но чаще всего используется поворот варимакс, представляющий собой процедуру максимизации дисперсии. Этот поворот максимизирует дисперсии факторных нагрузок, делая высокие нагрузки выше, а низкие ниже дня каждого из факторов. Эта цель достигается с помощью матрицы преобразования Л:

А до поворота Л=А после поворота,

(13)

т.е. матрица факторных нагрузок до поворота умножается на матрицу преобразования и в результате получается матрица факторных нагрузок после поворота. В нашем примере:

Сравните матрицы до и после поворота. Обратите внимание, что у матрицы после поворота низкие факторные ни грузки ниже, а высокие выше, чем у матрицы до поворота. Подчеркнутая разница нагрузок облегчает интерпретацию фактора, позволяет однозначно выбрать сильно взаимосвязанные с ним переменные.

Элементы матрицы преобразования имеют специальную геометрическую интерпретацию:

(14)

Матрица преобразования — это матрица синусов и косинусов угла ψ, на который выполняется поворот. (Отсюда и название преобразования — поворот, потому что с геометрической точки зрения происходит поворот осей вокруг начала координат факторного пространства.) В нашем примере этот угол составляет примерно 19 градусов: cos19°=.946 и sin19°=.325. Геометрически это соответствует повороту факторных осей на 19 градусов вокруг начала координат. (Более подробно о геометрических аспектах вращения см. далее.)