Критерии оценки качества вращения и простоты полученной структуры

Определившись с количеством значимых факторов, исследователь оказывается перед выбором типа вращения. На первый взгляд, во многих случаях факторного анализа косоугольное вращение кажется более подходящим, чем ортогональное, поскольку ситуация, в которой предполагается, что факторы каким-то образом взаимосвязаны друг с другом, выглядит более соответствующей реальности. Однако описание результатов косоугольного вращения включает анализ матриц факторного отображения и корреляции факторов, тогда как при ортогональном вращении выдается только матрица факторных нагрузок. Иными словами, результаты ортогонального вращения гораздо легче анализировать и интерпретировать. Кроме того, ортогональное вращение дает неоспоримые преимущества для использования факторных значений или подобных им величин в качестве зависимых или независимых переменных в других аналитических процедурах или же при сравнении различных факторных структур.

Возможно, наилучший способ выбора между ортогональным и косоугольным вращением — это выполнение косоугольного вращения с желаемым количеством факторов и анализ корреляций между факторами. Если необходимо найти соответствие с исходными данными для вычисления сильно взаимосвязанных между собой факторов, в программах SPSS, SYSTAT, BMDP и SAS по умолчанию выполняется косоугольное вращение. Однако в том случае, если имеющиеся данные не задают коррелирующих факторов, решение (автоматически) вычисляется как ортогональное.

Если в корреляционной матрице все коэффициенты корреляции превышают 0,32 и не менее 10% объясняемой факторами дисперсии объясняется именно наложением факторов, то при отсутствии каких-либо серьезных причин для проведения ортогонального вращения можно пользоваться косоугольным вращением. К серьезным причинам относятся: желание сравнить различные факторные структуры; необходимость использовать ортогональные факторы в других аналитических процедурах; наличие теоретически обоснованной модели, базирующейся на ортогональном вращении.

Определившись с типом вращения (ортогональное или косоугольное), можно воспользоваться различными способами оценки соответствия решения, полученного после вращения, начальным экспериментальным данным. Наиболее простой способ — сравнить структуры взаимосвязей в матрице взаимосвязей с полученными после вращения факторами. Удалось ли в полученном после вращения решении воспроизвести эти структуры? Имеют ли сильно взаимосвязанные между собой переменные высокие факторные нагрузки по одним и тем же факторам? Насколько высоки факторные нагрузки у маркерных переменных по тем факторам, которые они должны предсказывать (соответствовать, определять) согласно гипотетической модели?

Другой критерий правильности выбранного вращения — простота структуры (Thurstone, 1961). Простая структура имеет не слишком сильно взаимосвязанные между собой факторы. Несколько переменных сильно взаимосвязаны с каждым фактором и только один фактор сильно взаимосвязан с каждой переменной. Другими словами, столбцы матрицы факторных нагрузок Л, определяющие факторы по отношению к переменным, имеют несколько высоких и много низких значений, тогда как строки матрицы А, определяющие переменные по отношению к факторам, имеют по одному высокому значению. Строки с более чем одной высокой факторной нагрузкой соответствуют переменным, считающимся сложными в связи с тем, что они отражают влияние более чем одного фактора. Обычно следует избегать сложных переменных, поскольку они затрудняют интерпретацию факторов.

Адекватность вращения также можно оценить с помощью графиков, изображающих факторные оси и переменные в координатах этих осей (координата по факторной оси для каждой переменной равна факторной нагрузке этой переменной по фактору, соответствующему этой оси). При этом следует обращать внимание на степень удаленности точек-переменных от начала координат, на скопления точек и на характер расположения этих скоплений. (В англоязычных программах эти графики называются «component plot» и выполняются с помощью команды «Plot».) Расстояние от точки-переменной до начала координат соответствует факторным нагрузкам: переменные, высоко коррелирующие с фактором, находятся далеко по оси этого фактора (имеют большую по абсолютной величине координату). В идеале каждая переменная должна находиться далеко от начала координат по оси какого-либо фактора и лежать близко к этой оси (иметь маленькие координаты по всем остальным осям). Скопление точек-переменных показывает, насколько четко определен фактор. Большинство исследователей предпочитает иметь следующую картинку: на конце каждой оси имеется скопление точек, близко лежащих к самой этой оси. Распределение точек вдоль всей оси указывает, что соответствующий фактор определен нечетко, в то время как скопление точек между различными осями указывает на наличие другого фактора или на необходимость косоугольного вращения. Характер расположения скопления после ортогонального вращения может также указывать на необходимость косоугольного вращения. Если после ортогонального вращения образуются скопления точек, лежащие между осями факторов, и угол между скоплениями по отношению к началу координат не равен 90 градусам, тогда лучшее соответствие этим скоплениям обеспечивается неортогональными осями. Косоугольное вращение может выявить существенные корреляции между факторами. Некоторые из этих взаимосвязей изображены на рис. 3.

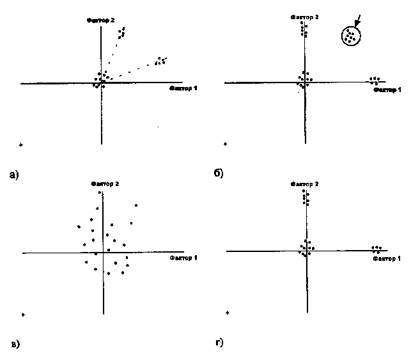
Рис. 3. Графическое представление факторных нагрузок переменных, полученных после ортогонального вращения, в плоскости двух факторов показывает: а) необходимость косоугольного вращения; б) наличие еще одного фактора; в) отсутствие структуры данных; г) наличие простой структуры