
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет сооружений методом конечных элементовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Современная вычислительная техника позволяет проводить расчеты сооружений с более подробным описанием их внутренней структуры и с более точным учетом действующих нагрузок. Для этого разработаны специальные методы расчета, среди которых наибольшее распространение получил метод конечных элементов (МКЭ). Понятие о методе конечных элементов Метод конечных элементов – это метод расчета сооружений, основанный на рассмотрении сооружения как совокупности типовых элементов, называемых конечными элементами (КЭ). В дискретном методе мы рассмотрели три типовых стержневых элементов, которые используются и в МКЭ как конечные элементы. Например, элемент 3-его типа в МКЭ называется ферменным (рис. 14.1 а), а 1-го типа – плоским стержневым конечным элементом (рис. 14.1 б). При расчете пространственных рам используется КЭ бруса (рис. 14.1 в). В расчетах плоских тел (плит или пластин) используются треугольный (рис. 14.1 г) или четырехугольный (рис. 14.1 д) конечные элементы. При расчете пространственных сооружений могут использоваться призменный КЭ (рис. 14.1 е) или тетраэдальный КЭ (рис. 14.1 ж) и др. Для расчета различных сооружений разработано множество других КЭ.
Рис. 14.1 МКЭ – дискретный метод. В этом методе сооружение делится на определенное число КЭ, соединенных между собой в узлах конечно-элементной модели. А нагрузка, действующая на сооружение, переносится в узлы. Это позволяет определять НДС сооружения через узловые усилия и перемещения конечно-элементной модели. Как мы знаем, можно выбирать разные расчетные схемы сооружения. Но и в пределах одной расчетной схемы можно выбирать разные расчетные модели по МКЭ, потому что сооружение можно разбить не только на разное количество однотипных КЭ, но и представить его как комбинацию различных типов КЭ. С другой стороны, при расчете сооружения могут быть реализованы различные варианты МКЭ в формах метода сил, метода перемещений и смешанного метода. В настоящее время широкое распространение получил МКЭ в форме метода перемещений. Вариационные основы МКЭ При решении многих задач статики, динамики и устойчивости сооружений определяется их полная потенциальная энергия U: U = W – V. (1) Здесь W – работа внешних сил, V – работа внутренних сил. Обычно все они представляются в виде функций, зависящих от перемещений, деформаций, напряжений элементов расчетной модели сооружения.
Исследование этого выражения позволяет выявить важные законы механики, называемые принципами. Например, в теоретической механике известен принцип Лагранжа-Дирихле: для того чтобы механическая система находилась в равновесии, ее полная потенциальная энергия должна быть постоянной. Из этого принципа следует, что приращение полной потенциальной энергии системы, находящейся в равновесии, должно равняться нулю:
Вычисление приращения функции обычно заменяется вычислением его приближенного значения − дифференциала. В этом случае получается вариационное уравнение Лагранжа
где символ С учетом (1) вариационное уравнение Лагранжа принимает вид
Оно формулируется как принцип Лагранжа: вариация работы внутренних сил равна вариации работы внешних сил. Принцип Лагранжа используется для сведения континуальной задачи расчета сооружений к дискретной задаче путем аппроксимации (приближенного определения) непрерывных полей перемещений, деформаций, напряжений внутри конечного элемента по его узловым перемещениям. В строительной механике используются и другие вариационные принципы, аналогичные принципу Лагранжа, такие как принципы Кастильяно, Рейсснера, Ху-Вашицу и др. Однако мы воспользуемся только вариационным принципом Лагранжа как основой варианта МКЭ в форме метода перемещений. Аппроксимация КЭ Имея КЭ разного типа, при выборе конечно-элементной модели сооружения можно вводить узлы с разным числом степеней свободы. Например, в плоской системе могут рассматриваться узлы как с тремя степенями свободы (рис. 14.2 а), так и с двумя (рис. 14.2 б) или даже с одной степенью свободы. В первом случае учитываются два линейных (поступательных) и одно угловое перемещение узла, во втором – два линейных перемещения, а в третьем − лишь одно поступательное перемещение. В пространственной системе узлы могут иметь шесть (рис. 14.2 в) или три степени свободы (рис. 14.2 г).
Рис. 14.2 Для упорядочения степеней свободы и соответствующих перемещений узлов КЭ все они нумеруются в определенном порядке и собираются в общий вектор перемещений u. Чтобы воспользоваться принципом Лагранжа, вводятся так называемые координатные функции, аппроксимирующие непрерывное поле перемещений внутри КЭ через перемещения ее узлов:
Здесь В качестве простейшего примера рассмотрим ферменный КЭ с узлами i и j (рис. 14.3 а) в местной системе координат
Рис. 14.3 Перемещения внутренних точек
Запишем его в матричной форме:
где Подставив
С другой стороны,
Тогда их можно записать в матричной форме
и представить как матричное уравнение
связывающее вектор узловых перемещений Определим вектор
Тогда
или
Входящая сюда матрица H По аналогии с перемещениями поле внутренних усилий
Например, для рассмотренного КЭ имеем
Матрица жесткости КЭ Известные в механике геометрические и физические соотношения для континуальных систем можно записать в виде, аналогичном рассмотренным ранее уравнениям дискретного подхода. Например, для дискретной системы: для континуальной системы: Здесь При рассмотрении конечного элемента как континуальной системы принцип Лагранжа
где левая и правая части представляют возможные работы внутренних и внешних сил, а интегрирование ведется по объему КЭ V. После этого осуществляется переход к дискретной модели КЭ с использованием матрицы форм H. Тогда после ряда преобразований получается матричное уравнение, связывающее вектор узловых перемещений u с вектором узловых усилий P КЭ:
в которой симметричная квадратная матрица
называется матрицей жесткости конечного элемента. Физический смысл элемента kij этой матрицы – это реакция (реактивная сила), возникающая в i -ом направлении отзаданного единичного перемещения в j -ом направлении. К примеру, для рассмотренного ферменного КЭ, находящегося в одноосном напряженном состоянии, геометрическое уравнение будет
Для определения матрицы жесткости КЭ вычислим:
Интегрирование по объему V сводится к интегрированию по длине l КЭ, т.к.
При рассмотрении прямоугольного КЭ толщиной t и размерами 2a и 2b с четырьмя узлами i, j, k, m и восемью узловыми перемещениями (рис. 14.4), матрица жесткости будет иметь размеры 8´8.
Рис. 14.4 Для краткости записи матрицу жесткости этого КЭ можно представить в блочной форме с 16 блоками одинаковой размерности 2´2:
Здесь μ – коэффициент Пуассона. Элементы каждого блока матрицы K определяются по разным формулам. Например,
В о п р о с ы 1. Какой из подходов механики реализуется в МКЭ? 2. Какие основные типы КЭ используются в МКЭ? 3. Как формулируется принцип Лагранжа? 4. Для чего нужны координатные функции и матрицы форм? 5. Что такое функция формы? 6. Как определяется матрица жесткости КЭ? 7. Какой физический смысл имеют элементы матрицы жесткости? Л е к ц и я 15
|
|||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.202.216 (0.012 с.) |


 .
. ,
, означает вариацию, вычисление которого схоже с вычислением дифференциала функции. Это уравнение позволяет свести задачу определения НДС сооружения к отысканию экстремума полной потенциальной энергии.
означает вариацию, вычисление которого схоже с вычислением дифференциала функции. Это уравнение позволяет свести задачу определения НДС сооружения к отысканию экстремума полной потенциальной энергии. .
.
 .
.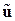 – вектор перемещений внутренних точек КЭ, C – матрица координатных функций,
– вектор перемещений внутренних точек КЭ, C – матрица координатных функций, 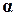 – вектор коэффициентов. Элементы матрицы C выбираются в виде полиномов, непрерывных внутри КЭ. Если в полиноме учитывается минимальное число членов, то такой КЭ называется симплекс-элементом. При учете большего числа членов полинома КЭ называется комплекс-элементом.
– вектор коэффициентов. Элементы матрицы C выбираются в виде полиномов, непрерывных внутри КЭ. Если в полиноме учитывается минимальное число членов, то такой КЭ называется симплекс-элементом. При учете большего числа членов полинома КЭ называется комплекс-элементом. . Его узлы имеют по одной поступательной степени свободы по оси
. Его узлы имеют по одной поступательной степени свободы по оси 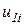 и
и  . Допустим, что в узлах КЭ приложены силы
. Допустим, что в узлах КЭ приложены силы  и
и  (рис. 14.3 б).
(рис. 14.3 б).
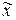 элемента будем аппроксимировать полиномом первой степени
элемента будем аппроксимировать полиномом первой степени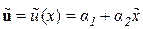 .
. ,
, называется матрицей координатных функций, а
называется матрицей координатных функций, а  является вектором неизвестных коэффициентов.
является вектором неизвестных коэффициентов. и
и  в наш полином, получим два равенства:
в наш полином, получим два равенства: ,
,  .
. и
и  (рис. 14.3 б). Учитывая их, предыдущие равенства перепишем так:
(рис. 14.3 б). Учитывая их, предыдущие равенства перепишем так: ,
,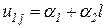 .
.
 ,
,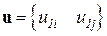 и вектор координат
и вектор координат  через представленную выше матрицу
через представленную выше матрицу  .
. .
.
 .
. называется матрицей форм. Она позволяет аппроксимировать поле перемещений внутренних точек КЭ через перемещения узлов.
называется матрицей форм. Она позволяет аппроксимировать поле перемещений внутренних точек КЭ через перемещения узлов. в КЭ можно аппроксимировать через вектор узловых сил
в КЭ можно аппроксимировать через вектор узловых сил  по формуле
по формуле .
. .
. ,
,  ,
,  ,
,  .
. и
и  – вектора деформаций и напряжений, а
– вектора деформаций и напряжений, а  и
и  – матрицы равновесия и податливости континуальной системы. В отличие от дискретного подхода, уравнения континуального подхода удовлетворяются во всех точках системы.
– матрицы равновесия и податливости континуальной системы. В отличие от дискретного подхода, уравнения континуального подхода удовлетворяются во всех точках системы. ,
, ,
,
 . Сравнив его с матричным уравнением
. Сравнив его с матричным уравнением  . Из уравнения связи между деформацией и напряжением
. Из уравнения связи между деформацией и напряжением  видно, что матрица податливости будет
видно, что матрица податливости будет  .
. ,
,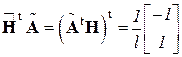 ,
,  .
. (F − площадь сечения КЭ). Тогда
(F − площадь сечения КЭ). Тогда .
.
 .
. .
.


