
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Объединение конечных элементов
Пусть в расчетной модели сооружения имеется m КЭ и n узлов, а вектора ее перемещений и узловых нагрузок определены так:
После построения матриц жесткостей всех конечных элементов Вначале матрицы жесткости всех КЭов собираются в единую диаго-нальную матрицу
Они еще не учитывают связи между соседними конечными элементами в узлах их примыкания. Для объединения КЭов в единую систему используется энергетический принцип: энергия конечно-элементной модели системы равняется сумме энергий всех ее КЭ. В этом случае матрица жесткости объединенной системы будет определяться по формуле
где Г – объединяющая матрица. Элементы этой матрицы состоят только из нулей и единиц, а отдельные ее блоки соответствуют узлам КЭ и строятся по принципу: если КЭ содержит данный узел, то записывается единичная матрица, если нет – нулевая матрица. А соответствующие узловые нагрузки будут объединяться по формуле
Однако получение матрицы жесткости K и вектора нагрузки P таким способом требует больших вычислительных затрат. Задача упрощается, если составить так называемую матрицу индексов, определяющую соответствие номеров узловых перемещений КЭов узловым перемещениям всей модели. Тогда матрицу жесткости K можно получать рассылкой в ее блоки отдельных блоков матриц жесткостей КЭов по информации, заключенной в матрице индексов. При этом рассылка идет с суммированием рассылаемого блока матрицы жесткости КЭ с имеющимся блоком в матрице K. Такой метод называется методом сложения жесткостей. Вектор узловой нагрузки P формируется аналогично. В результате этих действий формируется разрешающее уравнение МКЭ, по виду совпадающее с уравнением МКЭ для отдельного КЭ: Ku=P. Но уже здесь K и P − матрица жесткости и вектор нагрузки всей системы. Матрицу K часто называют глобальной матрицей жесткости. Учет граничных условий Разрешающее уравнение МКЭ нельзя сразу решить относительно перемещений u. Причина в том, что при его составлении не учтены граничные условия закрепления сооружения в опорах. Поэтому матрица жесткости K является вырожденной (т.е. ее определитель равняется нулю). Чтобы выйти из положения, вектор перемещений приходится делить на две части – на перемещения по закрепленным (з) и незакрепленным (н) направлениям:
Так как опоры сооружения обычно бывают достаточно жесткими, их перемещения можно принять равными нулю ( Поэтому используется другой прием: все элементы строк и столбцов матрицы жесткости, соответствующие закреплениям, приравниваются нулю, и лишь вместо их диагональных элементов ставятся единицы. В таком случае разрешающее уравнение упрощается без нарушения ее структуры и принимает вид:
Здесь E − единичная матрица,
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.201.71 (0.006 с.) |
 ,
, .
. и определения векторов узловых нагрузок
и определения векторов узловых нагрузок  в общей системе координат следует сформировать матрицу жесткости и вектор нагрузки всего сооружения. Это можно проделать так.
в общей системе координат следует сформировать матрицу жесткости и вектор нагрузки всего сооружения. Это можно проделать так. , а вектора узловых нагрузок − в единый вектор
, а вектора узловых нагрузок − в единый вектор  :
: ,
,  .
. ,
, .
. .
. ), а нагрузку, приходящуюся на опоры, не учитывать. В таком случае разрешающее уравнение преобразуется в уравнение меньшего размера. Однако такая процедура существенно меняет структуру матрицы жесткости K и усложняет дальнейшее решение.
), а нагрузку, приходящуюся на опоры, не учитывать. В таком случае разрешающее уравнение преобразуется в уравнение меньшего размера. Однако такая процедура существенно меняет структуру матрицы жесткости K и усложняет дальнейшее решение. .
.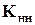 и
и  − блоки матрицы жесткости и вектора нагрузки, соответствующие незакрепленным направлениям.
− блоки матрицы жесткости и вектора нагрузки, соответствующие незакрепленным направлениям.


