
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о статически неопределимых системах
Статически неопределимой называется система, внутренние усилия которой нельзя определить только из уравнений статики (равновесия). Статически неопределимые системы (СНС) отличаются от статически определимых рядом свойств: 1. Они надежнее, разрушение некоторых элементов не всегда приводит к разрушению всей системы. 2. Они выдерживают бо́льшую нагрузку. 3. У них деформации меньше. 4. Изменение температуры, смещение опор, неточность изготовления элементов вызывают дополнительные усилия. 5. Внутренние усилия зависят от физических и геометрических характеристик элементов. У статически неопределимых систем есть так называемые «лишние» связи, число которых называется степенью статической неопределимости. Степень статической неопределимости n простой системы определяется из дискового аналога по следующей формуле:
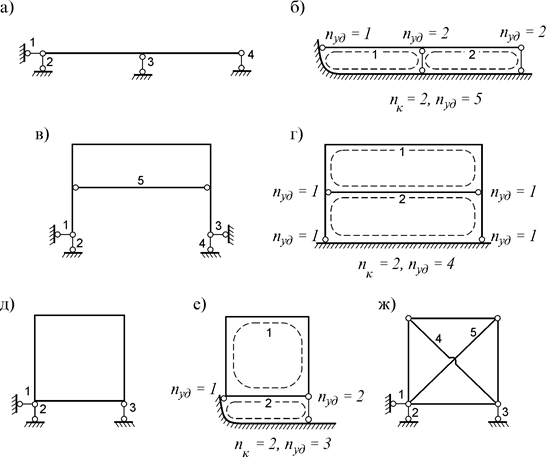
Например, степени статической неопределимости балки (рис. 7.1 а) и рамы (рис. 7.1 в) будут: n=2·0+0+4–3·1=1 и n=2·0+1+4–3·1=2. Использование этой формулы при расчете сложных рам затруднительно. Поэтому можно применить другой подход, вводя два понятия: 1) замкнутый контур – замкнутая цепь из элементов и связей системы; 2) удалённая связь – связь замкнутого контура, исключенная из жесткого соединения элементов (см. рис. 7.1 б, г, е).
Рис. 7.1 Степень статической неопределимости сплошного замкнутого контура равняется трем. Поэтому степень статической неопределимости системы из nк замкнутых контуров, из которых удалены nуд связей, будет n=3nк – nуд. При использовании этой формулы для балки (рис. 7.1 а) и рам (рис. 7.1 в, д) в этих системах необходимо определить общее число замкнутых контуров nк и удаленных связей nуд (рис. 7.4 б, г, е). Тогда − для балки: n=3×2–5=1; − для рам: n=3×2–4=2, n=3×2–4=2. Степень статической неопределимости фермы определяется по формуле n= nС+ n Например, для фермы (рис. 7.1 ж): n=6+3–2×4=1. Выбор основной системы Расчет статически неопределимой системы начинается с превращения ее в статически определимую. Для этого необходимо исключить лишние связи и заменить их реакции неизвестными силами. Полученная система называется основной системой (ОС). Например, у балки (рис. 7.2 а), которую далее будем называть заданной системой (ЗС), степень статической неопределимости n=1. Если исключить лишнюю связь (правую опору) и обозначить неизвестную реакцию через X, получим ее ОС (рис. 7.2 б).
Рис. 7.2 Способов исключения лишних связей очень много (теоретически – бесконечное число). Например, лишнюю связь можно исключать как на рис. 7.2 в-е. Однако одна из этих схем (рис. 7.2 е) геометрически изменяема и для дальнейшего расчета непригодна. Все остальные схемы могут быть приняты за основную систему. Если воспользоваться известным теоретическим положением о том, что в линейно-упругих системах внешняя нагрузка распределяется единственным образом, то результаты расчетов по различным ОС должны быть одинаковыми. Однако объем вычислений в разных ОС может быть разным. Поэтому из многих вариантов ОС нужно выбирать наиболее оптимальную. Например, в нашем примере первый вариант ОС (рис. 7.2 б) предпочтительнее остальных, т.к. в ней эпюры строятся легче. Итак, основная система должна быть: 1) обязательно геометрически неизменяемой; 2) простой для расчета; 3) учитывать особенности сооружения и действующей нагрузки. Сущность метода сил В рассматриваемом методе расчета статически неопределимых систем за основные неизвестные принимаются силы (внутренние усилия). Поэтому он и называется методом сил. Изучим метод сил на примере предыдущей балки (рис. 7.2 а). Потребуем, чтобы ее ЗС (рис. 7.2 а) и ОС (рис. 7.2 б) были эквивалентными. Для этого перемещение в направлении исключенной связи должно равняться нулю: D=0. По принципу суперпозиции, это перемещение равно сумме перемещения DX (рис. 7.3 а) от неизвестной реакции X и перемещения DP (рис. 7.3 б) от заданной силы P. Поэтому D=DX+DP=0. Это уравнение, учитывающее геометрические особенности системы, называется уравнениемсовместности деформаций.
Рис. 7.3 Так как сила X неизвестна, перемещение DX непосредственно определить нельзя. Поэтому рассмотрим единичное состояние (ЕС) основной системы, где действует только единичная сила P=1 (рис. 7.3 в). Перемещение d, возникающее в нем в направлении единичной силы, называется податливостью, и его уже можно определить. По закону Гука, в линейно-упругой системе DX=d X. Тогда последнее уравнение принимает вид
d X+DP=0. Его называют каноническим уравнением метода сил. Такое уравнение получается для любой один раз статически неопределимой системы. Если известны d и DP, из него определяется неизвестная сила: X= –DP/d. Если в системе имеется n лишних связей, то нужно исключить все эти лишние связи и выбрать ОС с n неизвестными X1, X2,..., Xn. Тогда, из условий эквивалентности ЗС и ее ОС (условий равенства нулю перемещений в направлениях исключенных связей) можно составить n уравнений совместности деформаций:
.............. Dn= При рассмотрении n различных единичных состояний системы и определении податливостей
.............
Она называется системой канонических уравнений метода сил. Здесь Систему с большим количеством уравнений необходимо решать на компьютере. С этой целью введем матричные обозначения:
где d – матрица податливости, X – вектор неизвестных, DP – вектор нагрузки, 0 – нуль-вектор. В результате этого система канонических уравнений принимает вид: d X + DP = 0. Из этого матричного уравнения определяется вектор неизвестных: X = – d –1 DP. Здесь d –1 – обратная матрица податливости.
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 560; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.140.108 (0.012 с.) |
 .
.
 –2nУ .
–2nУ .

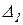 =
=  +
+ 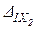 +×××+
+×××+ 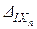 +D1P=0,
+D1P=0, =
=  +
+  +×××+
+×××+  +D2P=0,
+D2P=0, +
+  +×××+
+×××+  +DnP =0.
+DnP =0.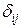 по различным направлениям эти уравнения приводятся к системе уравнений:
по различным направлениям эти уравнения приводятся к системе уравнений:
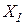 +
+ 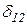 X2+×××+
X2+×××+  Xn+D
Xn+D  P=0,
P=0,
 X2+×××+
X2+×××+  Xn+D2P=0,
Xn+D2P=0,
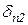 X2+×××+
X2+×××+  Xn+DnP=0.
Xn+DnP=0. – главные коэффициенты,
– главные коэффициенты,  d =
d = 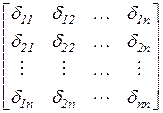 ; X =
; X =  ; DP =
; DP =  ; 0 =
; 0 =  ,
,


