Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы расчета статически определимых систем на постоянную нагрузку (продолжение)
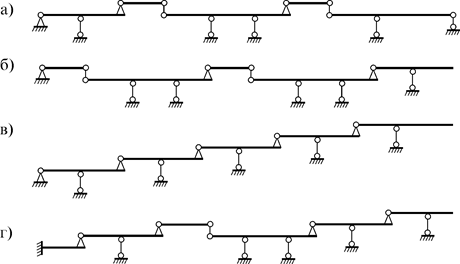
Расчет ферм Ферма – это геометрически неизменяемая система, состоящая из прямых стержней, соединенных в узлах жестко или шарнирно (рис. 4.1 а). Замена жестких узлов шарнирами превращает их в шарнирную ферму (рис. 4.1 б).
Рис. 4.1 Для статической определимости и геометрической неизменяемости шарнирных ферм должно выполняться условие
При действии узловой нагрузки стержни фермы работают в основном на растяжение или сжатие, а моменты и поперечные силы в них отсутствуют. Поэтому в стержнях шарнирной фермы определяются только продольные усилия. Положительное усилие Nij в стержне фермы между узлами i и j (рис. 4.2 а) следует направить в сторону от шарниров (рис. 4.2 б).
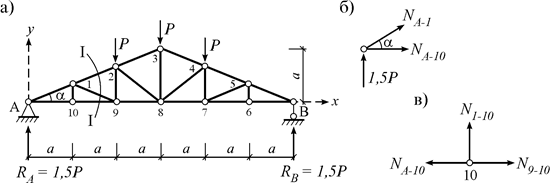
Рис. 4.2 При расчете простых ферм используются методы вырезания узлов, сквозных сечений, совместных сечений, замены стержней и др. Здесь рассмотрим только два метода. Метод вырезания узлов основан на последовательном вырезании и рассмотрении равновесия узлов фермы. Сущность метода: вырезается узел, в котором не более двух неизвестных; составляются уравнения равновесия SX = 0 и SY = 0; из них определяются неизвестные продольные усилия. После этого можно вырезать следующий узел и продолжить расчет. В методе вырезания узлов необходимо установить порядок вырезания узлов. Например, для расчета фермы (рис. 4.3 а) сначала вырежем узел A (рис. 4.3 б) и запишем уравнения равновесия: SX = NA-10+NA-1 cosa=0; SY = NA-1 sina+1,5P=0. Из них: NA-1= –1,5P/sina; NA-10=1,5P/tga.
Рис. 4.3 Теперь вырежем узел 10 (рис. 4.3 в) и запишем условия равновесия: SX = N9-10 –NA-10=0; SY = N1-10=0. Из них получаем: N9-10 =NA-10=1,5P/tga; N1-10=0. После этого можно вырезать узлы 1, 9, 2, 3, 8, 4, 7, 6, 5. У метода вырезания узлов есть недостаток: ошибка (неточность), допущенная при расчете одного узла, влияет на последующие вычисления. Поэтому результаты, полученные этим методом, надо контролировать. Например, результаты расчета фермы могут быть проверены по формуле
где Из метода вырезания узлов вытекают несколько признаков (частных случаев), упрощающих расчет ферм: 1) если в узле сходятся два стержня и внешняя нагрузка не приложена (рис. 4.4 а), то оба усилия равны нулю: N1 = N2 = 0; 2) если в узле сходятся два стержня, а внешняя нагрузка действует в направлении одного стержня (рис. 4.4 б), то N1 = P, N2 = 0;
3) если в трехстержневом узле два стержня лежат на одной прямой, а внешней нагрузки нет (рис. 4.4 в), то усилия в двух стержнях равны: N1 = N2, а усилие в боковом стержне равно нулю: N3 = 0; 4) если в четырехстержневом узле стержни попарно лежат на одной прямой, а внешней нагрузки нет (рис. 4.4 г), то усилия также попарно равны между собой: N1 = N2, N3 = N4.
Рис. 4.4 Используя эти признаки легко определяются некоторые усилия рассмотренной фермы (рис. 4.3 а): – по 2-му признаку N1-10=N1-9=N2-9=0; N5-6=N5-7=N4-7=0; – по 3-му признаку NA-10=N9-10=N8-9; NB-6=N6-7=N7-8; NA-1=N1-2; NB-5= N4-5. Метод сквозных сечений позволяет определять усилие в стержне фермы только из одного уравнения. Сущность метода: поперек фермы проводится такое сквозное сечение, чтобы появилось не более трех неизвестных усилий; в точке пересечения направлений двух из них составляется уравнение момента, из которого определяется третье усилие. Точка, в которой составляется уравнение момента, называется моментной точкой.
SM1 = N9-10× Отсюда получаем: N9-10=4,5P. Рис. 4.5 Точка 9 является моментной точкой для N1-2. Поэтому SM9 = –N1-2 b –1,5P×2a=0. Так как b=2a×sina, получаем N1-2=–1,5P/ sina. Для N1-9: SMA = – N1-9×c=0. Отсюда получаем N1-9=0. Иногда (например, когда два стержня параллельны) моментной точки не существует. В этом случае вместо уравнения момента следует составлять уравнение проекции на ось, перпендикулярную этим параллельным стержням. У метода сквозных сечений есть один недостаток: в сложных фермах не удается провести такое сквозное сечение, чтобы появились только три неизвестных усилия. В этом случае некоторые неизвестные нужно определять заранее или использовать другие методы (методы совместных сечений или замены связей). Расчет разрезных балок В зависимости от расположения опор и шарниров, разрезные балки могут быть разными (рис. 4.6).
Рис. 4.6 Для геометрической неизменяемости и статической определимости разрезных балок должно выполняться условие
Взаимодействие частей разрезной балки легче изучать путем составления их этажных схем. Для этого выявляются те части балки, которые могут самостоятельно нести внешнюю нагрузку (назовем их главными балками). Все главные балки изображаются на нижнем этаже. Те части балки, которые примыкают к главным балкам (подвесные балки) и могут нести нагрузку только при опирании на главные балки, изображаются этажом выше и т.д. В результате получается этажная схема балки. Например, рассмотренные на рис. 4.6 разрезные балки можно представить в виде следующих этажных схем (рис. 4.7).
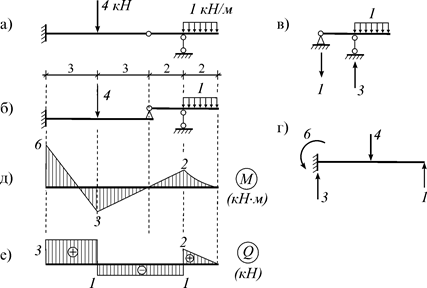
Рис. 4.7 Расчет разрезных балок начинается с самого верхнего этажа: определяются опорные реакции и внутренние усилия этой части балки от ее нагрузки. После этого переходим к нижележащему этажу. Однако, кроме своей нагрузки, к нему следует приложить и давление от вышележащего этажа (которое равно реакции вышележащего этажа, но направлено в противоположную сторону). Затем определяются его реакции и внутренние усилия. Далее расчет продолжается до самого нижнего этажа. Рассмотрим пример (рис. 4.8 а). Вначале строим этажную схему (рис. 4.8 б), проводим расчет подвесной балки (рис. 4.8 в), а затем главной балки (рис. 4.8 г). Полученные эпюры для отдельных частей балки объединяем в общие эпюры M и Q (рис. 4.8 д, е).
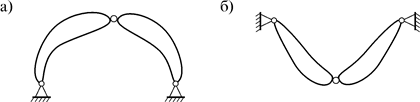
Рис. 4.8 Расчет трехшарнирных систем Трехшарнирная система – это система из двух дисков, связанных между собой и основанием тремя шарнирами. Есть трехшарнирные системы двух видов: арочные (рис. 4.9 а) и подвесные системы (рис. 4.9 б).
Рис. 4.9 Их расчет мало отличается друг от друга. Поэтому остановимся на арочных системах, которые бывают трех типов: трехшарнирные рамы (рис. 4.10 а), трехшарнирные арочные фермы (рис. 4.10 б) и трехшарнирные арки (рис. 4.10 в):
Рис. 4.10 Особенность трехшарнирных систем состоит в том, что в них возникает распор (боковое давление) даже от вертикальной нагрузки. Опорные реакции таких систем (рис. 4.11 а) можно определять методом совместных сечений. В результате появляются независимые две части с шестью неизвестными (четыре опорные реакции RA, RB, HA, HB и две междисковые реакции XC, YC (рис. 4.11 б).
Рис. 4.11 Составив для каждого диска по три уравнения равновесия (всего шесть уравнений), можно определить все эти реакции. Далее каждый диск рассчитывается самостоятельно. В о п р о с ы 1. Какие упрощения принимаются при расчете ферм? 2. Какие методы используются при расчете ферм? 3. Какова сущность метода сквозных сечений? 4. Назовите признаки, упрощающие расчет ферм. 5. Как строится этажная схема? 6. В чем главная особенность трехшарнирных систем? Л е к ц и я 5 РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ НА ПОДВИЖНУЮ НАГРУЗКУ Подвижной нагрузкой называется нагрузка, движущаяся по сооружению с некоторой скоростью. К примеру, такой нагрузкой является транспорт (рис. 5.1 а). Его можно рассматривать как систему взаимо-связанных параллельных сил, движущихся по сооружению (рис. 1.5 б).
Рис. 5.1
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.240.243 (0.024 с.) |

 .
.
 ,
, – усилия в стержнях,
– усилия в стержнях,  – длины стержней,
– длины стержней,  и
и  – проекции нагрузок (включая и опорные реакции), x и y – координаты нагрузок.
– проекции нагрузок (включая и опорные реакции), x и y – координаты нагрузок.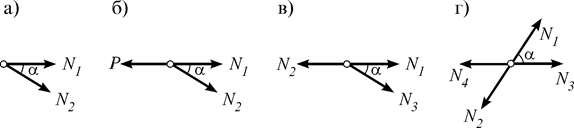
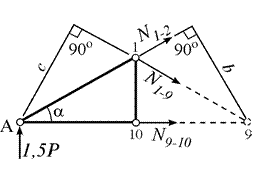 В качестве примера рассмотрим ту же ферму, проведя через нее сквозное сечение I–I (рис. 4.3 а). Рассматривая равновесие левой части от сечения (рис. 4.5), составим уравнение момента в точке 1:
В качестве примера рассмотрим ту же ферму, проведя через нее сквозное сечение I–I (рис. 4.3 а). Рассматривая равновесие левой части от сечения (рис. 4.5), составим уравнение момента в точке 1: –1,5P×a=0.
–1,5P×a=0.
 .
.