
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутренние усилия стержневой системы
В элементах плоской стержневой системы возникают три усилия: продольная сила N, поперечная сила Q, изгибающий момент M. Для любого поперечного сечения стержня они определяются как на рис. 3.1.
Рис. 3.1 Изгибающий момент – это сумма моментов всех сил, лежащих слева (или справа) от сечения относительно оси z:
В строительной механике знак изгибающего момента обычно не уста-навливается, а эпюра M изображается на стороне растянутого волокна. Поперечная сила – это сумма проекций на ось y всех сил, лежащих слева (или справа) от сечения:
Поперечная сила положительна, если вращает элемент по часовой стрелке, и отрицательна, если вращает его против часовой стрелки. Продольная сила – это сумма проекций всех сил на ось x, лежащих слева (или справа) от сечения:
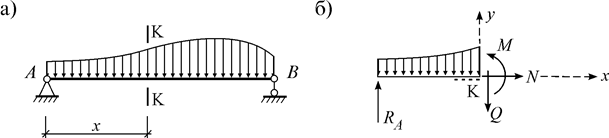
Продольная сила положительна, если растягивает элемент, и отрицательна, если сжимает его. Между M и Q существует дифференциальная зависимость: Q= Исходя из геометрического смысла первой производной, величина Q равняется тангенсу угла между осью эпюры M и касательной к ней. По эпюре M можно определить знак Q. Для этого ось эпюры M нужно повернуть до совпадения с касательной к ней. Если поворот будет по часовой стрелке, Q будет со знаком «+», а если против часовой стрелки, то со знаком «–». Эпюры поперечных и продольных сил можно изображать на любой стороне от оси стержня, но эпюру изгибающего момента нужно обязательно изображать на стороне растянутого волокна. 3. Методы определения внутренних усилий Внутренние усилия статически определимых систем определяются методами простых сечений, совместных сечений, вырезания узла, замены связей и др. Метод простых сечений Этот метод позволяет рассматривать внутреннее усилие как внешнюю силу и определять его из уравнений статики (равновесия). Например, внутренние усилия балки (рис. 3.2 а) в сечении К определяются как на рис. 3.2 б.
Рис. 3.2 Алгоритм метода простых сечений: 1) поделить систему на участки; 2) выбрать участок и провести поперечное сечение; 3) выбрать одну (наиболее простую) из отсеченных частей; 4) составить три уравнения равновесия; 5) из них определить внутренние усилия M, Q, N; 6) для данного участка построить эпюры M, Q, N; 7) повторить пункты 2-6 для остальных участков.
Метод совместных сечений Этот метод используется при расчете многодисковых систем. Например, для расчета трехдисковой рамы (рис. 3.3 а) проводятся три совместных сечения I, II, III. В результате выявляются девять неизвестных реакций (рис. 3.3 б): опорные реакции R1, R2, H и междисковые реакции X1, X2, X3, Y1, Y2, Y3. Составив для каждого диска по три уравнения равновесия, т.е. 3´3=9 уравнений, из их решения определяются все 9 реакций.
Рис. 3.3 Алгоритм метода совместных сечений: 1) совместными сечениями разделить систему на части (диски); 2) обозначить опорные и междисковые реакции; 3) для каждого диска записать уравнения равновесия; 4) решить систему полученных уравнений; 5) каждый диск рассчитать отдельно и построить эпюры; 6) объединить все эпюры в общие эпюры M, Q, N. Метод вырезания узла Используется для определения усилий простых систем. Сущность метода: вырезается узел с не более чем двумя неизвестными усилиями; силы, действующие в узле, проецируются на две оси; из этих уравнений определяются искомые усилия. Например, при расчете балочно-ферменной системы (рис. 3.4 а), после того как определены опорные реакции (рис. 3.4 б), вырезается узел А (рис. 3.4 в) и составляются уравнения равновесия: SX = N2 cos45– N1 cos45= 0, SY = N1 sin45+ N2 sin45+ P/2 = 0. Из них определяются искомые продольные силы:
Рис. 3.4 Метод замены связей Используется при расчете сложных статически определимых систем, которые трудно рассчитать другими способами. Сущность метода: сложная система превращается в более простую путем перестановки связи (или нескольких связей) в другое место; из условия эквивалентности заданной и заменяющей систем определяется усилие в переставленной связи; затем система рассчитывается известными способами. Например, для расчета рамы (рис. 3.5 а) удалим правый вертикальный стержень заданной системы (ЗС) и введем одну связь в левый шарнир. Тогда шарнир станет припайкой С, а примыкающие к нему стержни будут жестко связаны. Обозначив усилие в удаленной связи через X, получим так называемую основную систему (ОС) для расчета рамы (рис. 3.5 б).
Рис. 3.5 Условием эквивалентности ОС по отношению к ЗС будет условие равенства нулю момента в точке С: MC=0. По принципу суперпозиции этот момент равняется сумме моментов от силы X и внешней нагрузки:
MC=MC,X + MC,P =0. Теперь рассмотрим два состояния ОС: 1) единичное состояние (ЕС), где прикладываются силы X=1 (рис. 3.5 в); 2) грузовое состояние (ГС), где прикладывается нагрузка (рис. 3.5 г). Тогда предыдущее уравнение примет вид
где MC,P= Теперь неизвестное усилие легко вычисляется:
После этого можно перейти к расчету более простой системы (рис. 3.5 д). В более сложных случаях переставляются несколько связей и записываются столько же условий эквивалентности: s11X1+s12X2+¼+ s1nXn+S1P=0, s21X1+s22X2+¼+ s2nXn+S2P=0,................. sn1X1+sn2X2+¼+ snnXn+SnP=0. Здесь 1, 2, ¼, n – заменяемые связи; X1, X2, ¼, Xn – неизвестные внутренние усилия в этих связях; sij – усилие в связи i в j- ом единичном состоянии; SiP – усилие в i- ой связи в грузовом состоянии. Из этой системы уравнений определяются неизвестные X1, X2, ¼, Xn. Общий вывод. Расчет любой статически определимой системы приводит к решению системы n линейных уравнений с n неизвестными. Если определитель полученной системы уравнений отличен от нуля (det¹0), внутренние усилия будут конечными величинами. Если же определитель равняется нулю (det=0), то внутренние усилия определить нельзя. В этом случае система является мгновенно изменяемой. В о п р о с ы 1. Какая система называется статически определимой? 2. Какие особенности имеет статически определимая система? 3. Какие формы уравнений равновесия можно записать для плоской системы? 4. Что такое изгибающий момент, поперечная сила и продольная сила, как определяются их знаки? 5. Какие методы используются при расчете статически определимых систем? 6. В чем сущность метода замены связей? 7. Какой общий вывод можно сделать после анализа методов расчета статически определимых систем? Л е к ц и я 4
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.53.209 (0.012 с.) |

 .
. .
. .
.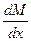 .
.

 .
.


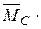 X + MC,P =0,
X + MC,P =0, =1×a=a – момент в точке С в единичном состоянии;
=1×a=a – момент в точке С в единичном состоянии; – момент в точке С в грузовом состоянии.
– момент в точке С в грузовом состоянии. .
.


