
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет статически неопределимых систем методом сил (продолжение)Содержание книги
Поиск на нашем сайте
Проверка правильности коэффициентов При вычислении коэффициентов системы канонических уравнений возможны ошибки. Поэтому их надо проверять. Существует три способа проверки коэффициентов. 1. Построчная проверка проводится для проверки всех коэффициентов одного уравнения. Если сложить все коэффициенты при неизвестных i -го уравнения, то
= Здесь: Отсюда следует, что если сумма всех коэффициентов i-ой строки системы канонических уравнений равна произведению i-ой единичной эпюры на суммарную единичную эпюру, т.е.
то коэффициенты этой строки вычислены верно. 2. Универсальная проверка используется для одновременной проверки всех коэффициентов системы канонических уравнений. Приведем (без доказательства) только общее правило этой проверки: если сумма всех коэффициентов системы канонических уравнений равна произведению суммарной единичной эпюры на себя, т.е.
то все коэффициенты системы канонических уравнений вычислены верно. 3. Постолбцовая проверка используется для проверки коэффициентов одного столбца системы канонических уравнений. Приведем правило проверки столбца из грузовых коэффициентов: если сумма всех грузовых коэффициентов равна произведению суммарной единичной эпюры на грузовую эпюру, т.е.
то грузовые коэффициенты вычислены верно. Определение внутренних усилий После подсчета и проверки коэффициентов системы канонических уравнений все они подставляются в эти уравнения, а потом система уравнений решается относительно неизвестных X1, X2, …, Xn. Затем определяются внутренние усилия заданной статически неопределимой системы. Эту задачу можно решить двумя способами: 1) подстановкой найденных величин X1, X2, …, Xn в основную систему и определением ее усилий M, Q, N; 2) используя эпюры внутренних усилий в единичных состояниях M= При расчете рам и балок обычно используется только первая из этих формул, и по ней строится эпюра изгибающих моментов M. Эпюра Q строится по эпюре M с дифференциальной зависимости, а эпюра N строится по эпюре Q способом вырезания узлов. Алгоритм метода сил Порядок расчета рамы методом сил состоит из следующих этапов: 1. Определение степени статической неопределимости. 2. Выбор основной системы. 3. Запись канонических уравнений. 4. Рассмотрение единичных и грузового состояний. 5. Построение единичных и грузовой эпюр. 6. Определение коэффициентов канонических уравнений. 7. Решение системы канонических уравнений. 8. Построение эпюр M, Q, N. 9. Проверка правильности расчета. Она состоит их двух частей: 1) статическая проверка состоит в проверке выполнения условий равновесия; 2) кинематическая проверка состоит в проверке всех условий Действительно,
А это выражение равно нулю, так как является i -ой строкой системы канонических уравнений. Отсюда следует, что
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.31.90 (0.006 с.) |

 =
= 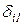 +
+ 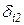 + … +
+ … +  =
= 
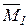 +
+ 
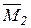 + … +
+ … + 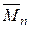 =
= )=
)= 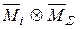 =
= 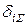 .
.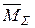 =
= 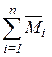 =
= 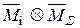 ,
,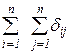 =
= 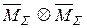 =
= 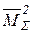 ,
,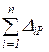 =
= 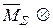
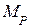 ,
,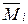 ,
, 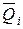 ,
, 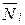 и в грузовом состоянии MP, Q P, NP с учетом закона Гука и принципа суперпозиции; в этом случае внутренние усилия определяются по формулам:
и в грузовом состоянии MP, Q P, NP с учетом закона Гука и принципа суперпозиции; в этом случае внутренние усилия определяются по формулам: X1+
X1+ 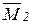 X2+ …+
X2+ …+ 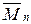 Xn+MP; Q=
Xn+MP; Q= 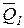 X1+
X1+  X2+ …+
X2+ …+ 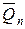 Xn+QP ; N=
Xn+QP ; N= 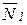 X1+
X1+ 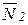 X2+ …+
X2+ …+  Xn+NP .
Xn+NP . =0 (
=0 (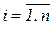 ) или общего условия
) или общего условия 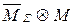 =0.
=0.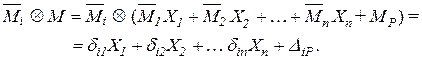
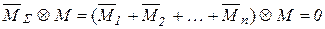 , поскольку каждый из его сомножителей равняется нулю.
, поскольку каждый из его сомножителей равняется нулю.


