
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет статически неопределимых систем методом перемещений (продолжение)
Элементарные состояния основной системы Как было установлено в предыдущей лекции, коэффициенты системы канонических уравнений метода перемещений – реакции, определяемые в единичных и грузовом состояниях. Например, Все эти реакции равны сумме реакций отдельных стержней, объединяемых в узлах основной системы. Для их определения необходимо рассчитывать статически неопределимые стержни различной длины и жесткости с различными закреплениями по концам, получающие разные перемещения или нагруженные различными силами. С целью упрощения таких расчетов все типовые задачи, встречающиеся при расчете различных основных систем, решаются для общего случая. Их называют элементарными состояниями основной системы, а результаты их расчетов сводятся в таблицу. Эти задачи в большинстве случаев бывают статически неопределимыми и поэтому решаются методом сил. Рассмотрим решение двух типовых задач. Стержень с равномерно распределенной нагрузкой q Степень статической неопределимости этой системы (рис. 11.1 а) n=1. Каноническое уравнение имеет вид
Рис. 11.1 Определим коэффициенты канонического уравнения:
а затем неизвестную реакцию: Поворот одного конца стержня с заделанными концами Пусть один конец стержня с заделанными концами поворачивается на единичный угол (рис. 11.2 а). У этой системы степень статической неопределимости n=3. Однако, если не учитывать продольную деформацию, вместо заданной системы можно рассматривать стержень с правой опорой в виде ползуна (рис. 11.2 б) и принять n=2.
Рис. 11.2 Система канонических уравнений будет:
Если основную систему выбрать симметричной (рис. 11.2 в), в обоих единичных состояниях (рис. 11.2 г, е) единичные эпюры Определим коэффициенты канонических уравнений:
Из рис. 11.2 з следует что Так как Аналогичные расчеты проводятся для всех типовых случаев, встречающихся в различных основных системах. Результаты их расчетов сводятся в единую таблицу метода перемещений.
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.153 (0.005 с.) |
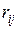 – реакция, возникающая в i -ой связи в j -ом единичном состоянии,
– реакция, возникающая в i -ой связи в j -ом единичном состоянии, 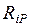 – реакция, возникающая в i -ой связи в грузовом состоянии.
– реакция, возникающая в i -ой связи в грузовом состоянии.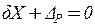 . Выбирая основную систему (рис. 11.1 б), в единичном (рис. 11.1 в) и грузовом (рис. 11.1 д) состояниях строим единичную (рис. 11.1 г) и грузовую эпюры (рис. 11.1 е).
. Выбирая основную систему (рис. 11.1 б), в единичном (рис. 11.1 в) и грузовом (рис. 11.1 д) состояниях строим единичную (рис. 11.1 г) и грузовую эпюры (рис. 11.1 е).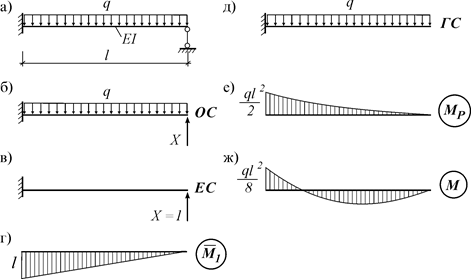
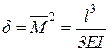 ,
, 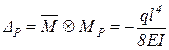 ,
,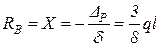 . После этого из уравнений статики определяем остальные реакции, а по формуле
. После этого из уравнений статики определяем остальные реакции, а по формуле 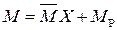 строим эпюру изгибающих моментов (рис. 11.1 ж).
строим эпюру изгибающих моментов (рис. 11.1 ж).
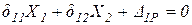 ,
,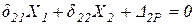 .
. ,
, 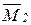 легко строятся (рис. 11.2 д, ж). В грузовом состоянии (рис. 11.2 з) момент не возникает, поэтому
легко строятся (рис. 11.2 д, ж). В грузовом состоянии (рис. 11.2 з) момент не возникает, поэтому 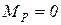 .
.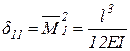 ,
, 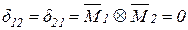 ,
, 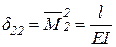 .
.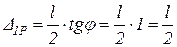 и
и 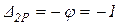 , а из канонических уравнений получаем
, а из канонических уравнений получаем 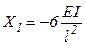 ,
, 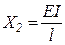 .
.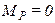 , имеем
, имеем 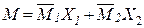 (рис. 11.2 и).
(рис. 11.2 и).


