
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линии влияния поперечной силы и момента
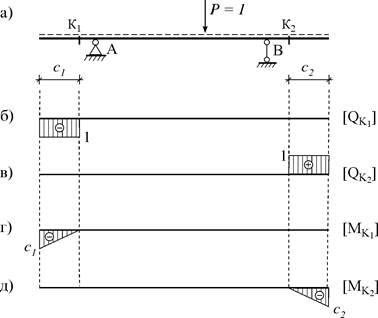
Они зависят от положения сечения, в котором определяются. а) Единичная сила правее сечения К В этом случае QK= RA, MK= RA×a. Эти функции определяют правые ветвиЛВ поперечной силы и момента в сечении К (рис. 5.2 г, д). б) Единичная сила левее сечения К В этом случае внутренние усилия определяем через правую опорную реакцию. Тогда QK=– RB, MK=RB×b. Эти функции определяют левые ветви ЛВ поперечной силы и момента в сечении К (рис. 5.2 г, д). Если сечение располагается на консольных (левой или правой) частях балки (рис. 5.3 а), ЛВ поперечной силы и момента будут совсем другими. Приведем результат их построения для двух сечений К1 и К2 (рис. 5.3 б-д).
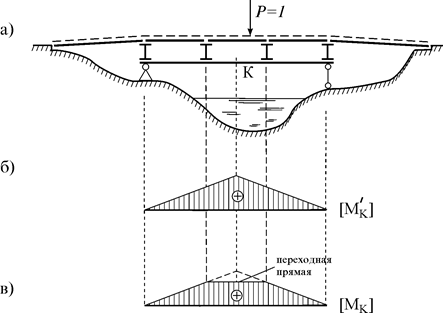
Рис. 5.3 В некоторых расчетных схемах (например, в этажных схемах разрезной балки) встречаются консоли с заделками справа или слева. ЛВ их усилий можно получить и без расчетов, используя соответствующие левые и правые части предыдущих линий влияния (рис. 5.3 б-д), считая, что в точках А и В имеются заделки. Полученные ЛВ опорных реакций и внутренних усилий используются как известные решения при расчете аналогичных балок и как промежуточные решения при расчете многопролетных балок. Построение ЛВ при узловой передаче нагрузки В некоторых сооружениях нагрузка на их несущую часть может передаваться через вспомогательные балки. Например, такая конструктивная схема часто используется в мостах: там на главную балку накладываются поперечные балки, а на них – настил (рис. 5.4 а). В таких сооружениях нагрузка на главные балки передается через узлы пересечения главной балки с поперечными балками.
Рис. 5.4 Если бы нагрузка действовала только на главную балку, ЛВ момента MK была бы как на рис. 5.4 б. Поэтому, когда единичная сила находится над поперечными балками, ординаты ЛВ будут такими же. Но, когда единичная сила находится между поперечными балками, ЛВ сглаживается (рис. 5.4 в).
Определение усилий по ЛВ Пусть ЛВ какого-то усилия S определяется уравнением y=f(x). По этому графику можно определять усилие S от произвольной нагрузки.
S=S Pi yi. Действие распределенной нагруз-ки (рис. 5.5 б). Если рассматривать элементарную силу q(x)dx как сосредоточенную силу, то Рис. 5.5 S= Когда же распределенная нагрузка постоянна, т.е. q(x)=q=const, то S=q Здесь w – площадь ЛВ в области действия распределенной нагрузки. Если на сооружение действует несколько сосредоточенных сил и распределенных нагрузок, то по принципу суперпозиции S=S Pi yi+S qj ωj. Построение ЛВ усилий фермы Рассмотрим ферму (рис. 5.6 а). При воздействии только вертикальной нагрузки ее опорные реакции будут такими же как у вспомогательной балки (рис. 5.6 б). Поэтому ЛВ опорных реакций фермы будут аналогичны ЛВ балки (рис. 5.6 в, г). Для построения ЛВ продольных усилий фермы воспользуемся способами вырезания узлов и сквозных сечений. а) Использование способа вырезания узлов Для построения ЛВ N2-6 вначале рассмотрим узел 1. Так как к этому узлу силы не приложены, то по признаку 1 N1-6=0. После этого вырежем узел 6 фермы. Здесь могут быть два случая: 1) когда единичная сила P=1 находится в этом узле (рис. 5.6 е), то SY= N2-6 sina+1–1=0. Отсюда N2-6=0. 2) когда единичная сила P=1 находится вне этого узла (рис. 5.6 ж), то SY=N2-6 sina+RA=0. Отсюда N2-6= – Тогда, используя ЛВ опорной реакции RA, можно построить ЛВ усилия N2-6 (рис. 5.6 д).
Рис. 5.6 б) Использование способа сквозных сечений Поперек фермы проведем сквозное сечение I–I (рис. 5.7 а) и получим независимые левые и правые части. Единичная сила P=1 может находиться в обоих частях фермы. 1)Единичная сила левее сечения(рис. 5.7 б): SM SY 2)Единичная сила правее сечения (рис. 5.7 в): SM SY В первом случае определяем ординаты ЛВ этих усилий между узлами 6-7, т.е. определяем их левые ветви, а во втором случае определяем ординаты обоих ЛВ между узлами 8-10, т.е. определяем правые ветви ЛВ. Соединив точки между узлами 7-8, получаем переходную прямую и окончательный вид ЛВ (рис. 5.7 г, д).
Рис. 5.7 Как видно из этих примеров, у ЛВ продольных усилий фермы есть следующее свойства: ветви ЛВ пересекаются под моментной точкой; если же моментной точки нет, ветви ЛВ параллельны.
В о п р о с ы 1. Что такое линия влияния и чем она отличается от эпюры? 2. В чем преимущество метода линий влияния? 3. Чем отличается ЛВ при узловой передаче нагрузки? 4. Как определяется усилие от постоянной нагрузки по ЛВ? 5. Какие способы используются при построении ЛВ усилий фермы? Л е к ц и я 6 ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ Понятие о перемещениях При воздействии нагрузки, температуры и других факторов сооружения меняют свою форму, а его точки получают перемещения. Перемещение – векторная величина. Перемещение любой точки на плоскости можно задать через его модуль и направление. Например, вектор перемещения DA= Поступательные перемещения DA, DxA, DyA будем называть линейными перемещениями, а jA – угловым перемещением.
Рис. 6.1 Методы определения перемещений основаны на определении работ внешних и внутренних сил. В механике рассматриваются два вида таких работ – действительные и возможные работы.
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.160.219 (0.01 с.) |
 Действие сосредоточенной силы (рис. 5.5 а). Если система упругая, то внутреннее усилие прямо пропор-ционально нагрузке. Поэтому S=Py. Если же действует несколько сил, то внутреннее усилие определяется по принципу суперпозиции:
Действие сосредоточенной силы (рис. 5.5 а). Если система упругая, то внутреннее усилие прямо пропор-ционально нагрузке. Поэтому S=Py. Если же действует несколько сил, то внутреннее усилие определяется по принципу суперпозиции: .
. .
.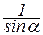 ×RA.
×RA.
 =N2-3 h+RB 2a=0. Отсюда N2-3= –2
=N2-3 h+RB 2a=0. Отсюда N2-3= –2 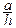 RB ;
RB ; = –N3-7 sin a +RB=0. Отсюда N3-7=
= –N3-7 sin a +RB=0. Отсюда N3-7= 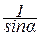 RB .
RB . = –N2-3 h – RA a=0. Отсюда N2-3= –
= –N2-3 h – RA a=0. Отсюда N2-3= –  =N3-7 sina+RA=0. Отсюда N3-7= –
=N3-7 sina+RA=0. Отсюда N3-7= – 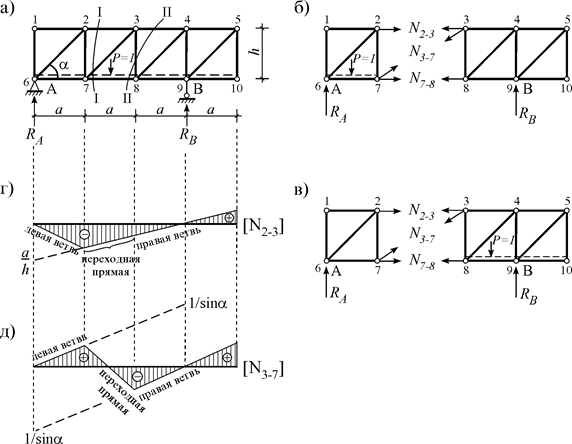
 точки А рамы в точку А¢ (рис. 6.1 а) определяется через его модуль DA и угол (направление) jA (рис. 6.1 б). А эти величины можно определять через горизонтальную и вертикальную составляющие DxA и DyA вектора перемещения
точки А рамы в точку А¢ (рис. 6.1 а) определяется через его модуль DA и угол (направление) jA (рис. 6.1 б). А эти величины можно определять через горизонтальную и вертикальную составляющие DxA и DyA вектора перемещения  :
: , jA=arc tg
, jA=arc tg  .
.



